Capitolo 4 Analisi delle Componenti Principali (PCA) e Analisi Fattoriale Esplorativa (EFA)
4.1 Introduzione
Quando ci troviamo ad operare in situazioni in cui si hanno dati con un gran numero di dimensioni, è naturale pensare di proiettare questi dati in un sottospazio di dimensionalità inferiore, cercando contestualmente di non perdere informazione importante sulle variabili originarie. Un modo per ottenere tale riduzione è attraverso la selezione delle variabili, chiamata anche “feature selection”. Un altro modo è tramite la creazione di un insieme ridotto di trasformazioni lineari o non lineari delle variabili di input. La creazione di queste variabili (o “feature”) composite, tramite tecniche di proiezione, è spesso indicata col termine di “feature extraction”.
L’Analisi delle Componenti Principali (PCA) e l’Analisi Fattoriale (FA) sono tecniche finalizzate a ridurre la dimensionalità di un insieme di dati con finalità esplorative, di visualizzazione dei dati o feature extraction, per un eventuale uso in analisi successive.
4.2 PCA
L’analisi delle componenti principali (PCA) è una tecnica finalizzata a derivare, a partire da un set di variabili numeriche correlate, un insieme più ridotto di variabili ortogonali “artificiali”. L’insieme ridotto di proiezioni ortogonali lineari (noto come “componenti principali” o “principal components”, “PC”) è ottenuto combinando linearmente in maniera appropriata le variabili originarie.
In PCA, si indica col termine “informazione” la variabilità totale delle variabili di input originarie, cioè la somma delle varianze delle variabili originarie. Punto centrale della PCA è la cosiddetta scomposizione spettrale (chiamata anche scomposizione in autovalori e autovettori, o eigendecomposition) della matrice di varianze/covarianze campionaria. Questa scomposizione ritorna gli autovalori e autovalori della matrice di covarianze. Gli autovalori (in ordine decrescente di valore) rappresentano l’ammontare della variabilità totale osservata sulle variabili originarie, “spiegata” (o “espressa”) da ciascuna componente principale; gli autovettori invece rappresentano le corrispondenti direzioni (ortogonali) di massima variabilità estratte dalle componenti principali.
L’auspicio nell’applicazione della PCA è che le varianze campionarie delle prime Componenti Principali (PC) siano grandi, mentre le varianze delle altre componenti siano abbastanza piccole da poterne considerare trascurabili le corrispondenti PC. Una variabile, tra le componenti principali, che abbia una scarsa variabilità (relativamente alle altre variabili) può essere trattata approssimativamente come una costante. Omettere PC a bassa variabilità campionaria e porre tutta l’attenzione sulle PC con varianza più elevata, può essere visto come un modo semplice e “sensato” di ridurre la dimensionalità (numero di colonne) del dataset.
Dato un insieme di dati multivariati in cui le variabili hanno tipo e origine completamente differenti, si ha che la struttura delle componenti principali derivate dalla matrice di covarianze dipenderà dalla scelta essenzialmente arbitraria delle unità di misura. Inoltre, se ci sono grandi differenze tra le varianze delle variabili originarie, allora le variabili originarie con varianza più elevata tenderanno a dominare nelle componenti principali più importanti. Pertanto, usualmente le componenti principali dovrebbero essere estratte dalla matrice di covarianze solo quando tutte le variabili originarie si dovessero “muovere” approssimativamente sulla stessa scala. Poiché però questo fatto è usualmente raro, nella pratica le componenti principali sono estratte dalla matrice di correlazione delle variabili, che equivale a calcolare le componenti pricipali dalle variabili originarie dopo che ciascuna di esse è stata standardizzata in maniera da avere varianza unitaria. Questo usualmente si suggerisce per avere le variabili originarie “ugualmente importanti” nell’analisi delle componenti principali.
In R ci sono molte funzioni per calcolare le componenti principali. Quelle principali disponibili in
R base sono princomp() e prcomp(). La prima usa la scomposizione diretta in autovalori/autovettori
per ottenere le componenti principali; la seconda usa la scomposizione in valori singolari
o singular value decomposition (SVD). SVD è generalmente il metodo preferito per l’accuratezza numerica.
princomp() inoltre usa \(n\) (la dimensione del campione) come divisore per il calcolo delle varianze
campionarie, mentre prcomp() usa il più usuale \((n - 1)\).
Ovviamente, quando si esegue la PCA su matrici di correlazione il divisore non impatta in alcun modo
sui risultati
4.2.1 Esempio: Dati di vita attesa
Consideriamo il dataset life. Questo dataset contiene i valori di vita attesa nel 1960, alla nascita, a 25, 50 e 75 anni di età per uomini (men) e donne (women) in 31 paesi o regioni del mondo.
## Classes 'tbl_df', 'tbl' and 'data.frame': 31 obs. of 9 variables:
## $ country: chr "Algeria" "Cameroon" "Madagascar" "Mauritius" ...
## $ m0 : num 63 34 38 59 56 62 50 65 56 69 ...
## $ m25 : num 51 29 30 42 38 44 39 44 46 47 ...
## $ m50 : num 30 13 17 20 18 24 20 22 24 24 ...
## $ m75 : num 13 5 7 6 7 7 7 7 11 8 ...
## $ w0 : num 67 38 38 64 62 69 55 72 63 75 ...
## $ w25 : num 54 32 34 46 46 50 43 50 54 53 ...
## $ w50 : num 34 17 20 25 25 28 23 27 33 29 ...
## $ w75 : num 15 6 7 8 10 14 8 9 19 10 ...## country m0 m25 m50
## Length:31 Min. :34.00 Min. :29.00 Min. :13.00
## Class :character 1st Qu.:57.50 1st Qu.:42.50 1st Qu.:21.50
## Mode :character Median :61.00 Median :44.00 Median :23.00
## Mean :59.61 Mean :43.48 Mean :22.94
## 3rd Qu.:65.00 3rd Qu.:46.00 3rd Qu.:24.00
## Max. :69.00 Max. :51.00 Max. :30.00
## m75 w0 w25 w50 w75
## Min. : 5.000 Min. :38.00 Min. :32.00 Min. :17.00 Min. : 6.00
## 1st Qu.: 7.000 1st Qu.:62.00 1st Qu.:46.00 1st Qu.:25.00 1st Qu.: 8.50
## Median : 8.000 Median :66.00 Median :49.00 Median :27.00 Median :10.00
## Mean : 8.387 Mean :64.19 Mean :47.52 Mean :26.29 Mean :10.13
## 3rd Qu.: 9.000 3rd Qu.:68.00 3rd Qu.:51.00 3rd Qu.:28.00 3rd Qu.:11.00
## Max. :14.000 Max. :75.00 Max. :54.00 Max. :34.00 Max. :19.00Useremo solo le ultime otto variabili del data frame perché la prima (country) è una variabile di testo e quindi non può essere usata nella PCA. Useremo tuttavia questa variabile per rappresentare graficamente i risultati.

Come si vede dalla matrice di scatterplot qui sopra, alcune variabili originarie
sono correlate; potrebbe quindi essere utile pre-elaborare i dati usando la
PCA. Per evitare che la variabilità delle singole variabili possa influenzare i risultati,
standardizzeremo prima le variabili stesse. Questo può essere fatto specificando gli argomenti
opzionali cor = TRUE e scale = TRUE nelle funzioni princomp() e prcomp(), rispettivamente.
Come detto, questo corrisponde ad eseguire la PCA sulla matrice di correlazione delle variabili
originarie:
## user system elapsed
## 0.002 0.000 0.002## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 13.5934012 4.5370290 2.4515180 1.191561472 0.764224458
## Proportion of Variance 0.8620605 0.0960339 0.0280383 0.006623909 0.002724729
## Cumulative Proportion 0.8620605 0.9580944 0.9861327 0.992756588 0.995481317
## Comp.6 Comp.7 Comp.8
## Standard deviation 0.648841377 0.593016147 0.4426119310
## Proportion of Variance 0.001964077 0.001640645 0.0009139611
## Cumulative Proportion 0.997445394 0.999086039 1.0000000000## user system elapsed
## 0.001 0.000 0.001## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 13.8181 4.61203 2.49204 1.21126 0.77686 0.65957 0.60282
## Proportion of Variance 0.8621 0.09603 0.02804 0.00662 0.00272 0.00196 0.00164
## Cumulative Proportion 0.8621 0.95809 0.98613 0.99276 0.99548 0.99745 0.99909
## PC8
## Standard deviation 0.44993
## Proportion of Variance 0.00091
## Cumulative Proportion 1.00000Le due funzioni ritornano risultati molto simili. prcomp() è numericamente più
accurata, ma in qualche modo più lenta per dataset grandi. Nel seguito di questi esempi
proseguiremo quindi usando solo princomp().
Dall’output delle procedure, possiamo vedere che le prime tre PC spiegano più del 97% della variabilità globale, con coefficienti:
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 13.5934012 4.5370290 2.4515180 1.191561472 0.764224458
## Proportion of Variance 0.8620605 0.0960339 0.0280383 0.006623909 0.002724729
## Cumulative Proportion 0.8620605 0.9580944 0.9861327 0.992756588 0.995481317
## Comp.6 Comp.7 Comp.8
## Standard deviation 0.648841377 0.593016147 0.4426119310
## Proportion of Variance 0.001964077 0.001640645 0.0009139611
## Cumulative Proportion 0.997445394 0.999086039 1.0000000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## m0 0.562 0.285 0.287 0.225 0.110 0.494 0.432 0.166
## m25 0.312 -0.336 0.434 -0.414 0.301 -0.533 -0.225
## m50 0.177 -0.433 0.470 0.114 0.222 -0.627 0.316
## m75 -0.334 0.796 -0.364 0.119 -0.323
## w0 0.623 0.387 -0.279 -0.456 -0.306 -0.273
## w25 0.343 -0.268 -0.302 -0.278 -0.351 0.717
## w50 0.197 -0.367 -0.299 -0.168 -0.379 0.478 -0.572
## w75 -0.388 -0.499 0.143 0.729 0.195## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 13.5934012 4.5370290 2.4515180 1.191561472 0.764224458
## Proportion of Variance 0.8620605 0.0960339 0.0280383 0.006623909 0.002724729
## Cumulative Proportion 0.8620605 0.9580944 0.9861327 0.992756588 0.995481317
## Comp.6 Comp.7 Comp.8
## Standard deviation 0.648841377 0.593016147 0.4426119310
## Proportion of Variance 0.001964077 0.001640645 0.0009139611
## Cumulative Proportion 0.997445394 0.999086039 1.0000000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## m0 0.562 0.494 0.432
## m25 0.312 -0.336 0.434 -0.414 0.301 -0.533
## m50 -0.433 0.470 -0.627 0.316
## m75 -0.334 0.796 -0.364 -0.323
## w0 0.623 0.387 -0.456 -0.306
## w25 0.343 -0.302 -0.351 0.717
## w50 -0.367 -0.379 0.478 -0.572
## w75 -0.388 -0.499 0.729I loading sono i coefficienti applicati alle variabili originarie per determinare le componenti principali.
Il parametro cutoff del metodo print() permette di “nascondere” i loading con
valore assoluto inferiore alla soglia specificata. Questo permette
di evidenziare i loading più “rilevanti” nella determinazione delle componenti pricipali.
I loading mostrati sopra, quindi, possono aiutare a dare un nome alle componenti principali.
La prima PC sembra essere dominata (negativamente) dal livello globale di vita attesa: la corrispondente PC sarà tanto più
(negativmente) grande quanto più saranno grandi i valori delle età medie.
La seconda PC, invece, sembra opporre la vita attesa alla nascita con la vita attesa nelle età più avanzate;
cioè, valori maggiori nella seconda PC verranno assegnati a regioni in cui la differenza tra la vita attesa alla
nascita e vita attesa nelle età più avanzate è maggiore.
La terza PC sembra opporre la vita attesa degli uomini con quella delle donne.
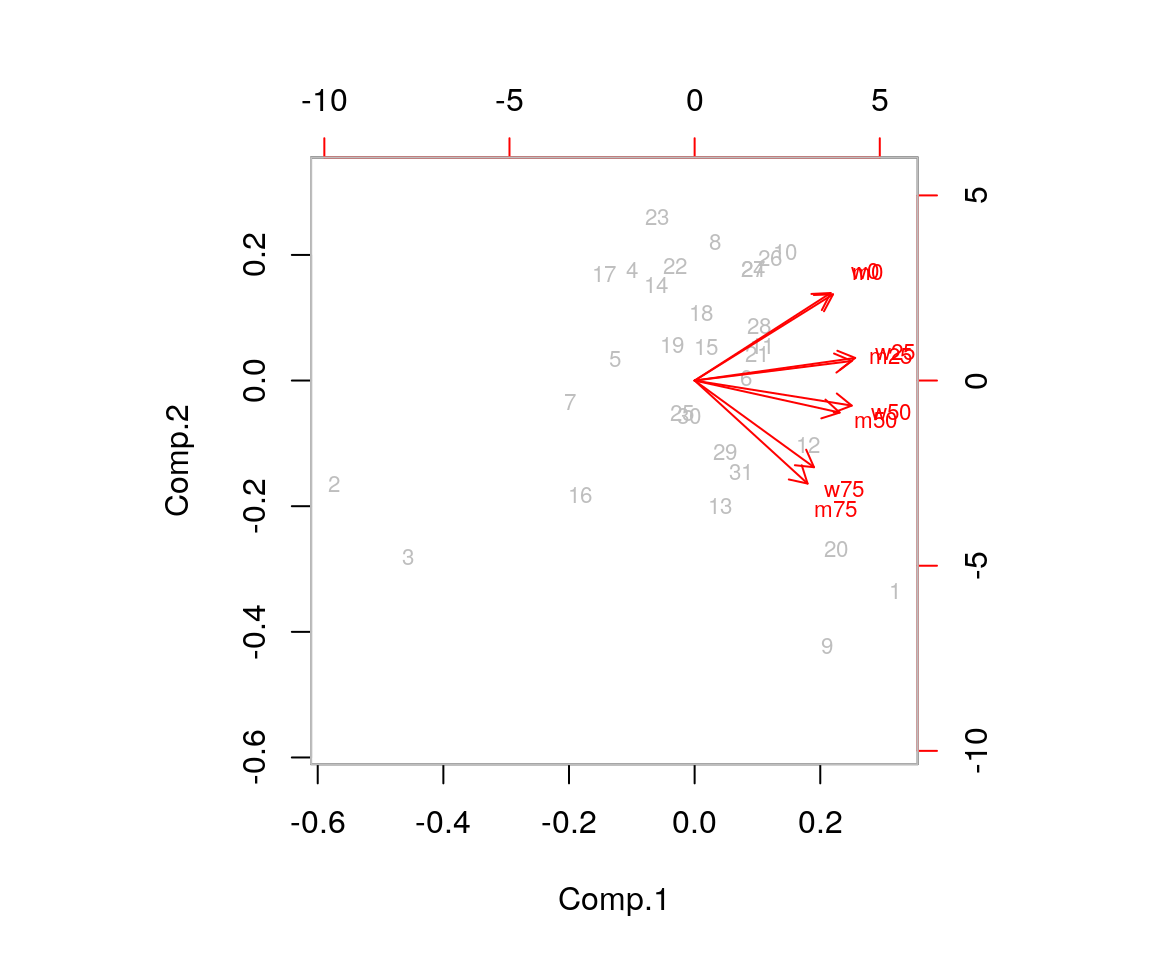
Anche una rappresentazione grafica dei valori di PCA tramite lo scatterplot dei loading può aiutare a “dare un nome” alle PC.
Come già visto, i loading sono parte dell’output prodotto da princomp().
Questo grafico quindi permette al ricercatore di trovare eventuali relazioni tra le componenti principali.
library(ggplot2)
dl <- pca_princomp$loadings
class(dl) <- "matrix"
dl <- data.frame(dl)
dl$gender <- rep(c("maschio", "femmina"), each=4)
dl$age <- rep(as.character((0:3)*25), 2)
ggp <- ggplot(dl, mapping = aes(x=Comp.1, y=Comp.2, colour=gender, shape=age)) +
geom_point() +
scale_shape_manual(values = rep(0:3,2)) +
ggtitle("PC1 Vs PC2 per sesso e età")
print(ggp)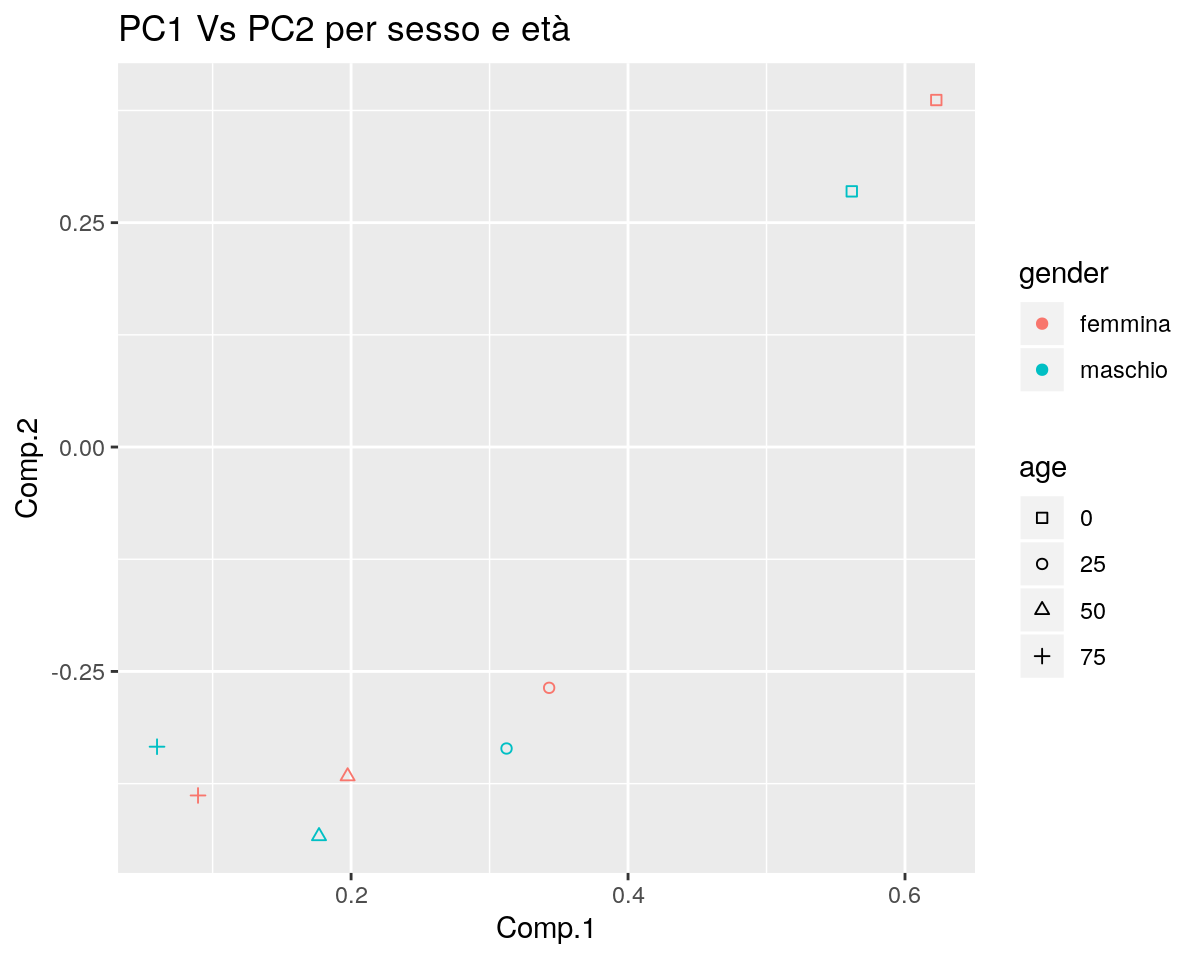
ggp <- ggplot(dl, mapping = aes(x=Comp.1, y=Comp.3, colour=gender, shape=age)) +
geom_point() +
scale_shape_manual(values = rep(0:3,2)) +
ggtitle("PC1 Vs PC3 per sesso e età")
print(ggp)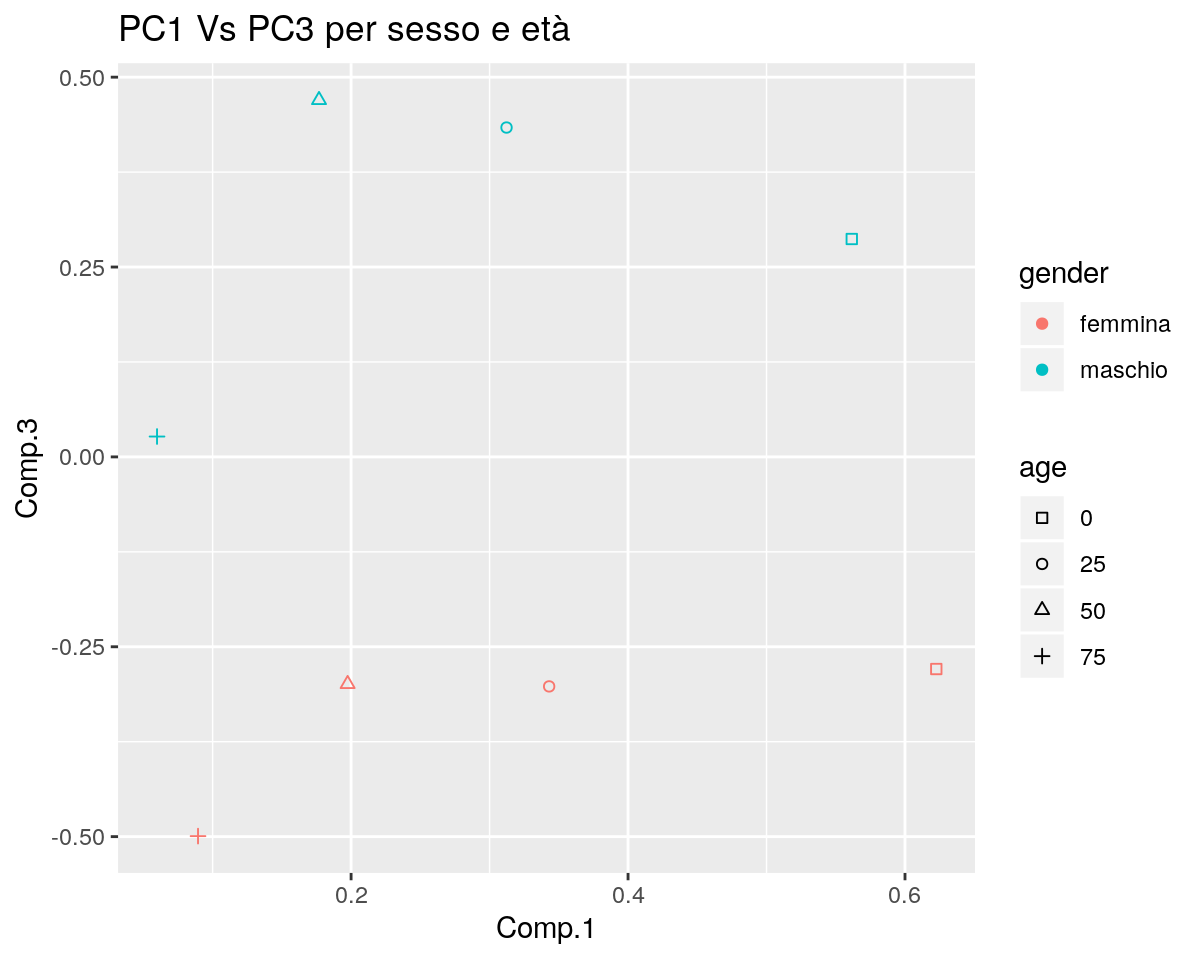
ggp <- ggplot(dl, mapping = aes(x=Comp.2, y=Comp.3, colour=gender, shape=age)) +
geom_point() +
scale_shape_manual(values = rep(0:3,2)) +
ggtitle("PC2 Vs PC3 per sesso e età")
print(ggp)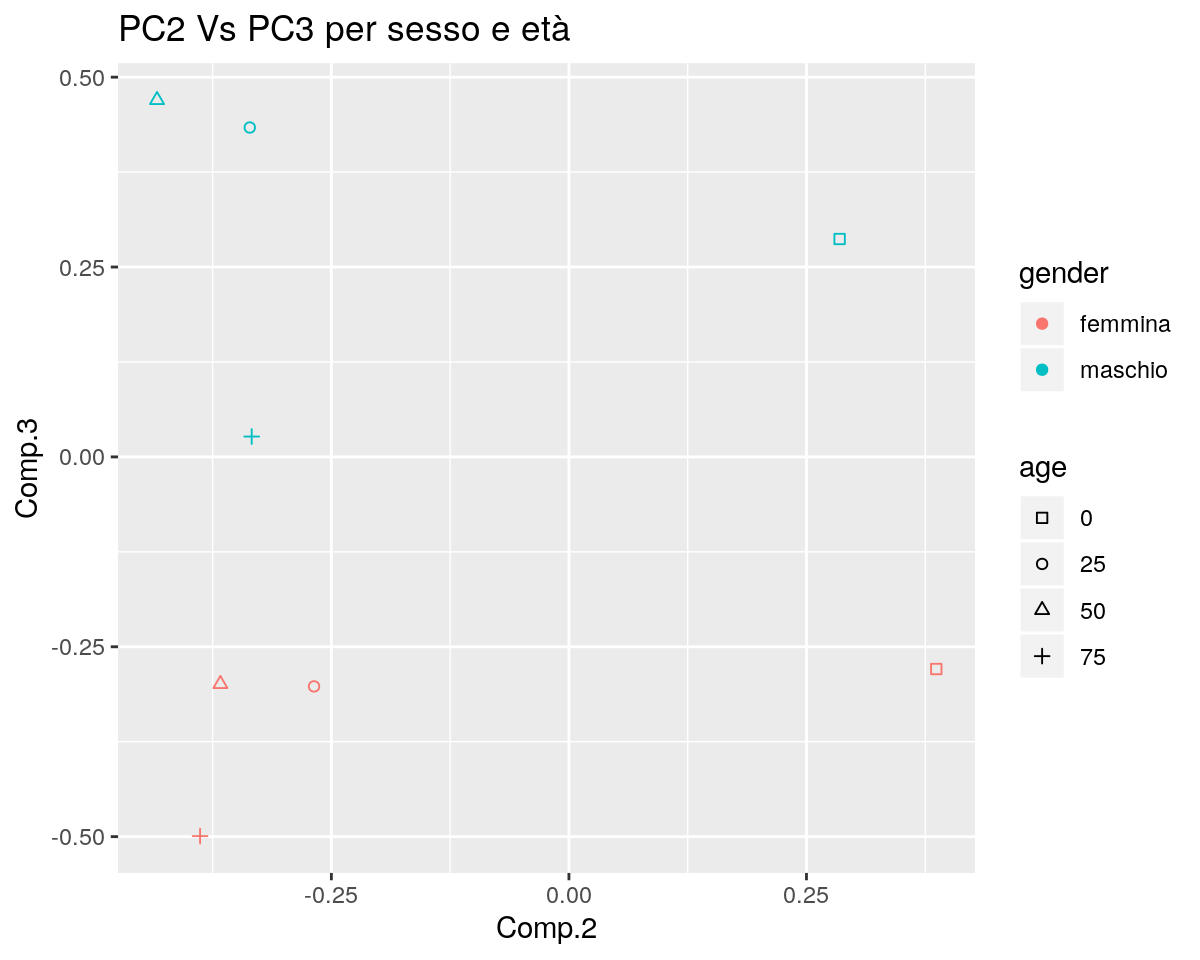
Ora approfondiremo questi risultati analizzando i cosiddetti score o punteggi.
Gli score sono le coordinate dei punti (righe) originali, proiettate sulle componenti principali. Questi rappresentano
le nuove variabili (derivate) che uno può usare in altre analisi, quali per esempio la regressione.
Gli score sono parte dell’output fornito da princomp(). Tipicamente li si può rappresentare
graficamente per cercare caratteristiche nei dati quali cluster, outlier, ecc.
Un utile approccio per interpretare le PC stimate è quello di calcolare le correlazioni dei
punteggi delle PC importanti con ciascuna delle variabili originarie:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## m0 0.9798753 0.1659175 0.09029315 0.03435868 0.010833525 0.041144972
## m25 0.9077778 -0.3258982 0.22739054 -0.10544636 0.011758329 0.041757210
## m50 0.7175522 -0.5871008 0.34389726 0.04066645 0.050642952 -0.121351816
## m75 0.4078898 -0.7593118 0.03300976 0.47518338 -0.139449498 0.038614254
## w0 0.9751856 0.2021222 -0.07889142 0.01121110 0.003964288 -0.034115846
## w25 0.9506882 -0.2481401 -0.15103743 -0.06743001 -0.054685222 -0.007668405
## w50 0.8174017 -0.5067414 -0.22319236 -0.06099452 -0.088174810 0.018831360
## w75 0.4793686 -0.6942651 -0.48254311 0.06719398 0.219750449 0.049935930
## Comp.7 Comp.8
## m0 0.032913705 0.009423358
## m25 -0.067592494 -0.021300334
## m50 0.055941848 0.009586812
## m75 -0.096025917 -0.004940247
## w0 -0.020908721 -0.013906251
## w25 -0.005209272 0.064675175
## w50 0.086362574 -0.077100877
## w75 -0.005522558 0.004944782
La tabella mostra che la prima PC è fortemente correlata, anche negativamente, con tutte le variabili:
la vita attesa entro ciascuna regione decade mano a mano che l’età dei soggetti avanza. Questo significa che
le regioni con un valore più basso nello score della prima PC dvrebbero avere una vita attesa più lunga.
La seconda PC invece pone in contrasto la vita attesa alla nascita con la vita attesa nelle età successive,
dando valore positivo alla vita attesa alla nascita; questo può significare che le regioni con un valore più elevato
nello score della seconda PC dovrebbero avere una maggiore differenza nella vita attesa alla nascita rispetto alle
età più avanzate, indicando probabilmente una minore mortalità infantile.
La terza componente sembra oppore le misure di maschi e femmine. Questo potrebbe indicare che le regioni con valori
più elevati nella terza PC dovebbero avere un valore di vita attesa più lunga per le donne che per gli uomini rispetto
alle altre regioni.
Ora produciamo lo scatterplot degli score delle prime due PC:
pca_sc <- data.frame(pca_princomp$scores, country = life[, 1])
ggplot(pca_sc, aes(x = Comp.1, y = Comp.2, color = country)) +
geom_point() +
geom_text(mapping = aes(label = country), vjust=1) +
theme(legend.position = "none") +
ggtitle("Punteggi Comp.1 Vs Comp.2")
ggplot(pca_sc, aes(x = Comp.1, y = Comp.3, color = country)) +
geom_point() +
geom_text(mapping = aes(label = country), vjust=1) +
theme(legend.position = "none") +
ggtitle("Punteggi Comp.1 Vs Comp.3")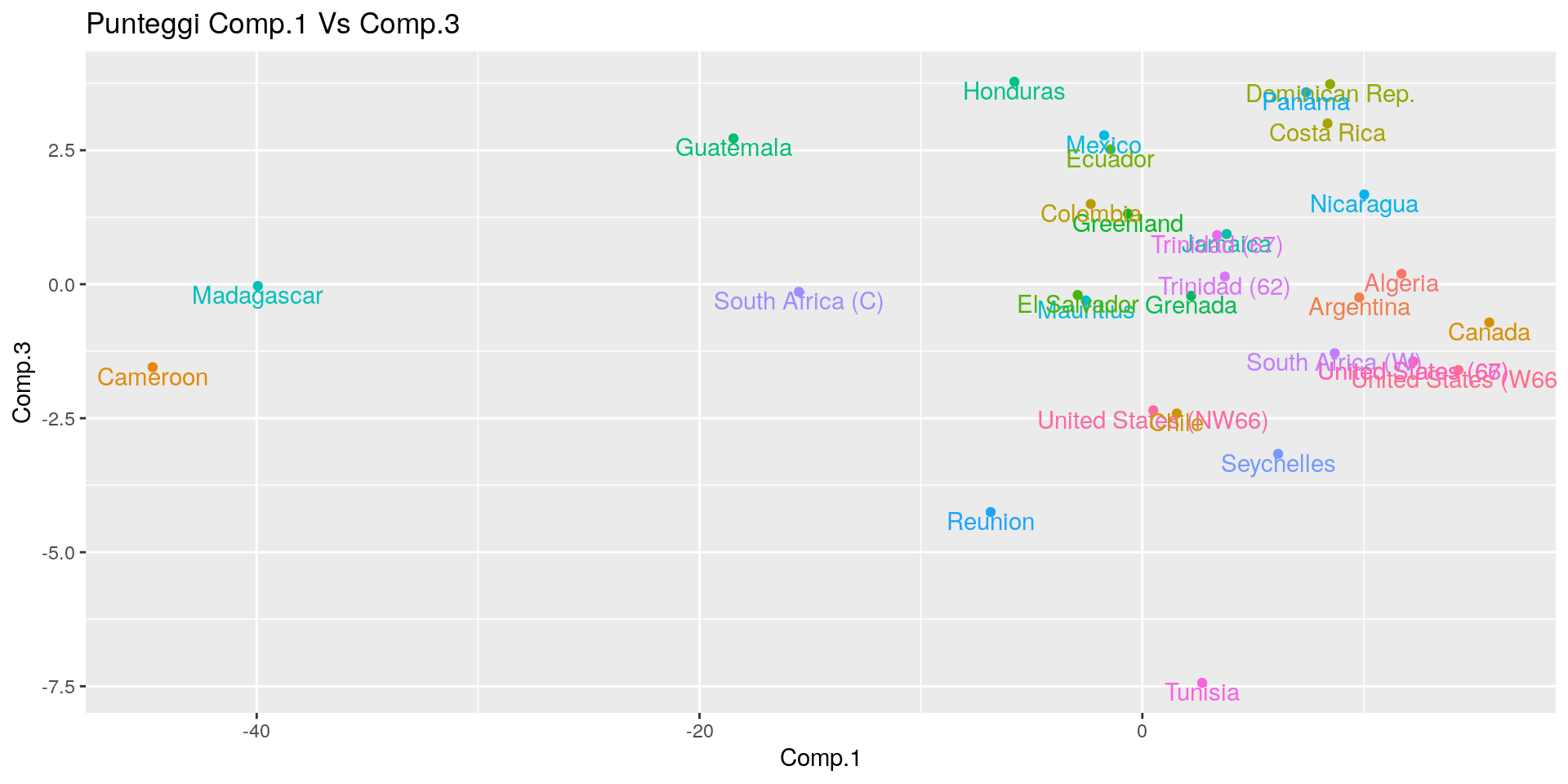
ggplot(pca_sc, aes(x = Comp.2, y = Comp.3, color = country)) +
geom_point() +
geom_text(mapping = aes(label = country), vjust=1) +
theme(legend.position = "none") +
ggtitle("Punteggi Comp.2 Vs Comp.3")
Data l’interpretazione precedentemente fatta delle componenti principali,
la posizione delle diverse aree geografiche nei grafici qui sopra ne identifica
le caratteristiche.
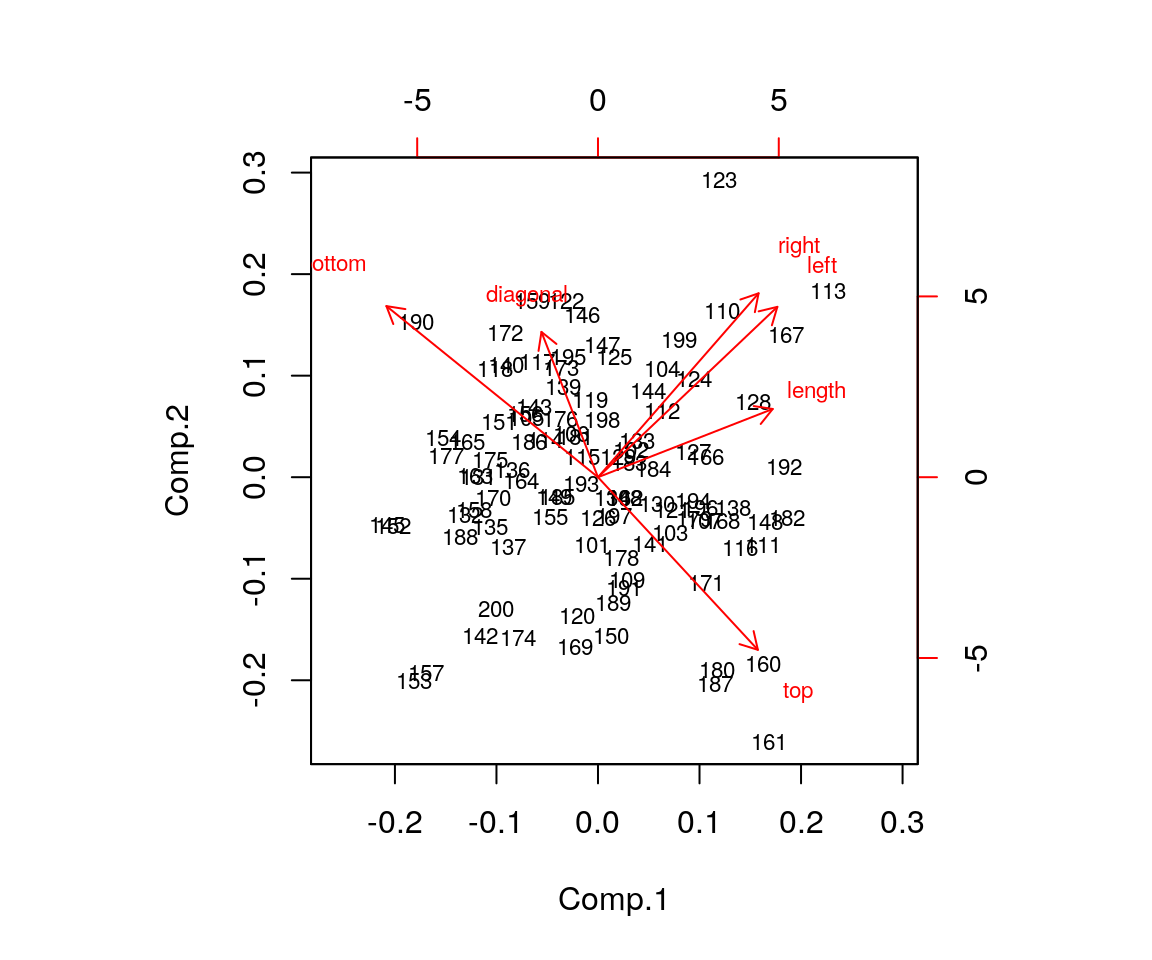
Un’altra rappresentazione grafica dei risultati di una PCA in cui sono rappresentati
sia gli score sia i loading è il biplot, che può essere ottenuta con la funzione biplot():


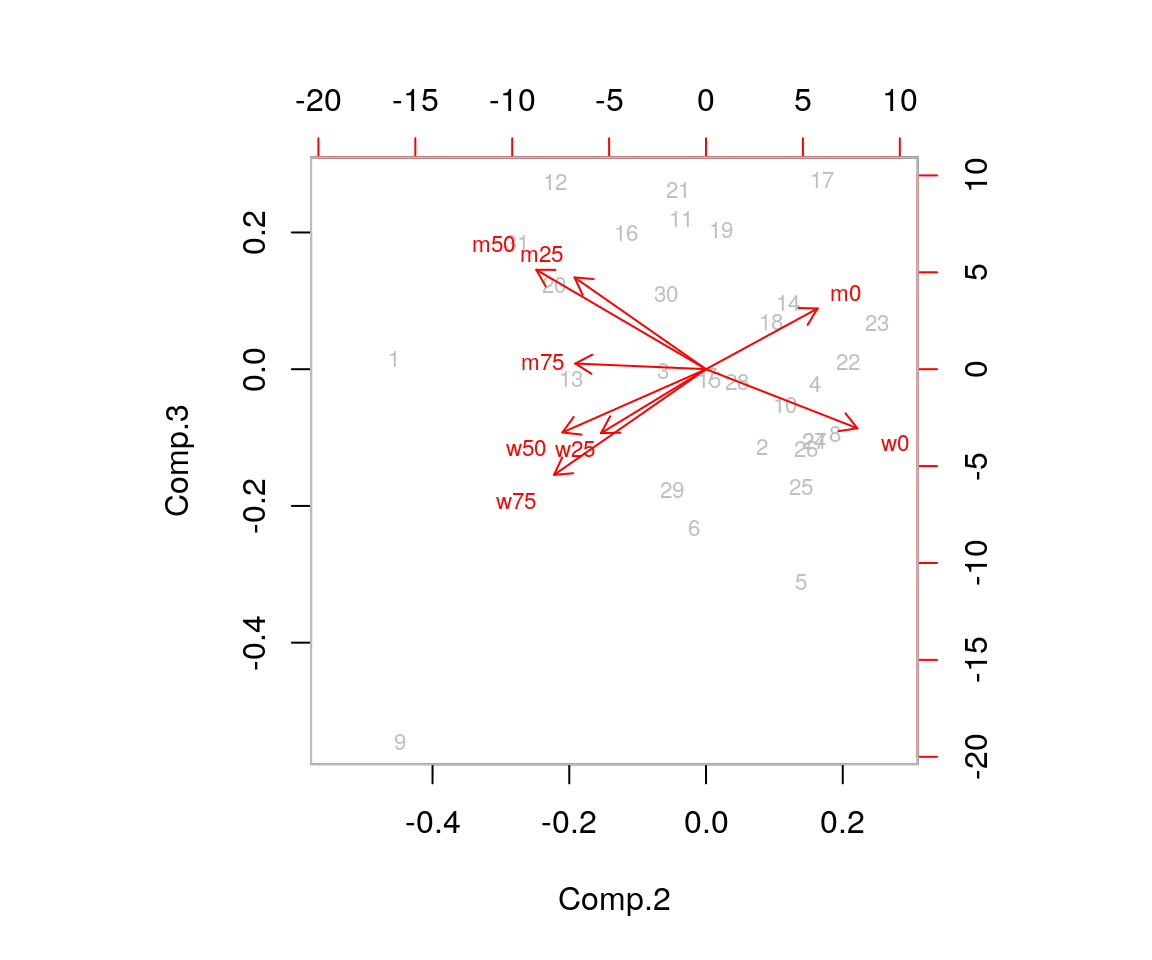
Ora, abbiamo visto che le componenti principali sono trasformazioni lineari delle variabili originarie. Il numero massimo di componenti principali che possono essere estratte da un dataset è uguale al minimo tra il numero di righe ed il numero di colonne del dataset.
Quante PC dovremmo tenere? Questo è probabilmente il problema principale quando si esegue una PCA. Poiché il criterio per una buona proiezione nella PCA è una elevata varianza per quella proiezione, dovremmo tenere solo quelle componenti principali con varianze elevate. Il problema, pertento, coinvolge i valori degli autovalori della matrice di varianza/covarianza (o correlazione) campionaria. Diversi criteri sono stati introdoti in letteratura, e qui di seguito ne vediamo i più popolari:
- varianza spiegata: si tiene un numero di componenti sufficiente a riprodurre una grande percentuale pre-specificata della variabilità complessiva delle variabili originarie. Sono usualmente suggeriti valori compresi tra il 70% e il 90%.
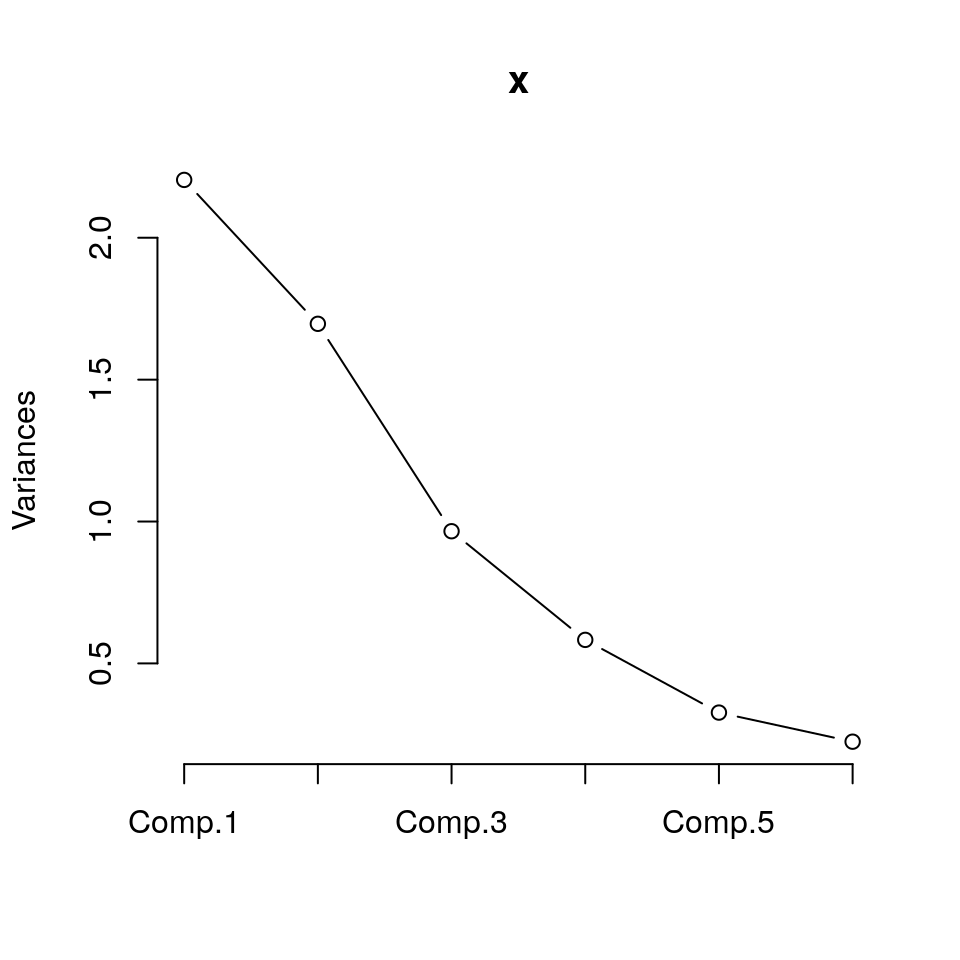
- scree plot: questo è un grafico che rappresenta gli aoutovalori ordinati in senso decescente (asse y) verso il loro numero d’ordine (assex). Se i più grandi autovalori campionari dominano in dimensione, ed i rimanenti autovalori campionari sono molto piccoli, allora lo scree plot mostrerà un “gomito” nel grafico in corrispondenza alla divisione tra “grandi” e “piccoli” valori degli autovalori campionari. La posizione in cui si presenta il gomito, può essere usata come numero di PC da tenere.
- Regola di Kaiser: tenere solo le PC i cui autovalori superano il valore 1.
Questa linea guida si basa sull’idea che, poichè la variabilità
totale di tutte le \(p\) variabili standardizzate è uguale a
p, ne segue che una PCA dovrebbe spiegare almeno una variazione pari al valore medio di una singola variabile standardizzata. Questa regola è popolare ma controversa; c’è evidenza che il valore limite di 1 è generalmente troppo alto. Una regola modificata dice di tenere tutte le PC i cui autovalori della correlazione campionaria superano 0.7. Ovviamente, per dati non standardizzati, questa regola non ha senso applicarla.
Per il nostro esempio dei dati di vita attesa, il criterio della varianza spiegata suggerirebbe di non usare più di 2 componenti. Lo scree plot, dato da
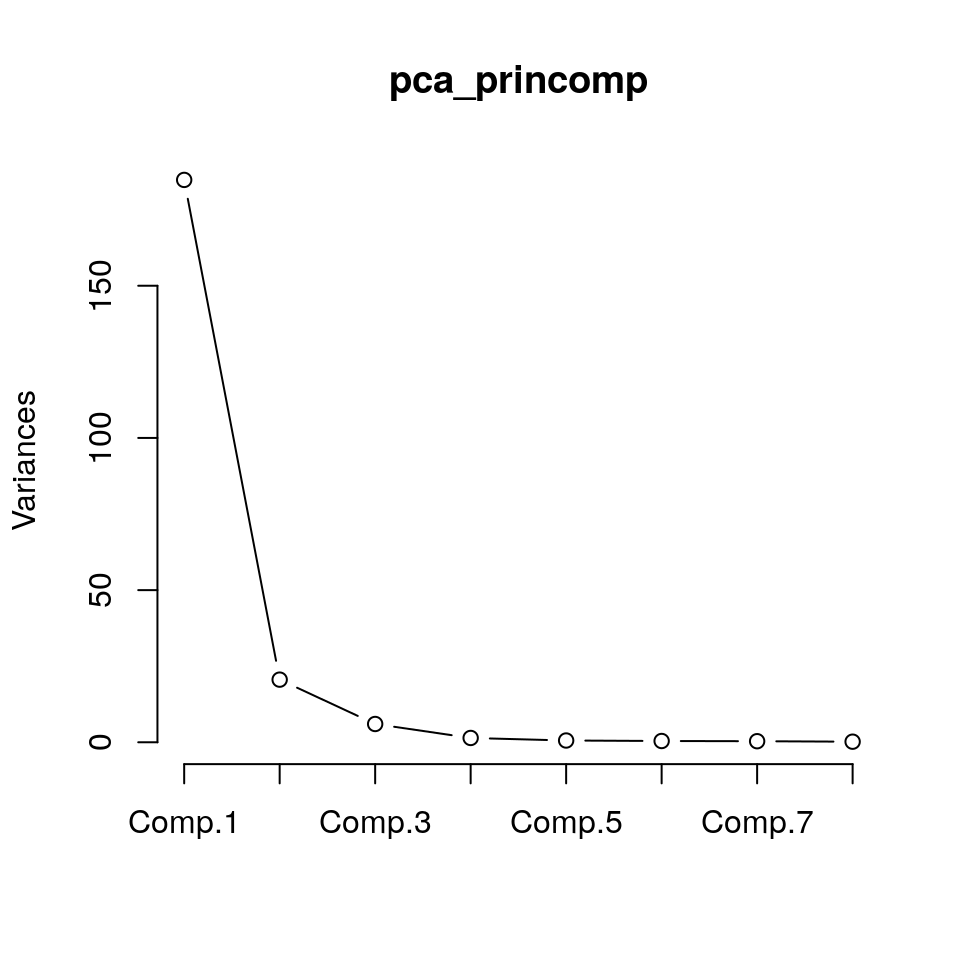
suggerirebbe due o al più tre componenti (si noti che le varianze riportate sull’asse verticale di questo grafico corrispondono agli autoavalori della matrice di varianze/covarianze dei dati originali). La regola di Kaiser suggerisce 4 componenti, probabilmente un valore un po’ alto, se l’obiettivo è ottenere un sunto dell’informazione complessiva contenuta nei dati originali.
Un grafico tridimensionale delle prime tre PC può essere prodotto con la funzione
plot3d() del package rgl (il grafico può essere fatto ruotare col ):
plot3d(pca_princomp$scores[, 1:3], size = 5)
texts3d(pca_princomp$scores[, 1:3], texts = life$country, adj = c(0.5,0))
play3d(spin3d(axis = c(1, 1, 1), rpm = 15), duration = 10)(Nota: il comando qui sopra mostra un grafico 3D dinamico che non può ovviamente essere mostrato qui)
4.2.2 Esempio: Correlazioni sui dati di vita attesa
In questo prosieguo di esempio, sono eseguite le stesse elaborazioni dell’esempio precedente, con i dati però standardizzati
prima di applicare la PCA. Ciò rende i valori delle diverse variabili più confrontabili e con “peso”
uguale durante la PCA, perché la varianza delle variabili è costante.
Le opzioni cor = TRUE e center = TRUE, scale. = TRUE permettono a princomp() e prcomp()
(rispettivamente) di calcolare le PCA sulle variabili standardizzate.
## user system elapsed
## 0.002 0.001 0.001## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 2.4311566 1.1466229 0.69791483 0.42937156 0.244503441
## Proportion of Variance 0.7388153 0.1643430 0.06088564 0.02304499 0.007472742
## Cumulative Proportion 0.7388153 0.9031583 0.96404394 0.98708893 0.994561674
## Comp.6 Comp.7 Comp.8
## Standard deviation 0.158855457 0.113103100 0.0740218822
## Proportion of Variance 0.003154382 0.001599039 0.0006849049
## Cumulative Proportion 0.997716056 0.999315095 1.0000000000## user system elapsed
## 0.001 0.000 0.001## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 2.4312 1.1466 0.69791 0.42937 0.24450 0.15886 0.1131
## Proportion of Variance 0.7388 0.1643 0.06089 0.02304 0.00747 0.00315 0.0016
## Cumulative Proportion 0.7388 0.9032 0.96404 0.98709 0.99456 0.99772 0.9993
## PC8
## Standard deviation 0.07402
## Proportion of Variance 0.00068
## Cumulative Proportion 1.00000Le due funzioni ritornano risultati molto simili. Nel resto di questo esempio
si proseguirà usando la funzione princomp().
Dall’output possiamo vedere che le prime tre PC spiegano più del 96% della variabilità totale, con i seguenti coefficienti:
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 2.4311566 1.1466229 0.69791483 0.42937156 0.244503441
## Proportion of Variance 0.7388153 0.1643430 0.06088564 0.02304499 0.007472742
## Cumulative Proportion 0.7388153 0.9031583 0.96404394 0.98708893 0.994561674
## Comp.6 Comp.7 Comp.8
## Standard deviation 0.158855457 0.113103100 0.0740218822
## Proportion of Variance 0.003154382 0.001599039 0.0006849049
## Cumulative Proportion 0.997716056 0.999315095 1.0000000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## m0 0.345 0.456 0.267 0.246 0.424 0.596
## m25 0.392 0.104 0.297 -0.335 -0.766 0.108 -0.191
## m50 0.362 -0.169 0.552 -0.399 0.263 0.542 -0.114
## m75 0.282 -0.545 0.312 0.709 -0.115
## w0 0.339 0.463 -0.172 0.319 0.170 0.182 -0.118 -0.680
## w25 0.400 0.120 -0.207 -0.283 -0.752 0.366
## w50 0.392 -0.132 -0.260 -0.179 -0.670 0.247 0.460
## w75 0.298 -0.458 -0.605 -0.140 0.551## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 2.4311566 1.1466229 0.69791483 0.42937156 0.244503441
## Proportion of Variance 0.7388153 0.1643430 0.06088564 0.02304499 0.007472742
## Cumulative Proportion 0.7388153 0.9031583 0.96404394 0.98708893 0.994561674
## Comp.6 Comp.7 Comp.8
## Standard deviation 0.158855457 0.113103100 0.0740218822
## Proportion of Variance 0.003154382 0.001599039 0.0006849049
## Cumulative Proportion 0.997716056 0.999315095 1.0000000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## m0 0.345 0.456 0.424 0.596
## m25 0.392 -0.335 -0.766
## m50 0.362 0.552 -0.399 0.542
## m75 -0.545 0.312 0.709
## w0 0.339 0.463 0.319 -0.680
## w25 0.400 -0.752 0.366
## w50 0.392 -0.670 0.460
## w75 -0.458 -0.605 0.551Anche in questo caso la prima PC sembra dominata (negativamente) dal livello globale del valore di vita attesa.
La seconda PC sembra contrapporre la vita attesa nelle età giovanili con la vita
attesa nelle età più avanzate.
La terza PC ontrappone la vita attesa degli uomini e delle donne.
La rappresentazione grafica dell’analisi di PCA tramite scatterplot dei loading può ancora aiutare nel dare nome alle Pc.
library(ggplot2)
dl <- pca_princomp$loadings
class(dl) <- "matrix"
dl <- data.frame(dl)
dl$gender <- rep(c("maschio", "femmina"), each=4)
dl$age <- rep(as.character((0:3)*25), 2)
ggp <- ggplot(dl, mapping = aes(x=Comp.1, y=Comp.2, colour=gender, shape=age)) +
geom_point() +
scale_shape_manual(values = rep(0:3,2)) +
ggtitle("PC1 Vs PC2 per sesso e età")
print(ggp)
ggp <- ggplot(dl, mapping = aes(x=Comp.1, y=Comp.3, colour=gender, shape=age)) +
geom_point() +
scale_shape_manual(values = rep(0:3,2)) +
ggtitle("PC1 Vs PC3 per sesso e età")
print(ggp)
ggp <- ggplot(dl, mapping = aes(x=Comp.2, y=Comp.3, colour=gender, shape=age)) +
geom_point() +
scale_shape_manual(values = rep(0:3,2)) +
ggtitle("PC2 Vs PC3 per sesso e età")
print(ggp)
Ora pprofondiamo qusti risultati con l’analisi degli score.
Cominciamo dal calcolo delle correlazioni degli score delle PC con tutte le variabili originali:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## m0 0.8390946 0.5227327 0.03923331 0.11483293 0.0602238305 0.008705220
## m25 0.9524142 0.1186975 0.20736179 -0.14368405 0.0002258456 -0.121757701
## m50 0.8791358 -0.1940125 0.38531740 -0.17112036 0.0643765383 0.086097267
## m75 0.6847714 -0.6245093 0.21786502 0.30451359 -0.0231223093 -0.018326309
## w0 0.8244105 0.5308659 -0.12019789 0.13714125 0.0414456127 0.028986718
## w25 0.9732376 0.1372837 -0.14479074 -0.01446390 -0.0691075198 -0.006762882
## w50 0.9523955 -0.1517311 -0.18142976 -0.07681211 -0.1637531747 0.039234925
## w75 0.7236413 -0.5254190 -0.42223648 -0.06000416 0.1347861331 -0.012664868
## Comp.7 Comp.8
## m0 0.047916929 0.044115946
## m25 0.012235665 -0.014117481
## m50 -0.012859570 -0.002298165
## m75 -0.002879561 -0.001954258
## w0 -0.013368252 -0.050366442
## w25 -0.085034852 0.027124636
## w50 0.051973909 -0.006914984
## w75 0.007872979 0.002068105
La tabella mostra anche in questo caso che la prima PC è legata negativamente con tutte le variabili:
la vita attesa entro ciascuna regione cala al crescere dell’età dei soggetti.
La seconda PC instead contrappone la vita attesa in età giovanile (non più solo alla nascita) con la vita attesa in età più avanzate.
La terza PC anche in questo caso contrappone i maschi e le femmine.
Qui di seguito quindi gli scatterplot degli score delle prime tre PC:
pca_sc <- data.frame(pca_princomp$scores, country = life[, 1])
ggplot(pca_sc, aes(x = Comp.1, y = Comp.2, color = country)) +
geom_point() +
geom_text(mapping = aes(label = country), vjust=1) +
theme(legend.position = "none") +
ggtitle("Score Comp.1 Vs Comp.2")
ggplot(pca_sc, aes(x = Comp.1, y = Comp.3, color = country)) +
geom_point() +
geom_text(mapping = aes(label = country), vjust=1) +
theme(legend.position = "none") +
ggtitle("Score Comp.1 Vs Comp.3")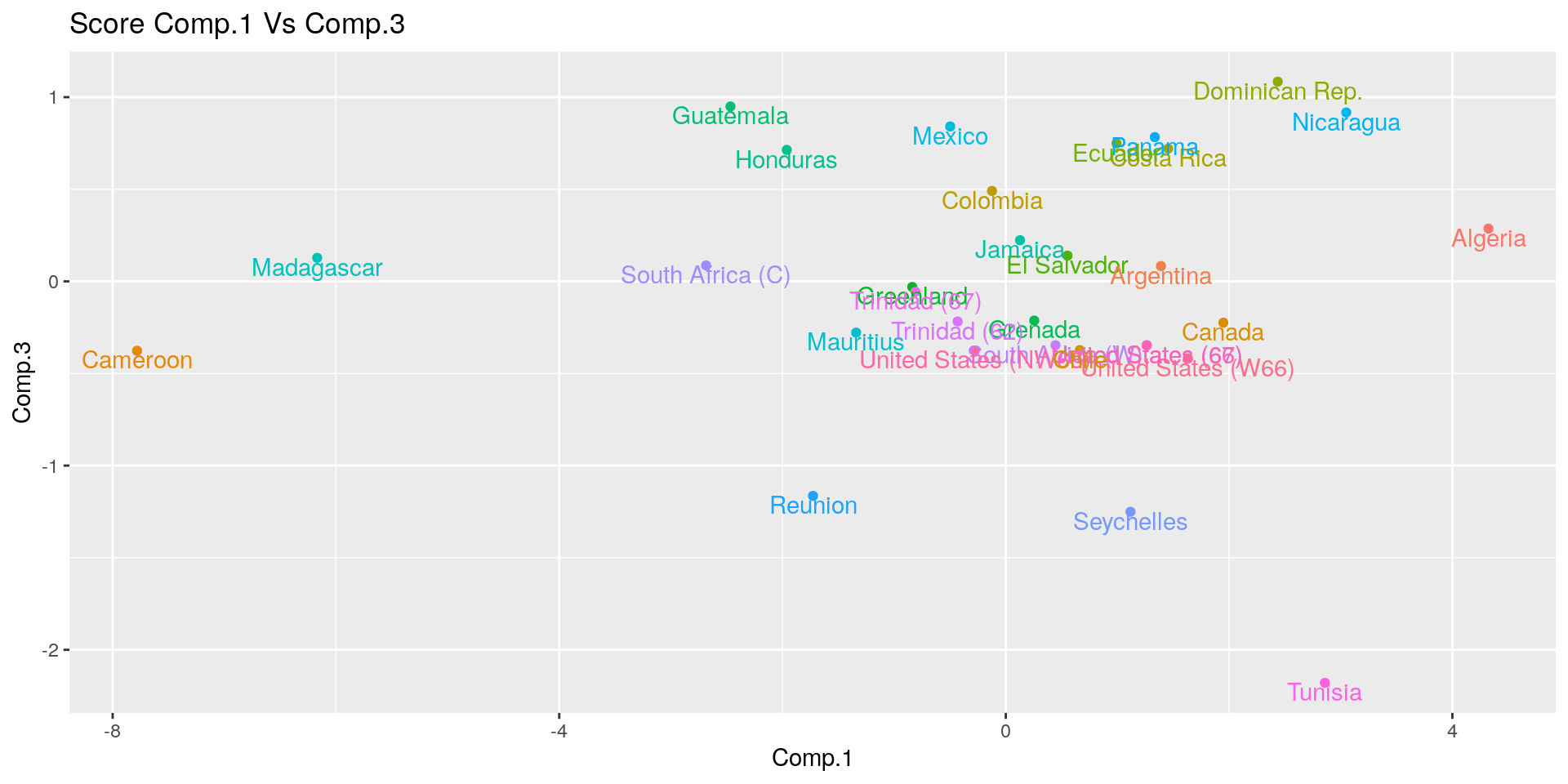
ggplot(pca_sc, aes(x = Comp.2, y = Comp.3, color = country)) +
geom_point() +
geom_text(mapping = aes(label = country), vjust=1) +
theme(legend.position = "none") +
ggtitle("Score Comp.2 Vs Comp.3")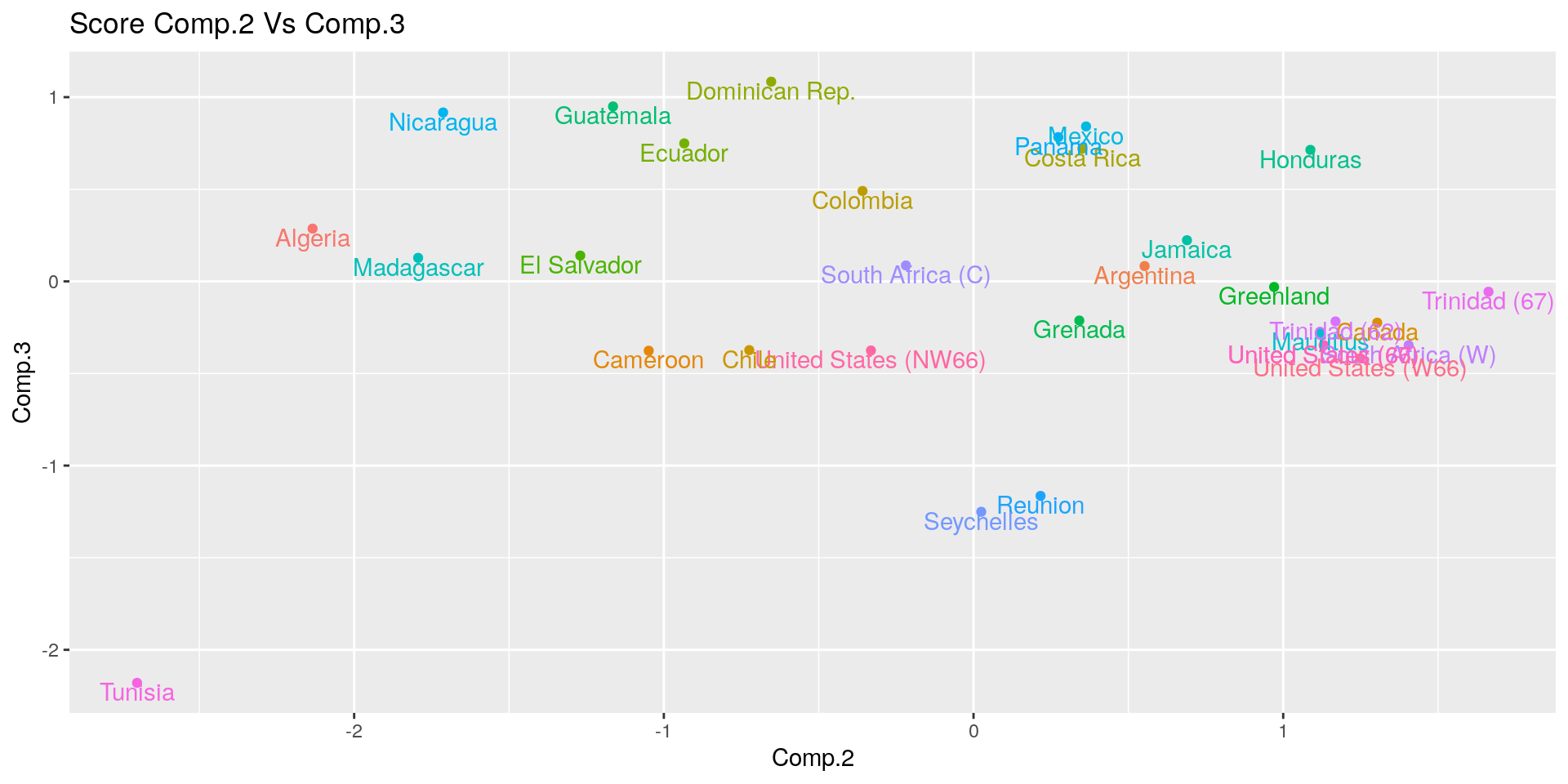
L’ultima rappresentazione grafica dei risultati della PCA è il biplot,
che otteniamo tramite la funzione biplot():


Anche in questo caso, volendo cercare il numero “corretto” di componenti per rappresentare i dati, possiamo produrre lo scree plot:

Questo grafico suggerirebbe due o al più 3 componenti. La regola di Kaiser suggerisce 2 componenti, probabilmente un valore, se l’obiettivo è ottenere un sunto dell’informazione complessiva contenuta nei dati originali.
Infine, il grafico tridimensionale delle prime tre PC può essere ottenuto con la funzione
plot3d() del package rgl (grafico ruotabile con il mouse):
4.2.3 Esempio: Banconote
Consideriamo ora il dataset banknotes. Questo esempio è relativo a sei misure prese su 100 banconote genuine e 100 banconote contraffatte delle vecchie banconote svizzere da 1000 franchi. Le sei misure sono date dalle variabili:
- lunghezza della banconota;
- altezza della banconota, misurata sul bordo sinistro;
- altezza della banconota, misurata sul bordo destro;
- distanza del riquadro interno dak bordo inferiore;
- distanza del riquadro interno dak bordo superiore;
- lunghezza della diagonale.
Le osservazioni (righe) da 1 a 100 sono relative a banconote genuine; le altre 100 osservazioni sono relative a banconote contraffatte.
## Classes 'tbl_df', 'tbl' and 'data.frame': 200 obs. of 7 variables:
## $ length : num 215 215 215 215 215 ...
## $ left : num 131 130 130 130 130 ...
## $ right : num 131 130 130 130 130 ...
## $ bottom : num 9 8.1 8.7 7.5 10.4 9 7.9 7.2 8.2 9.2 ...
## $ top : num 9.7 9.5 9.6 10.4 7.7 10.1 9.6 10.7 11 10 ...
## $ diagonal: num 141 142 142 142 142 ...
## $ type : Factor w/ 2 levels "counterfeit",..: 2 2 2 2 2 2 2 2 2 2 ...## length left right bottom top
## Min. :213.8 Min. :129.0 Min. :129.0 Min. : 7.200 Min. : 7.70
## 1st Qu.:214.6 1st Qu.:129.9 1st Qu.:129.7 1st Qu.: 8.200 1st Qu.:10.10
## Median :214.9 Median :130.2 Median :130.0 Median : 9.100 Median :10.60
## Mean :214.9 Mean :130.1 Mean :130.0 Mean : 9.418 Mean :10.65
## 3rd Qu.:215.1 3rd Qu.:130.4 3rd Qu.:130.2 3rd Qu.:10.600 3rd Qu.:11.20
## Max. :216.3 Max. :131.0 Max. :131.1 Max. :12.700 Max. :12.30
## diagonal type
## Min. :137.8 counterfeit:100
## 1st Qu.:139.5 genuine :100
## Median :140.4
## Mean :140.5
## 3rd Qu.:141.5
## Max. :142.4Useremo solo le prime sei colonne del data frame perché l’ultima (type) contiene informazioni testuali e quindi non può essere usata in una PCA. La useremo però per rappresentare graficamente i risultati.
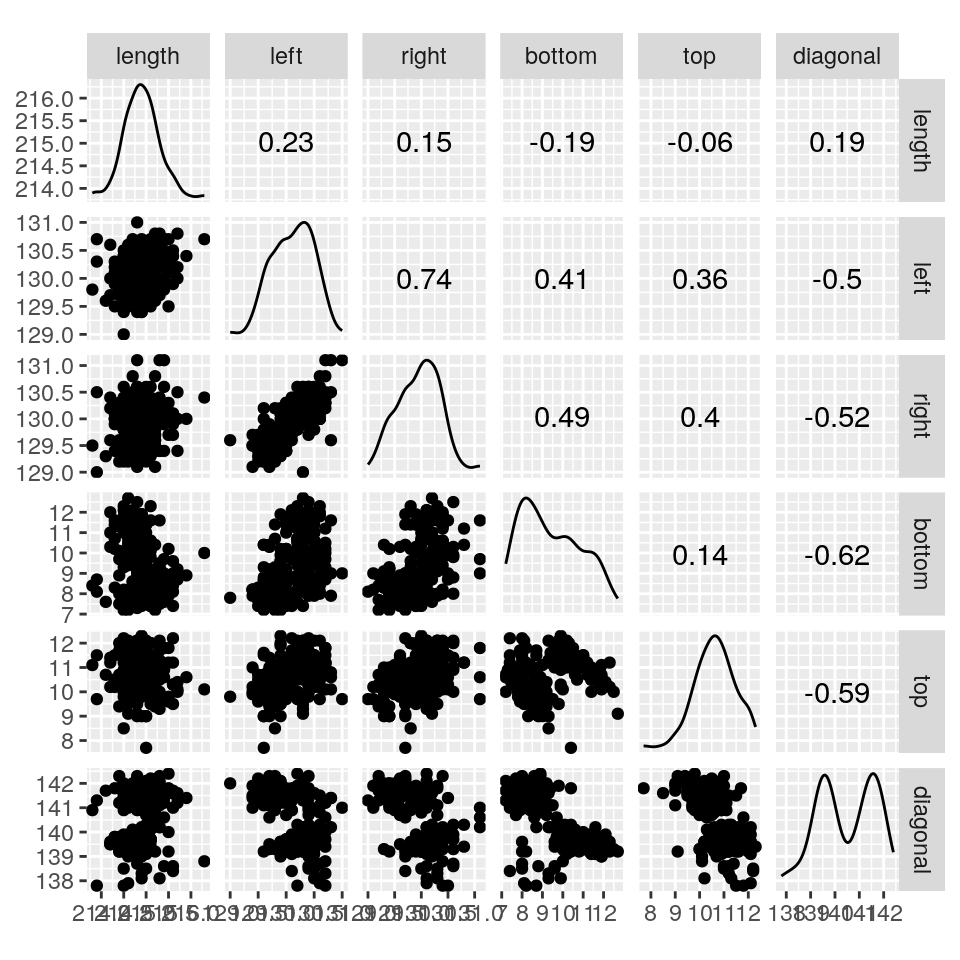

Come si vede dalla matrice di scatterplot, alcune delle variabili originarie sono
correlate; potrebbe quindi avere senso pre-elaborare i dati con la PCA.
Per dare un peso uguale a tutte le variabili, provvederemo prima a standardizzarle.
Possiamo farlo usando l’argomento opzionale cor = TRUE in princomp().
Come già detto, questo corriponde a eseguire una PCA sulla matrice di correlazione
delle variabili originarie:
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.7162629 1.1305237 0.9322192 0.67064796 0.51834053
## Proportion of Variance 0.4909264 0.2130140 0.1448388 0.07496145 0.04477948
## Cumulative Proportion 0.4909264 0.7039403 0.8487791 0.92374054 0.96852002
## Comp.6
## Standard deviation 0.43460313
## Proportion of Variance 0.03147998
## Cumulative Proportion 1.00000000Dall’output possiamo vedere che le prime 3 componenti spiegano più dell’84% della variabilità totale, e hanno coefficienti:
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.7162629 1.1305237 0.9322192 0.67064796 0.51834053
## Proportion of Variance 0.4909264 0.2130140 0.1448388 0.07496145 0.04477948
## Cumulative Proportion 0.4909264 0.7039403 0.8487791 0.92374054 0.96852002
## Comp.6
## Standard deviation 0.43460313
## Proportion of Variance 0.03147998
## Cumulative Proportion 1.00000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## length 0.815 0.575
## left -0.468 0.342 -0.103 -0.395 -0.639 -0.298
## right -0.487 0.252 -0.123 -0.430 0.614 0.349
## bottom -0.407 -0.266 -0.584 0.404 0.215 -0.462
## top -0.368 0.788 0.110 0.220 -0.419
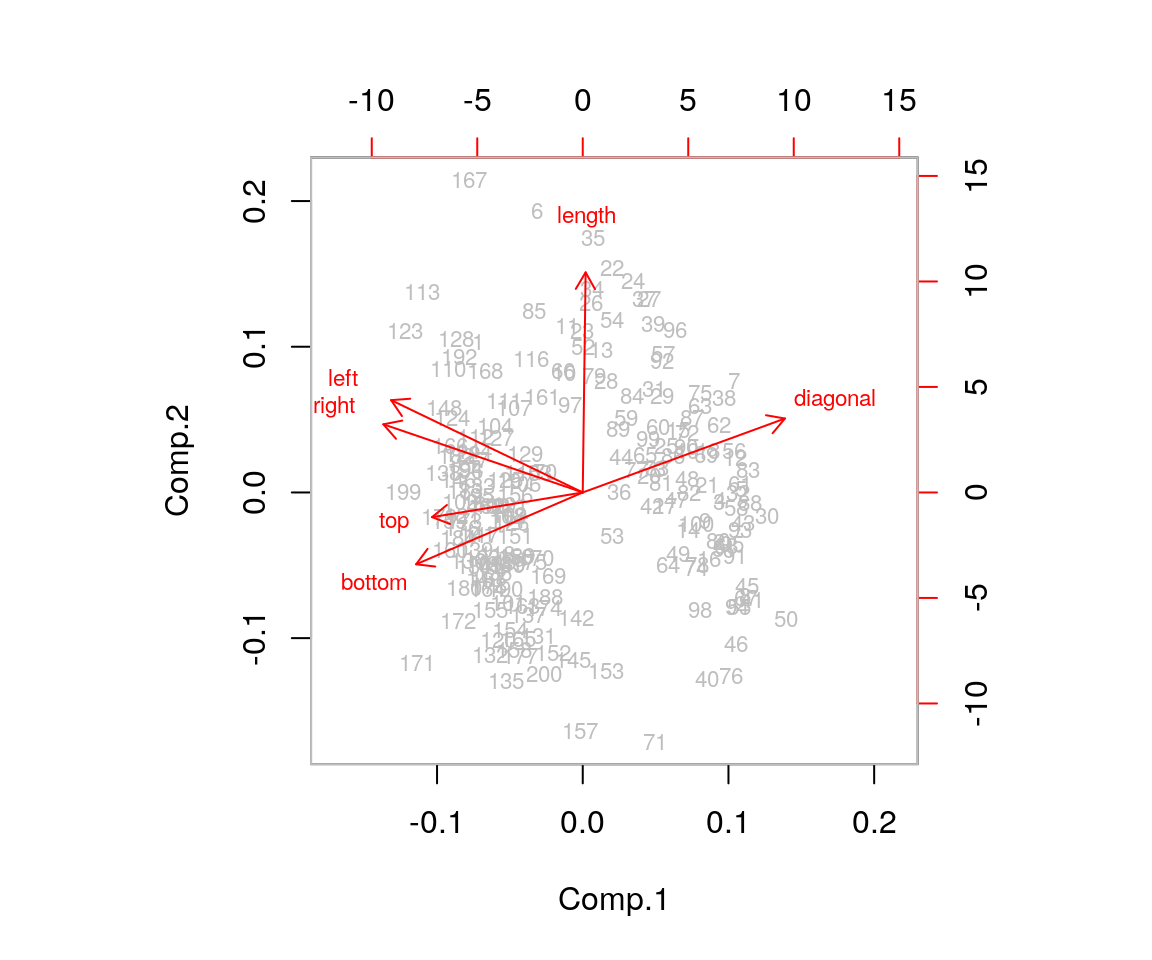
## diagonal 0.493 0.274 -0.114 -0.392 0.340 -0.632Ora usiamo le correlazioni degli score delle PC con ciascuna delle variabili originali per interpretare le componenti:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## length 0.01199158 0.9219364 0.01648225 0.38536590 0.0304764 0.01349746
## left -0.80279596 0.3866019 -0.09637548 -0.26485400 -0.3314768 -0.12940207
## right -0.83526859 0.2854104 -0.11510550 -0.28856524 0.3183114 0.15174296
## bottom -0.69810421 -0.3009779 -0.54398559 0.27072283 0.1116898 -0.20094033
## top -0.63139786 -0.1034278 0.73418921 0.07392333 0.1139569 -0.18208461
## diagonal 0.84690418 0.3096965 -0.10615680 -0.26284740 0.1763188 -0.27458160
La tabella mostra che la prima PC fortemete correlata con l’altezza misurata a destra e sinistra, ed è inversamente correlata con la lunghezza della diagonale. La seconda PC rappresenta invece la lunghezza della banconota. La terza componente contrappone le distanze del riquadro inferiore con i bordi inferiore e superiore, mentre le rimanenti PC non sembrano essere correlate in maniera evidente ad alcuna delle variabili originarie.
Tracciamo quindi uno scatterplot delle prime due PC:
pca_sc <- data.frame(pca_princomp$scores, type = banknotes[, 7])
ggplot(pca_sc, aes(x = Comp.1, y = Comp.2, color = type)) +
geom_point()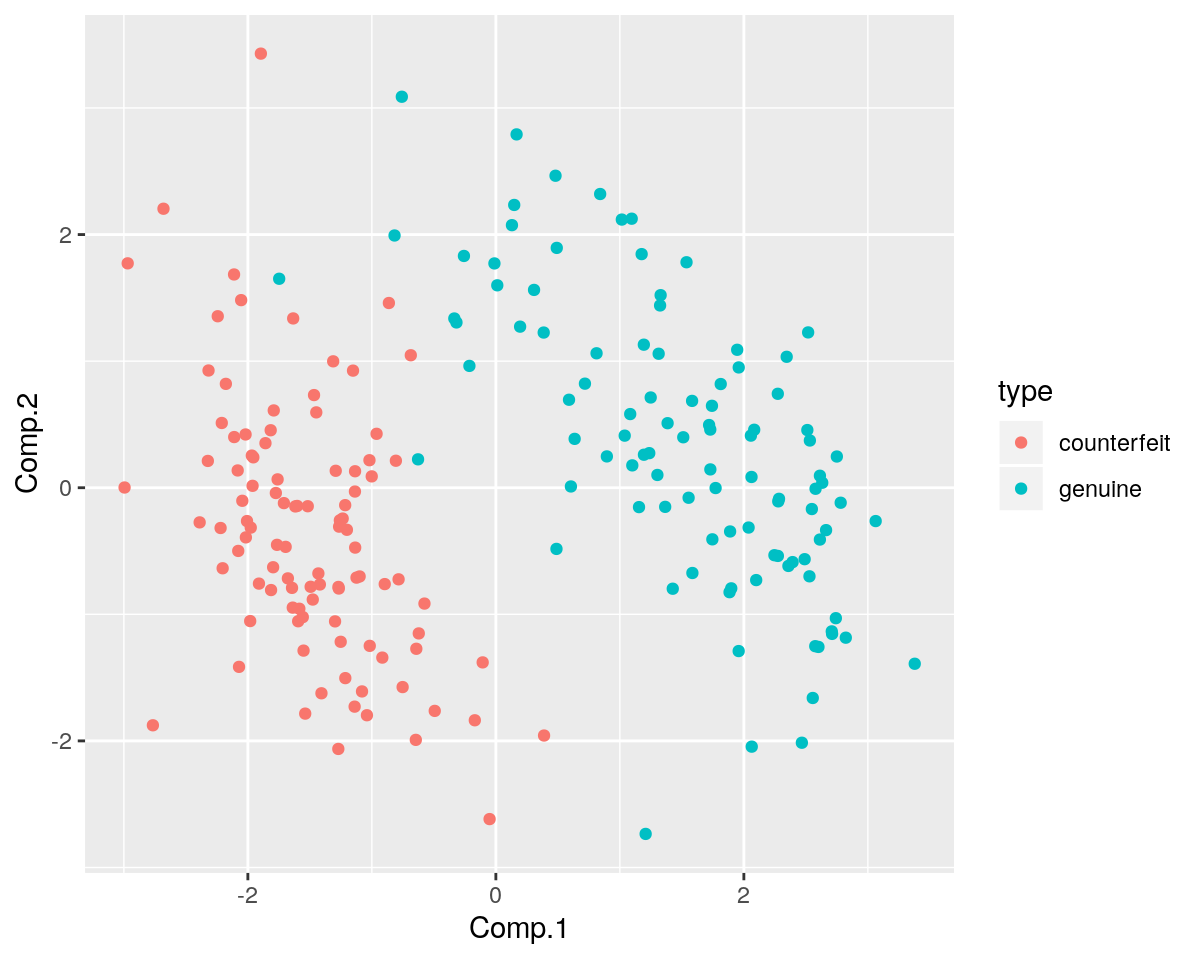
Lo scatterplot mostra che le prime due componenti (anche se questo non è l’obiettivo finale di questa analisi)
permettono di separare quasi perfettamente i due gruppi di banconote (genuine e contraffatte) e qusto potrebbe
quindi anche facilitare la classificazione delle banconote nei due gruppi.
Ora proviamo a usare la funzione biplot():
Ora, quante componenti potremmo voler tenere? La varianza spiegata suggerirebbe di usare 3 componenti. Lo scree plot, dato da
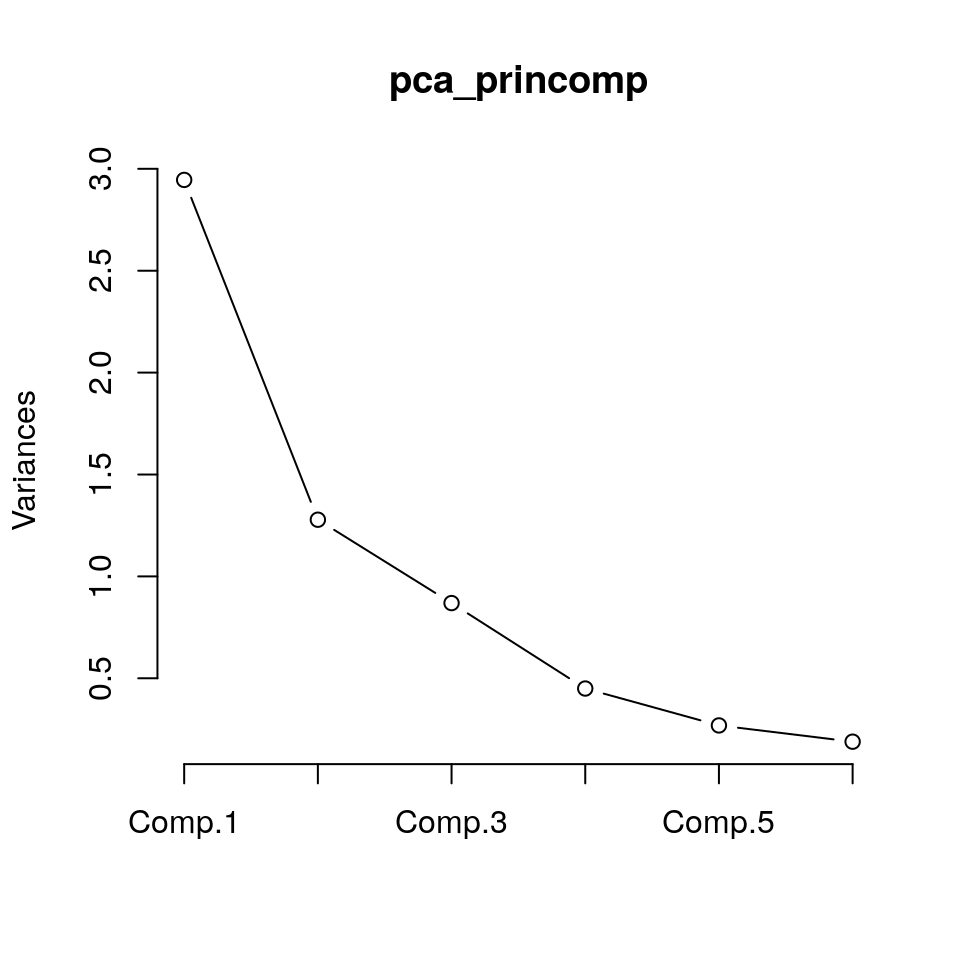
non fornisce suggerimenti utili sul numero di PC perché non si vede un chiaro “gomito” nel grafico. La regola di Kaiser suggerirebbe di usare 3 componenti per avere un buon sunto dell’informazione complessiva contenuta nei dati originari.
Per tracciare gli score per componenti diversi dalle prime due, possiamo usare comunque
la funzione biplot():
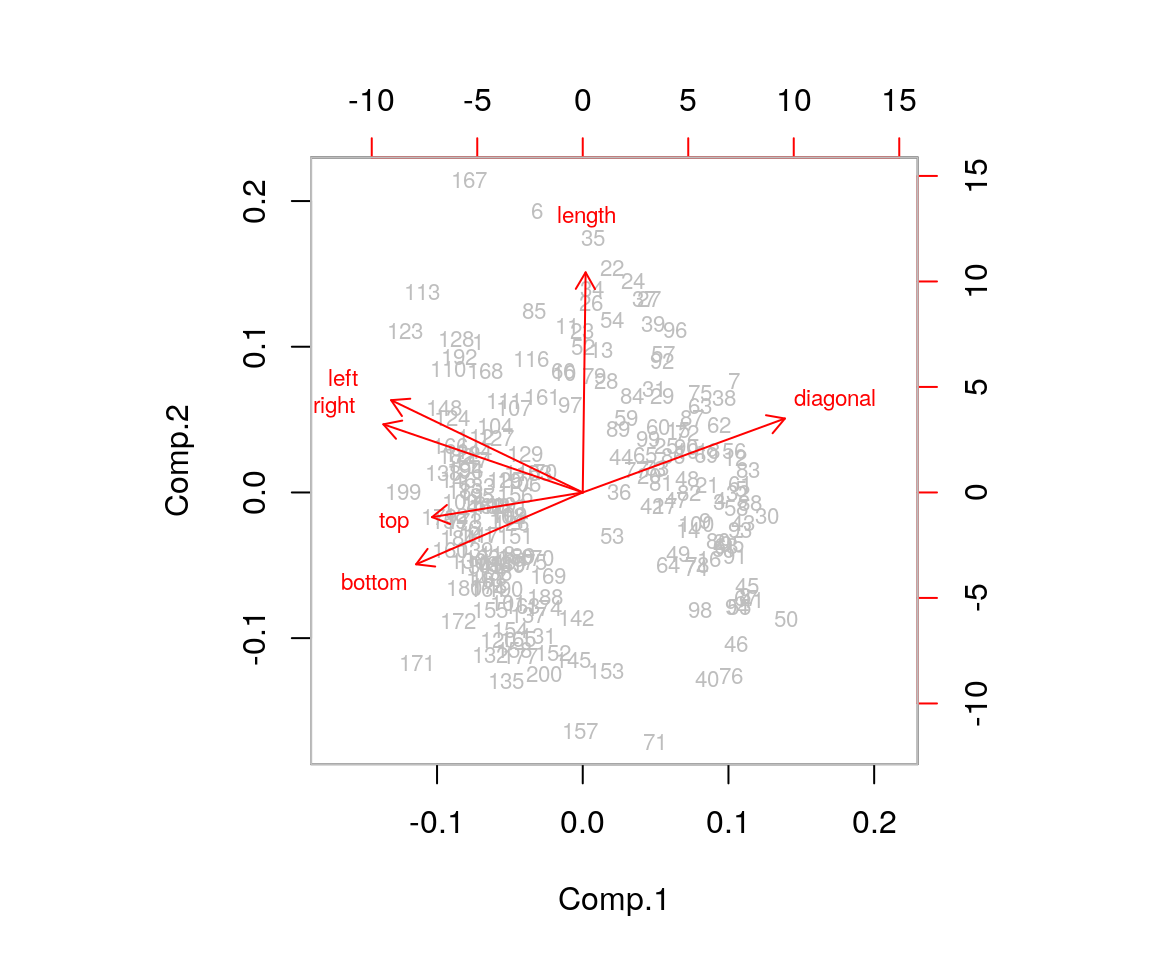
Possiamo ovviamente ottenere un grafico tridimensionale delle prime tre PC con la
funzione plot3d():
plot3d(pca_princomp$scores[, 1:3], col = as.integer(banknotes[, 7]) + 2, size = 5)
play3d(spin3d(axis = c(1, 1, 1), rpm = 15), duration = 10)Ora, un piccolo esercizio che dimostra le potenzialità di R legate alle sue caratteristiche di
linguaggi (anche) funzionale: rieseguiamo l’analisi separatamente per banconote genuine e contraffatte.
Al lettore l’esercizio di leggerne i risultati.
## [1] genuine counterfeit
## Levels: counterfeit genuine# Spezza il dataset originario in 2 dataset separati
bn_list <- split(x = banknotes,f = banknotes$type)
bn_list <- lapply(X = bn_list, FUN = function(x){x[,-7]})
# Produce la matrice di scatterplot per ciascun data frame della lista
lapply(X = bn_list,FUN = function(x){ggscatmat(x, columns = 1:6)})## $counterfeit
##
## $genuine
# Produce una lista con i risultati delle due analisi di componenti principali
pca_princomp <- lapply(X = bn_list,
FUN = function(x){princomp(x, cor = TRUE)})
# Produce il summary per entrambi i risultati
lapply(X = pca_princomp, FUN = summary)## $counterfeit
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.3914793 1.3284814 0.9941399 0.8822512 0.56754703
## Proportion of Variance 0.3227025 0.2941438 0.1647190 0.1297279 0.05368494
## Cumulative Proportion 0.3227025 0.6168463 0.7815653 0.9112932 0.96497810
## Comp.6
## Standard deviation 0.4584009
## Proportion of Variance 0.0350219
## Cumulative Proportion 1.0000000
##
## $genuine
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.4845355 1.3025778 0.9827302 0.76347839 0.57156088
## Proportion of Variance 0.3673076 0.2827848 0.1609598 0.09714988 0.05444697
## Cumulative Proportion 0.3673076 0.6500924 0.8110522 0.90820210 0.96264907
## Comp.6
## Standard deviation 0.47339788
## Proportion of Variance 0.03735093
## Cumulative Proportion 1.00000000# Mostra i loading con cutoff=0.1
invisible(lapply(X = pca_princomp,
FUN = function(x){
print(summary(x, loadings = TRUE), cutoff = .1)
}))## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.3914793 1.3284814 0.9941399 0.8822512 0.56754703
## Proportion of Variance 0.3227025 0.2941438 0.1647190 0.1297279 0.05368494
## Cumulative Proportion 0.3227025 0.6168463 0.7815653 0.9112932 0.96497810
## Comp.6
## Standard deviation 0.4584009
## Proportion of Variance 0.0350219
## Cumulative Proportion 1.0000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## length 0.434 0.178 0.848 0.137 0.190
## left 0.446 0.443 -0.310 -0.156 -0.688 -0.108
## right 0.399 0.479 -0.448 0.615 0.170
## bottom -0.526 0.445 -0.164 0.704
## top 0.397 -0.449 0.460 -0.233 -0.273 0.548
## diagonal -0.140 0.378 0.825 -0.168 -0.357
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.4845355 1.3025778 0.9827302 0.76347839 0.57156088
## Proportion of Variance 0.3673076 0.2827848 0.1609598 0.09714988 0.05444697
## Cumulative Proportion 0.3673076 0.6500924 0.8110522 0.90820210 0.96264907
## Comp.6
## Standard deviation 0.47339788
## Proportion of Variance 0.03735093
## Cumulative Proportion 1.00000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## length 0.450 0.479 0.742
## left 0.585 -0.107 -0.286 -0.700 0.269
## right 0.572 -0.456 0.676
## bottom 0.281 0.616 -0.280 -0.116 -0.669
## top -0.709 0.170 -0.673
## diagonal -0.206 0.315 0.809 -0.398 -0.165 -0.132# Produce la tabella delle correlazioni tra variabili e score delle componenti principali
lapply(X = 1:2,
FUN = function(x, bn, pca_princomp){
cor(bn[[x]], pca_princomp[[x]]$scores)
}, bn_list, pca_princomp)## [[1]]
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## length 0.6040179 0.2359174 0.08150875 0.74782493 0.07767695 0.08709660
## left 0.6200661 0.5889159 -0.30830023 -0.13750475 -0.39024330 -0.04949458
## right 0.5551664 0.6357583 0.05822711 -0.39510269 0.34928037 0.07815587
## bottom -0.7314361 0.5915182 -0.02339861 0.04135207 -0.09317513 0.32275120
## top 0.5527111 -0.5966905 0.45750911 -0.20515772 -0.15495164 0.25111072
## diagonal -0.1954408 0.5022568 0.82059065 0.01765530 -0.09538181 -0.16359269
##
## [[2]]
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## length 0.6673782 0.09638979 0.47048051 0.56617106 0.03711770 0.04512322
## left 0.8685205 -0.13980768 -0.04744941 -0.21847248 -0.39984407 0.12754986
## right 0.8494251 -0.04657390 0.07593872 -0.34808904 0.38626902 0.01309312
## bottom 0.4174559 0.80274705 -0.27472900 0.03409475 -0.06630537 -0.31669047
## top 0.1223100 -0.92334531 0.16752622 0.00424619 -0.05456601 -0.31845439
## diagonal -0.3055682 0.41077163 0.79551718 -0.30376457 -0.09408102 -0.06263385# Produce il grafico delle correlazioni tra le variabili e gli score delle componenti principali
lapply(X = 1:2,
FUN = function(x, bn, pca_princomp){
ggcorr(cbind(bn[[x]], pca_princomp[[x]]$scores), label = TRUE, cex = 2.5)
}, bn_list, pca_princomp)## [[1]]
##
## [[2]]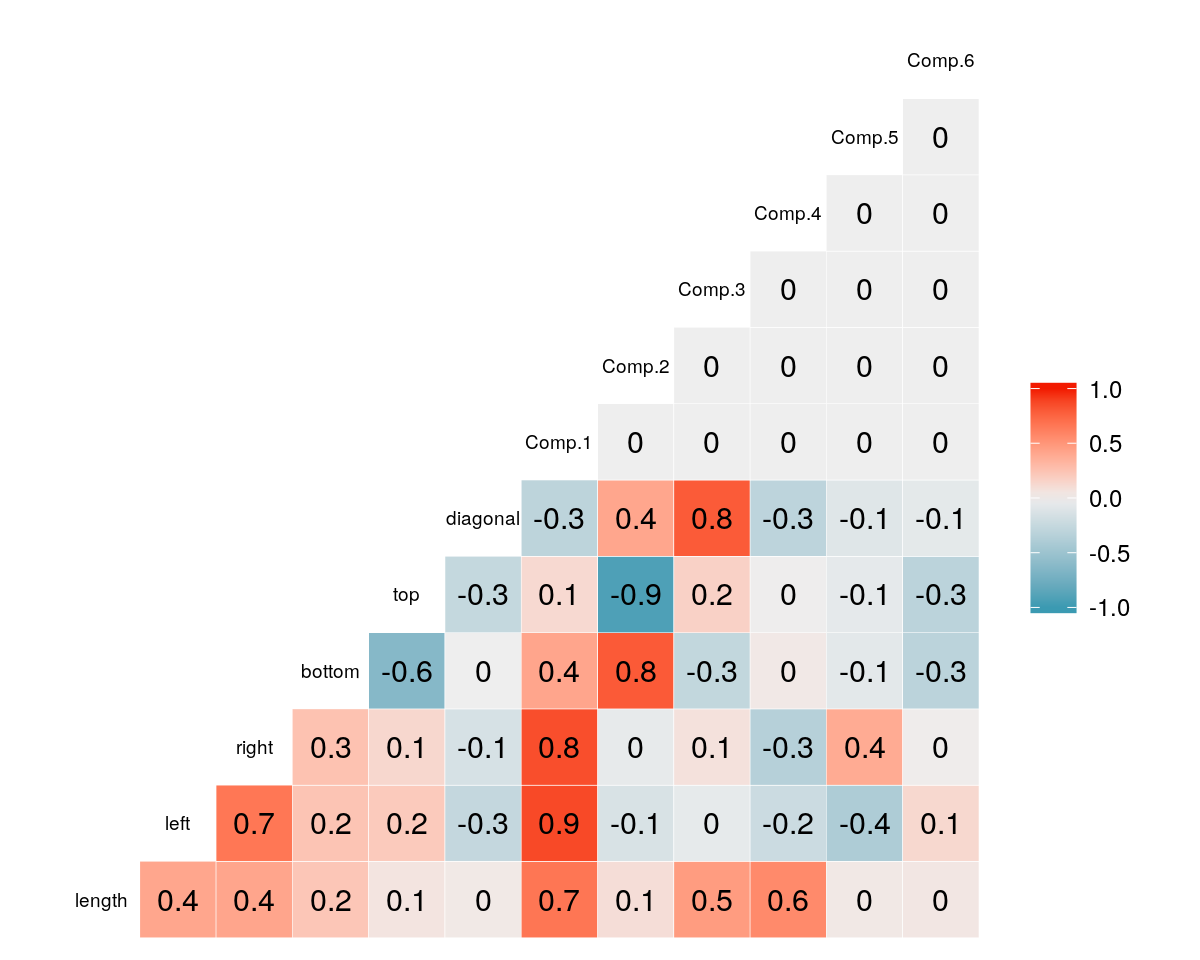
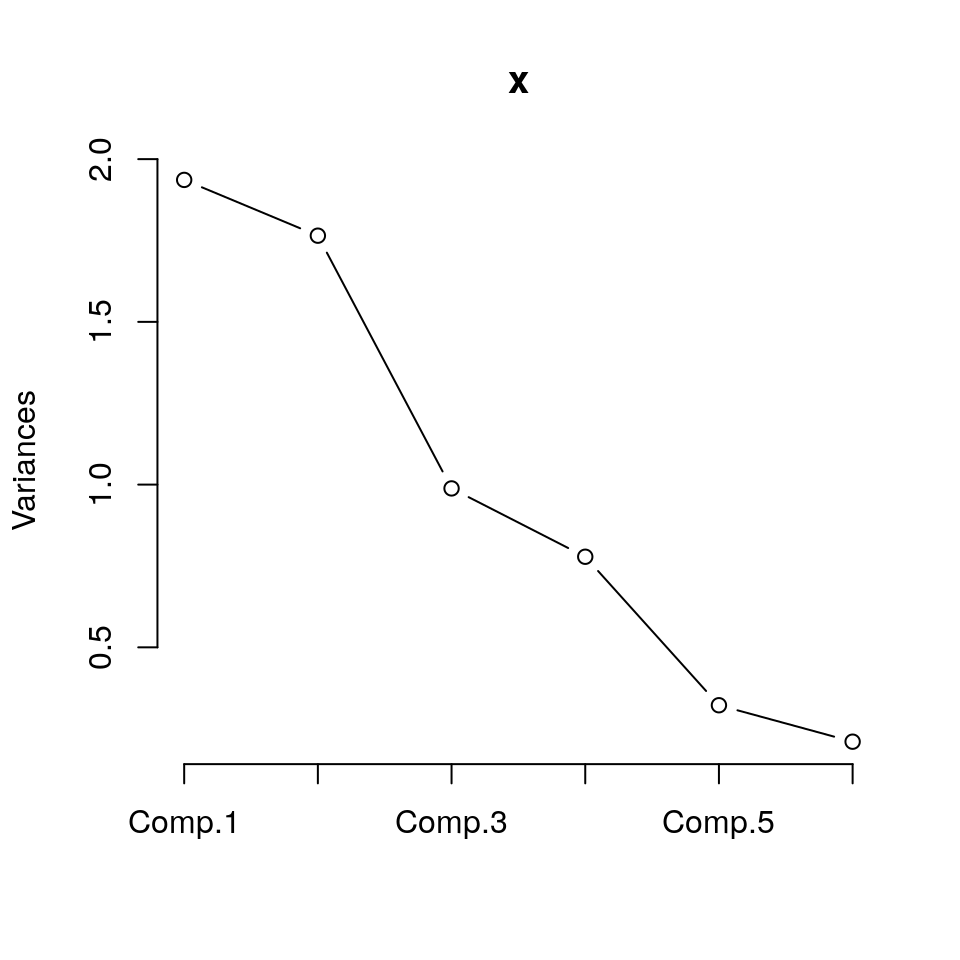
# Genera lo scree plot di entrambi i risultati di componenti principali
lapply(X = pca_princomp,
FUN = function(x){
plot(x, type = "lines")
})
## $counterfeit
## NULL
##
## $genuine
## NULL# Genera il grafico biplot delle prime due componenti per ciascuno dei risultati
lapply(X = pca_princomp,
FUN = function(x){
biplot(x, cex = c(.7, .7), col = c("black", "red"), choices = c("Comp.1","Comp.2"))
})

## $counterfeit
## NULL
##
## $genuine
## NULLI due tipi di banconota mostrano un pattern diverso nelle prime due componenti principali. Questa differenza potrebbe a sua volta aiutare nell’identificazione delle banconote contraffatte, per esempio usando qualche modello di classificazione sugli score.
4.2.4 Esempio: riproduzione di immagini
Questo è un esempio di applicazione avanzata, che però può permettere di comprendere come la PCA può essere vista come uno strumento per ridurre la quantità di dati richiesta per permettere di avere una informazione globale molto simile a quella del dato originario.
In questo esempio si proverà quindi ad analizzare una foto scattata durante una gara di velocità.
Si vedrà come si riesca a riprodurre l’immagine originale utilizzando una quantità di dati 4 volte più bassa rispetto alla dimensione iniziale.
L’esempio è complesso, e per questo non farò una analisi dettagliata del codice, altrimenti rischierei di dedicare tutto il materiale solo su questo.
Carichiamo le librerie e l’immagine da elaborare
## Loading required package: magrittr##
## Attaching package: 'imager'## The following object is masked from 'package:magrittr':
##
## add## The following objects are masked from 'package:stats':
##
## convolve, spectrum## The following object is masked from 'package:graphics':
##
## frame## The following object is masked from 'package:base':
##
## save.image##
## Attaching package: 'dplyr'## The following object is masked from 'package:GGally':
##
## nasa## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union##
## Attaching package: 'purrr'## The following object is masked from 'package:magrittr':
##
## set_names## 'cimg' num [1:1880, 1:1253, 1, 1] 0.345 0.345 0.353 0.361 0.365 ...
## [1] 1880 1253 1 1## x y value
## 1 1 1 0.3450980
## 2 2 1 0.3450980
## 3 3 1 0.3529412
## 4 4 1 0.3607843
## 5 5 1 0.3647059
## 6 6 1 0.3647059Ora prepariamo i dati per le analisi. La foto è organizzata come una matrice di punti con valori di grigio indicati da valori compresi tra 0 e 1.
## [1] 1880 1254## # A tibble: 5 x 5
## x `1` `2` `3` `4`
## <int> <dbl> <dbl> <dbl> <dbl>
## 1 1 0.345 0.337 0.333 0.322
## 2 2 0.345 0.341 0.337 0.325
## 3 3 0.353 0.349 0.341 0.333
## 4 4 0.361 0.357 0.349 0.341
## 5 5 0.365 0.361 0.353 0.345Applichiamo il calcolo delle compomenti principali
img_pca <- img_df %>%
dplyr::select(-x) %>%
prcomp(scale = TRUE, center = TRUE)
summary(img_pca)$importance[,1:100] ## PC1 PC2 PC3 PC4 PC5 PC6
## Standard deviation 14.26135 12.71393 10.58372 8.837683 8.657306 8.010189
## Proportion of Variance 0.16232 0.12901 0.08940 0.062330 0.059820 0.051210
## Cumulative Proportion 0.16232 0.29132 0.38072 0.443060 0.502870 0.554080
## PC7 PC8 PC9 PC10 PC11 PC12
## Standard deviation 7.669634 7.153169 5.777959 5.571306 5.222276 4.912522
## Proportion of Variance 0.046950 0.040840 0.026640 0.024770 0.021770 0.019260
## Cumulative Proportion 0.601030 0.641860 0.668510 0.693280 0.715040 0.734300
## PC13 PC14 PC15 PC16 PC17 PC18
## Standard deviation 4.58606 4.444328 4.166995 4.006884 3.845411 3.651224
## Proportion of Variance 0.01679 0.015760 0.013860 0.012810 0.011800 0.010640
## Cumulative Proportion 0.75109 0.766850 0.780710 0.793520 0.805330 0.815960
## PC19 PC20 PC21 PC22 PC23 PC24
## Standard deviation 3.350465 3.297699 3.105758 2.939769 2.898301 2.784955
## Proportion of Variance 0.008960 0.008680 0.007700 0.006900 0.006700 0.006190
## Cumulative Proportion 0.824920 0.833600 0.841300 0.848200 0.854900 0.861090
## PC25 PC26 PC27 PC28 PC29 PC30
## Standard deviation 2.761551 2.676325 2.586112 2.461598 2.349137 2.298719
## Proportion of Variance 0.006090 0.005720 0.005340 0.004840 0.004400 0.004220
## Cumulative Proportion 0.867180 0.872890 0.878230 0.883070 0.887470 0.891690
## PC31 PC32 PC33 PC34 PC35 PC36
## Standard deviation 2.230811 2.115945 2.051156 2.023795 1.988722 1.917489
## Proportion of Variance 0.003970 0.003570 0.003360 0.003270 0.003160 0.002930
## Cumulative Proportion 0.895660 0.899230 0.902590 0.905860 0.909020 0.911950
## PC37 PC38 PC39 PC40 PC41 PC42
## Standard deviation 1.869136 1.784015 1.737628 1.695754 1.682152 1.632889
## Proportion of Variance 0.002790 0.002540 0.002410 0.002290 0.002260 0.002130
## Cumulative Proportion 0.914740 0.917280 0.919690 0.921980 0.924240 0.926370
## PC43 PC44 PC45 PC46 PC47 PC48
## Standard deviation 1.619423 1.548456 1.519138 1.490396 1.448198 1.428246
## Proportion of Variance 0.002090 0.001910 0.001840 0.001770 0.001670 0.001630
## Cumulative Proportion 0.928460 0.930380 0.932220 0.933990 0.935670 0.937290
## PC49 PC50 PC51 PC52 PC53 PC54
## Standard deviation 1.41830 1.37679 1.353299 1.333692 1.291821 1.249729
## Proportion of Variance 0.00161 0.00151 0.001460 0.001420 0.001330 0.001250
## Cumulative Proportion 0.93890 0.94041 0.941870 0.943290 0.944630 0.945870
## PC55 PC56 PC57 PC58 PC59 PC60
## Standard deviation 1.234896 1.21806 1.200581 1.192832 1.173875 1.158883
## Proportion of Variance 0.001220 0.00118 0.001150 0.001140 0.001100 0.001070
## Cumulative Proportion 0.947090 0.94827 0.949420 0.950560 0.951660 0.952730
## PC61 PC62 PC63 PC64 PC65 PC66
## Standard deviation 1.139023 1.132972 1.09364 1.084617 1.08063 1.058226
## Proportion of Variance 0.001040 0.001020 0.00095 0.000940 0.00093 0.000890
## Cumulative Proportion 0.953770 0.954790 0.95574 0.956680 0.95762 0.958510
## PC67 PC68 PC69 PC70 PC71 PC72
## Standard deviation 1.044226 1.022985 1.008718 0.9937964 0.9784785 0.9579364
## Proportion of Variance 0.000870 0.000840 0.000810 0.0007900 0.0007600 0.0007300
## Cumulative Proportion 0.959380 0.960210 0.961030 0.9618200 0.9625800 0.9633100
## PC73 PC74 PC75 PC76 PC77 PC78
## Standard deviation 0.9496314 0.9407888 0.925364 0.9170252 0.8976748 0.8851248
## Proportion of Variance 0.0007200 0.0007100 0.000680 0.0006700 0.0006400 0.0006300
## Cumulative Proportion 0.9640300 0.9647400 0.965420 0.9660900 0.9667400 0.9673600
## PC79 PC80 PC81 PC82 PC83 PC84
## Standard deviation 0.8816077 0.8762076 0.855872 0.8450853 0.8357144 0.8275234
## Proportion of Variance 0.0006200 0.0006100 0.000580 0.0005700 0.0005600 0.0005500
## Cumulative Proportion 0.9679800 0.9685900 0.969180 0.9697500 0.9703100 0.9708500
## PC85 PC86 PC87 PC88 PC89
## Standard deviation 0.8147506 0.7955843 0.7914764 0.7865595 0.7803561
## Proportion of Variance 0.0005300 0.0005100 0.0005000 0.0004900 0.0004900
## Cumulative Proportion 0.9713800 0.9718900 0.9723900 0.9728800 0.9733700
## PC90 PC91 PC92 PC93 PC94 PC95
## Standard deviation 0.7682683 0.7571979 0.7535708 0.736888 0.7301807 0.7168217
## Proportion of Variance 0.0004700 0.0004600 0.0004500 0.000430 0.0004300 0.0004100
## Cumulative Proportion 0.9738400 0.9743000 0.9747500 0.975180 0.9756100 0.9760200
## PC96 PC97 PC98 PC99 PC100
## Standard deviation 0.7130543 0.7020036 0.6882716 0.68169 0.6714046
## Proportion of Variance 0.0004100 0.0003900 0.0003800 0.00037 0.0003600
## Cumulative Proportion 0.9764200 0.9768200 0.9771900 0.97757 0.9779300pca_tidy <- tidy(img_pca, matrix = "pcs")
pca_tidy %>%
ggplot(aes(x = PC, y = percent)) +
geom_line() +
ggtitle("Scree plot") +
labs(x = "Component Principale", y = "Varianza Spiegata") 
Ora costruiamo una funzione che “inverte” l’operazione di estrazione delle componenti principali:
prende le prime n_comp componenti più importanti e quindi ricostruisce l’immagine originale usando
solo quelle compomenti.
reverse_pca <- function(n_comp = 20, pca_object = img_pca){
## pca_object è un oggetto creato dalla funzione prcomp() di R base.
## Moltiplica la matrice dei dati ruotati per la trssposta della matrice
## degli autovettori (cioè i pesi delle componenti) per tornare ad una matrice
## dei valori dei dati originali
recon <- pca_object$x[, 1:n_comp] %*% t(pca_object$rotation[, 1:n_comp])
## Inverte la centratura e la scalatura applicata da prcomp()
if(all(pca_object$scale != FALSE)){
## Riscala con il reciproco del fattore di scala, cioè torna
## al range iniziale.
recon <- scale(recon, center = FALSE, scale = 1/pca_object$scale)
}
if(all(pca_object$center != FALSE)){
## Rimuove le centrature applicate sui dati
recon <- scale(recon, scale = FALSE, center = -1 * pca_object$center)
}
## Conferte il tutto in un data frame che sarà semplice da trasformare in formato long
## (poiché questo è il formato che la libreria imager vuole quando
## si tracciano le immagini con ggplot)
recon_df <- data.frame(cbind(1:nrow(recon), recon))
colnames(recon_df) <- c("x", 1:(ncol(recon_df)-1))
## Ritorna i dati in formato lungo
recon_df_long <- recon_df %>%
tidyr::pivot_longer(cols = -x,
names_to = "y",
values_to = "value") %>%
mutate(y = as.numeric(y)) %>%
arrange(y) %>%
as.data.frame()
recon_df_long
}A questo punto usiamo la funzione costruita sopra e la applichiamo provando ad usare 2, 10, 50, 150, 300 componenti, e confrontiamo quete immagini ricostruite con quella originale.
n_pcs <- c(2, 10, 50, 150, 300, 2)
names(n_pcs) <- paste("Prime", n_pcs, "Componenti", sep = "_")
## map reverse_pca()
recovered_imgs <- map_dfr(n_pcs[1:5],
reverse_pca,
.id = "pcs") %>%
mutate(pcs = stringr::str_replace_all(pcs, "_", " ")) %>%
bind_rows(bind_cols(pcs=rep("Originale",nrow(img_df_long)), img_df_long)) %>%
mutate(pcs = factor(pcs, levels = c(unique(pcs)[1:5], "Originale"), ordered = TRUE))
p <- ggplot(data = recovered_imgs,
mapping = aes(x = x, y = y, fill = value))
p_out <- p + geom_raster() +
scale_y_reverse() +
scale_fill_gradient(low = "black", high = "white") +
facet_wrap(~ pcs, ncol = 2) +
guides(fill = FALSE) +
labs(title = "Ricostruzione immagine 1880x1254 px \nda Analisi Componenti Principali dei suoi pixel") +
theme(strip.text = element_text(face = "bold", size = rel(1)),
plot.title = element_text(size = rel(1.2)))
4.3 Analisi Fattoriale Esplorativa (Exploratory Factor Analysis: EFA)
L’analisi fattoriale è collegata all’analisi delle componenti princiali, ma i due metodi hanno
obiettivi diversi. L’analisi delle componenti principali cerca di identificare comninazioni lineari ortogonali
delle variabili originarie, da usare a fine descrittivo o anche per sostituire le variabili originarie
con un numero più piccolo di variabili (“sintetiche”) ortogonali.
In contrasto, l’analisi fattoriale rappresenta un modello per i dati, e come tale è più elaborata.
Il modello di analisi fattoriale ipotizza che le variabili originarie possano essere modellate come
combinazioni lineari di un insieme ridotto di variabili casuali “latenti” non osservabili,
chiamate fattori comuni, insieme a un termine di errore, noto anche come
fattore specifico (per avere più dettagli sulla specificazione del modello
si veda Johnson and Wichern, Applied Multivariate Statistical Analysis, 6th edition, Pearson, 2014).
I coefficienti delle combinazioni lineari sono chiamati loading fattoriali.
Le variabilità dele variabili originarie spiegate dal set di fattori comuni
sono chiamate comunalità, mentre le variabilità non spiegate sono chiamate
unicità o varianze specifiche.
4.3.1 Esempio: Uso di sostanze alteranti
L’esempio si basa sul dataset druguse, che contiene informazioni sull’uso di sostanze alteranti su un campione di 1,634 studenti tra la settima e la nona classe in 11 scuole della grande area metropolitana di Los Angeles. Ogni partecipante ha completato un questionario sul numero di volte che ha fatto uso di una particolare sostanza, più o meno alterante. Le sostanze su interessate allo studio sono le seguenti:
- sigarette;
- birra;
- vino;
- liquore;
- cocaina;
- tranquillanti;
- farmaci da banco stimolanti;
- eroina e altri oppiacei;
- mariuana;
- hashish;
- inalanti (colla, benzine, ecc.);
- allucinogeni (LSD, mescalina, ecc.);
- amfetamine stimolanti.
Le risposte sono state raccolte su una scala su 5 punti: mai provata, solo una volta, qualche volta, molte volte e regolarmente.
Le correlazioni tra i tassi di utilizzo delle 13 sostanze sono rappresentati graficamente usando la funzione levelplot() del package lattice con una funzione di “panel” piuttosto complessa (sono riportati i coefficienti di correlazione moltiplicati all’interno delle ellissi):
panel.corrgram <- function(x, y, z, subscripts, at, level = 0.9, label = FALSE, ...) {
#require("ellipse", quietly = TRUE)
x <- as.numeric(x)[subscripts]
y <- as.numeric(y)[subscripts]
z <- as.numeric(z)[subscripts]
zcol <- level.colors(z, at = at, ...)
for (i in seq(along = z)) {
ell <- ellipse(z[i], level = level, npoints = 50, scale = c(.2, .2),
centre = c(x[i], y[i]))
panel.polygon(ell, col = zcol[i], border = zcol[i], ...)
}
if (label) {
panel.text(x = x, y = y, lab = 100 * round(z, 2), cex = 0.8,
col = ifelse(z < 0, "white", "black"))
}
}
print(levelplot(druguse, at = do.breaks(c(-1.01, 1.01), 20),
xlab = NULL, ylab = NULL, colorkey = list(space = "top"),
scales = list(x = list(rot = 90)), panel = panel.corrgram, label = TRUE))
Si noti come la struttura di correlazioni non sia molto forte. Perché funzioni,
l’analisi fattoriale richiede un livello minimo di correlazione tra le variabili analizzate.
Sono stati sviluppati proprio per questo alcuni test per verificare se esiste un livello di
correlazione sufficientemente elevato per eseguire l’analisi fattoriale:
- Statistica di Kaiser–Meyer–Olkin: misura la proporzione di variabilità entro le variabili standardizzate analizzate che è condivisa nella comunalità, e che quindi può essere dovuta a sottostanti fattori; valori della statistica KMO inferiori a 0.50 indicano che l’analisi fattoriale potrebbe non essere appropriata.
- Test di Bartlett: test l’ipotesi nulla che la matrice di correlazione possa essere una matrice identità, cioè, che le variabili possano essere incorrelate nella realtà. Ovviamente, se il test di Bartlett “dice” che la matrice di correlazione può essere una matrice Identità, allora una analisi fattoriale potrebbe essere inutile.
Entrambi questi strumenti sono disponibili all’interno del package psych:
## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = druguse)
## Overall MSA = 0.87
## MSA for each item =
## cigarettes beer wine
## 0.89 0.84 0.83
## liquor cocaine tranquillizers
## 0.88 0.87 0.87
## drug store medication heroin marijuana
## 0.88 0.88 0.87
## hashish inhalants hallucinogenics
## 0.88 0.91 0.85
## amphetamine
## 0.86## $chisq
## [1] 6592.802
##
## $p.value
## [1] 0
##
## $df
## [1] 78Poiché entrambi gli strumenti forniscono risultati ragionevoli, procederemo con l’analisi
fattoriale. Il modello di analisi fattoriale può essere stimato in R uando la funzione
factanal(), che implementa un approccio di massima verosimiglianza per la stima dei loading
fattoriali:
##
## Call:
## factanal(factors = 2, covmat = druguse, n.obs = 1634, rotation = "none")
##
## Uniquenesses:
## cigarettes beer wine
## 0.635 0.367 0.447
## liquor cocaine tranquillizers
## 0.405 0.774 0.552
## drug store medication heroin marijuana
## 0.876 0.764 0.540
## hashish inhalants hallucinogenics
## 0.577 0.704 0.604
## amphetamine
## 0.430
##
## Loadings:
## Factor1 Factor2
## cigarettes 0.570 -0.200
## beer 0.667 -0.435
## wine 0.612 -0.422
## liquor 0.708 -0.306
## cocaine 0.321 0.351
## tranquillizers 0.514 0.429
## drug store medication 0.277 0.216
## heroin 0.310 0.374
## marijuana 0.677
## hashish 0.616 0.207
## inhalants 0.474 0.266
## hallucinogenics 0.412 0.476
## amphetamine 0.604 0.454
##
## Factor1 Factor2
## SS loadings 3.783 1.542
## Proportion Var 0.291 0.119
## Cumulative Var 0.291 0.410
##
## Test of the hypothesis that 2 factors are sufficient.
## The chi square statistic is 478.08 on 53 degrees of freedom.
## The p-value is 9.79e-70L’ output di una analisi fattoriale è molto simile a quello di una PCA e può essere interpretato in maniera simile: scegliendo due fattori, siamo in grado di spiegare circa il 41% della varianza/covarianza complessiva delle variabili originarie. Comunque, guardando i loading fattoriali (che ora forniscono la correlazione con ciascuna delle variabili originarie) non siamo in grado di interpretarli chiaramente. Infine, i valori di unicità segnalano che la gran parte della variabilità per molte delle variabili originarie resta non spiegata. Queste conclusioni suggeriscono che probabilmente questa prima soluzione non è appropriata.
Se è accettabile l’ipotesi di normalità multivariata, per determinare un numero ragionevole
di fattori da estrarre, possiamo usare il test di rapporto di verosimiglianza
fornito dalla funzione factanal(), per verificare l’ipotesi che un dato numero di fattori
sia sufficiente a spiegare le relazioni tra i dati:
pval <- sapply(1:6, function(nf)
factanal(covmat = druguse, factors = nf, n.obs = 1634)$PVAL)
names(pval) <- sapply(1:6, function(nf) paste0("nf = ", nf))
pval## nf = 1 nf = 2 nf = 3 nf = 4 nf = 5 nf = 6
## 0.000000e+00 9.786000e-70 7.363910e-28 1.794578e-11 3.891743e-06 9.752967e-02Questi valori suggeriscono che la soluzione con sei fattori fornisce una adeguata descrizione. I risultati della soluzione con sei fattori sono ottenuti come:
##
## Call:
## factanal(factors = 6, covmat = druguse, n.obs = 1634, rotation = "none")
##
## Uniquenesses:
## cigarettes beer wine
## 0.563 0.368 0.374
## liquor cocaine tranquillizers
## 0.412 0.681 0.522
## drug store medication heroin marijuana
## 0.785 0.669 0.318
## hashish inhalants hallucinogenics
## 0.005 0.541 0.620
## amphetamine
## 0.005
##
## Loadings:
## Factor1 Factor2 Factor3 Factor4 Factor5 Factor6
## cigarettes 0.325 0.523 -0.225
## beer 0.306 0.708 0.130 0.126
## wine 0.253 0.711 0.220
## liquor 0.391 0.647
## cocaine 0.341 0.424 0.140
## tranquillizers 0.546 0.325 -0.148 0.223
## drug store medication 0.235 0.343 -0.168
## heroin 0.316 0.448 0.129
## marijuana 0.544 0.441 0.156 -0.406
## hashish 0.840 0.538
## inhalants 0.412 0.166 0.425 -0.274
## hallucinogenics 0.518 0.275 -0.126 0.106
## amphetamine 0.869 -0.489
##
## Factor1 Factor2 Factor3 Factor4 Factor5 Factor6
## SS loadings 3.180 1.937 0.873 0.643 0.309 0.196
## Proportion Var 0.245 0.149 0.067 0.049 0.024 0.015
## Cumulative Var 0.245 0.394 0.461 0.510 0.534 0.549
##
## Test of the hypothesis that 6 factors are sufficient.
## The chi square statistic is 22.41 on 15 degrees of freedom.
## The p-value is 0.0975Per meglio interpretare i fattori stimati, possiamo applicare una rotazione dei
loading fattoriali. Una rotazione molto popolare è la varimax, finalizzata a produrre
fattori con elevata correlazione con un insieme piccolo di variabili
e correlazioni piccole o nulle con gli altri insiemi. Possiamo applicare una
rotazione direttamente dalla funzione factanal() fornendo il nome del metodo di
rotazione scelto al parametro rotation:
du_fa6_rot <- factanal(covmat = druguse, n.obs = 1634, factors = 6,
rotation = "varimax")
du_fa6_rot##
## Call:
## factanal(factors = 6, covmat = druguse, n.obs = 1634, rotation = "varimax")
##
## Uniquenesses:
## cigarettes beer wine
## 0.563 0.368 0.374
## liquor cocaine tranquillizers
## 0.412 0.681 0.522
## drug store medication heroin marijuana
## 0.785 0.669 0.318
## hashish inhalants hallucinogenics
## 0.005 0.541 0.620
## amphetamine
## 0.005
##
## Loadings:
## Factor1 Factor2 Factor3 Factor4 Factor5 Factor6
## cigarettes 0.494 0.407 0.110
## beer 0.776 0.112
## wine 0.786
## liquor 0.720 0.121 0.103 0.115 0.160
## cocaine 0.519 0.132 0.158
## tranquillizers 0.130 0.564 0.321 0.105 0.143
## drug store medication 0.255 0.372
## heroin 0.532 0.101 0.190
## marijuana 0.429 0.158 0.152 0.259 0.609 0.110
## hashish 0.244 0.276 0.186 0.881 0.194 0.100
## inhalants 0.166 0.308 0.150 0.140 0.537
## hallucinogenics 0.387 0.335 0.186 0.288
## amphetamine 0.151 0.336 0.886 0.145 0.137 0.187
##
## Factor1 Factor2 Factor3 Factor4 Factor5 Factor6
## SS loadings 2.301 1.415 1.116 0.964 0.676 0.666
## Proportion Var 0.177 0.109 0.086 0.074 0.052 0.051
## Cumulative Var 0.177 0.286 0.372 0.446 0.498 0.549
##
## Test of the hypothesis that 6 factors are sufficient.
## The chi square statistic is 22.41 on 15 degrees of freedom.
## The p-value is 0.0975Le sostanze che “pesano” di più sul primo fattore sono sigarette, birra, vino, liquore e marjuana; potremmo etichettare il fattore come “uso sociale/leggero”. Cocaina, tranquillanti e eroina pesano maggiormente sul secondo factore; l’etichetta ovvia per il fattore potrebbe essere “uso droghe pesanti”. Il terzo fattore è essenzialmente legato all’uso di amfetamina, mentre il quarto all’uso di hashish. I fattori rimanenti pesano principalmente su una sola variabile.
Come per la PCA, possiamo richiedere gli scores fattoriali EFA aggiungendo l’argomento
scores; gli score possono essere prodotti solo se è fornita una matrice di dati (non di varianze/covarianze).
Gli score sono accessibili attraverso l’elemento scores della lista ritornata dalla funzione.
4.4 Alcuni cenni di teoria
4.4.1 PCA
L’obiettivo dell’Analisi delle Componenti Principali è trovare le combinazioni lineari delle variabili analizzate che ritornano la variabilità più elevata, dati i dati.
Supponiamo che i dati contengano valori numerici per \(p\) variabili su \(n\) casi. Chiamiamo \(X\) la matrice dei dati \((n \times p)\).
Supponiamo quindi la generica riga di \(X\), indicata con \(\underline{x}\) , sia una realizzazione casuale dalla stessa distribuzione casuale multivariata, con matrice di varianza/covarianza indicata con \(\Sigma\).
Ora, vogliamo trovare la combinazione lineare
\[
z= \underline{a}^T\underline{x}
\]
Tale per cui \(Var(z)\) sia massimo. Poiché questo problema non ha una soluzione unica, vincoleremo il problema entro vettori dei pesi di norma unitaria (\(\underline{a}^T\underline{a}=1\)).
Comunque, si può dimostrare che \(Var(z)= \underline{a}^T \Sigma \underline{a}\), e quindi che il problema qui sopra può essere espresso come un problema di massimizzazione vincolata: \[ \max_{\begin{matrix} \underline{a}\\ s.t.:\underline{a}^T\underline{a}=1 \end{matrix} } \left\{\underline{a}^T \Sigma \underline{a}\right\} \\ \]
Questo porblema di ottimo può essere risolto usando i moltiplicatori di Lagrange, e la soluzione è data dai vettori \(\underline{a}\) tali che \[ (\Sigma - \lambda \underline{I}) \underline{a}=\underline{0} \]
cioè, la soluzione del problema è data dagli autovettori (ortonormali) di \(\Sigma\).
Il numero di autovalori non nulli \(\lambda\) è uguale a \(g = rank(X) \le p\), e la loro somma è uguale alla somma degli elementi sulla diagonale di \(\Sigma\), cioè, delle varianza di \(\underline{x}\). Ad ogni autovalore corrisponde un autovettore \(\underline{a}\) che è anche una soluzione dell’equazione qui sopra.
Come risultato di questi calcoli otteniamo una fattorizzazione di \(\Sigma\) come:
\[
\Sigma = \Gamma \Lambda \Gamma^T
\]
Dove \(\Gamma\) è la matrice \((p \times g)\) risultante dall’accostamento fianco a fianco degli autovettori \(\underline{a}\), e \(\Lambda\) è la matrice diagonale \((g \times g)\) contenente i corrispondenti \(g\) autovalori (\(\lambda\)) in ordine decrescente di dimensione.
I vettori \(\underline{a}\) sono chiamati loading, mentre gli \(\underline{z}\) sono chiamati score. Di conseguenza, se ci sono \(p\) autovalori non nulli, allora ci sono anche \(p\) distinti \(\underline{z}\), uno per ogin soluzione, e quindi possiamo pensare ad un vettore degli \(\underline{z}\): \(\underline{z}=\Gamma^T \underline{x}\).
La matrice di varianza/covarianza di \(\underline{z}\) è quindi: \[ Var\{\underline{z}\}=\Gamma^T Var\{\underline{x}\}\Gamma=\Gamma^T \Gamma \Lambda \Gamma^T \Gamma=\Lambda \]
Ovviamente, \(\Sigma\) è usualmente sconosciuta. In questi casi, possiamo usare \(S\), la stima campionaria di \(\Sigma\), al posto di \(\Sigma\) stesso.
In ogni modo, dati questi risultati, e data una matrice di dati \(X\), possiamo ottenere una matrice di score campionari \(Z\) come: \[ Z = X \Gamma \] Dove \(\Gamma\) è la matrice degli autovettori ottenuti da \(S\).
La matrice di varianza/covarianza dsi \(Z\), ovviamente, è \(\Lambda\), dove \(\Lambda\) è la matrice diagonale ottenuta fattorizzando \(S\) come visto sopras.
4.4.2 EFA
EFA è molto simile alla PCA sia negli obiettivi che nei metodi usati per ottenere i risultati.
Tuttavia, possiamo notare che in questo paragrafo le notazioni e i simboli sono diversi dalle notazioni e simboli usati per descrivere la PCA.
EFA ipotizza che il singolo vettore di dati , \(\underline{x}\), provenga da una distrubzione multivariata con media \(\underline{\mu}\) e matrice di varianza/covarianza \(\Sigma\), e che valga il seguente modello:
\[
\underline{x} = \Gamma \underline{f} + \underline{\varepsilon} + \underline{\mu}
\]
dove \(\Gamma\) è una matrice \((p \times g)\) di costati (i loading fattoriali), e \(\underline{f}\) e \(\underline{\varepsilon}\) sono, rispettivamente, i vettori casuali \((g \times 1)\) e \((p \times 1)\) dei fattori comuni e specifici, per cui:
\[
E\{\underline{f}\}=\underline{0}; Var\{\underline{f}\}=\underline{I}
\]
\[
E\{\underline{\varepsilon}\}=\underline{0}; Var\{\underline{\varepsilon}\}=\Lambda=diag(\lambda_1,\cdots,\lambda_g)
\]
e
\[
Cov\{\underline{f},\underline{\varepsilon}\}=\underline{0}
\]
Quindi, tutti i fattori sono incorrelati tra loro ed inoltre i fattori \(\underline{f}\) sono tutti standardizzati per avere varianza pari a 1.
Talvolta è anche utile supporre che \(\underline{f}\) e \(\underline{\varepsilon}\) (e quindi \(\underline{x}\)) siano distribuiti come normali multivariate.
La validità del modello a \(g\) fattori può essere espressa in termini di una semplice condizione su \(\Sigma\): \[ \Sigma=\Gamma \Gamma^T + \Lambda \]
Vale anche l’opposto. Se \(\Sigma\) può essere scomposto nella forma qui sopra, allora il modello a \(g\) fattori vale per \(\underline{x}\).
4.4.2.1 Non unicità dei loading fattoriali
Dati i risultati qui sopra, si può arguire che non ci sia una sola soluzione per il modello EFA. Infatti, se \(\Phi\) è una matrice di rotazione (cioè, una tale per cui \(\Phi \Phi^T=\underline{I}\)), allora \(\underline{x}\) può essere scritto come: \[ \underline{x} = (\Gamma\Phi) (\Phi^T \underline{f}) + \underline{\varepsilon} + \underline{\mu} \] Poiché il vettore casuale \(\Phi^T \underline{f}\) soddisfa la condizione indicata prima relativa ai fattori e per \(\Sigma\) vale: \[ \Sigma=(\Gamma\Phi)(\Gamma\Phi)^T + \Lambda = \Gamma\Gamma^T + \Lambda \] Allora il modello con \(g\) fattori è ancora valido con i nuovi fattori \((\Phi^T \underline{f})\) e i nuovi loading fattoriali \((\Gamma\Phi)\).
Questo da la possibilità al ricercatore di trovare alcune strategie di rotazione sui loading per rendere le soluzioni fattoriali più facilmente interpretabili.