Capitolo 12 Analisi Discriminante Lineare e Quadratica (LDA e QDA)

12.1 Analisi Discriminante Lineare (LDA)

Nella LDA, la distribuzione dei predittori \(X\) è modellata separatamente in ciascuna delle classi della variabile di risposta (cioè. \(Y\)), e quindi, tramite il teorema di Bayes, è usata per convertire queste distribuzioni in stime per \(Pr(Y = k|X = x)\), chiamate “probabilità a posteriori”. Più specificatamente, il teorema di Bayes permette di ottenere le probabilità a posteriori combinando probabilità “a priori” con l’evidenza proveniente dai dati. Ogni osservazione è quindi assegnata alla clase con la più elevata probabiltà a posteriori.

Alternativamente, seguedo la formulazione di Fisher, l’obiettivo della LDA può anche essere espresso come trovare una combinazione lineare \(w\) dei predittori che massimizza la separazione tra i centri dei dati, minimizzando contestualmente la variabilità all’interno di ciascun gruppo di dati, dopo la proiezione con \(w\). Ricordando che la prima componente principale rappresenta la direzione che massimizza la varianza dei punti proiettati, la differenza principale tra PCA e LDA è che la prima opera con dati non etichettati, e quindi cerca di massimizzare la varianza, la seconda opera con dati etichettati (gruppo d’appartenenza) e cerc di massimizzare la discriminazione tra le classi.

L’assunto in LDA è che le matrici di covarianza (o varianza/covarianza) dei predittori all’inteno delle diverse classi sono uguali.

In LDA i parametri ignoti delle distribuzioni (supposte normali) multivariate di ogni classe devono essere prima stimati. Queste stime sono quindi usate per trovare le soglie di decisione con cui assegnare le osservazioni alle diverse classi. Queste soglie sono determinate utilizzando le cosiddette “funzioni discriminanti linari di Fisher”.

Per eseguire la LDA sui dati delle carte di credto, possiamo usare la funzione lda() del package MASS. Questa funzione richiede di impostare una formula che specifica la risposta categoriale ed i predittori da usare, il data frame contenente i dati, ed una serie di altri argomenti opzionali, quale il metodo usato per la stima e le probabilità a priori per ogni classe (se l’argomento della probabilità a priori non è specificato, sono usate le proporzioni delle classi dell’insieme di osservazioni di training):

12.1.1 Esempio: Default carte di credito

Proveremo quindi l’LDA sul dataset Default:

library(MASS)

data(Default, package = "ISLR")
summary(Default)

##  default    student       balance           income     
##  No :9667   No :7056   Min.   :   0.0   Min.   :  772  
##  Yes: 333   Yes:2944   1st Qu.: 481.7   1st Qu.:21340  
##                        Median : 823.6   Median :34553  
##                        Mean   : 835.4   Mean   :33517  
##                        3rd Qu.:1166.3   3rd Qu.:43808  
##                        Max.   :2654.3   Max.   :73554

res <- lda(default ~ student + balance, data = Default)
res

## Call:
## lda(default ~ student + balance, data = Default)
## 
## Prior probabilities of groups:
##     No    Yes 
## 0.9667 0.0333 
## 
## Group means:
##     studentYes   balance
## No   0.2914037  803.9438
## Yes  0.3813814 1747.8217
## 
## Coefficients of linear discriminants:
##                     LD1
## studentYes -0.249059498
## balance     0.002244397

L’output (un oggetto di classe lda) mostra che i non studenti con valori di balance (credito residuo medio) più elevati sono più propensi da non pagare. Per assegnare (prevedere) le osservazioni nelle due classi, useremo la funzione predict():

default_hat <- predict(res)$class

Ed ora possiamo stabilire la bontà della classificazione:

table(default_hat, Default$default)

##            
## default_hat   No  Yes
##         No  9644  252
##         Yes   23   81

Elementi sulla diagonale principale della matrice rappresentano individui il cui stato di default è correttamente previsto, mentre elementi fuori della diagonale rappresentano individui mal classificati. Quindi, il modello LDA adattato sulle 10000 osservazioni ottiene un tasso d’errore di (23 + 252)/10,000 = 0.0275, cioè 2.75%. Questo sembra essere un tasso d’errore basso, tuttavia vanno notati un paio problemi:

Primo, i tassi d’errore per le osservazioni uate nella stima del modello sono tipicamente più bassi di quelli che si ottengono applicando il modello su un secondo insieme di individui. La ragione di ciò è che i parametri del modello sono stimati specificatamente per “descrivere bene” i dati usati per il training;
Secondo, poiché solo il 3.33% degli individui del campione di training è andato in default, un classificatore semplice ma poco utile che preveda sempre che un individuo non andrà in default, indipendentemente dallo stato delle sue variabili esplicative, otterrà comunque un tasso d’errore pari a 3.33%. In altre parole, il classificatore “banale” otterrà un tasso d’errore che sarà solo di poco più alto del tasso d’errore LDA ottenuto sui dati di training.

Quindi, dei 333 individui andati in default, 252 (o 252/333 = 0.757) non sono stati individuati da LDA. Mentre il tasso d’errore complessivo è basso, il tasso d’errore tra gli individui che sono andati in default è molto alto. Dal punto di vista di una azienda di credito che cerca di identificare individui ad alto rischio, un tasso d’errore del 75.7% tra individui che sono andati in default potrebbe essere inaccettabile.
Un altro modo per stabilire le performance specifiche di classe usa i concetti di “sensitivity” e “specificity” (sensibililtà e specificità). La sensibilità è la percentuale di veri defaulter che sono stati individuati (nel nostro esempio, 81/(252 + 81) = 0.243). La specificità è la percentuale di non-defaulter che sono stati correttamente identificati (nel nostro esempio, 9644/(9644 + 23) = 0.998).

Nel package caret è presente la funzione confusionMatrix() che calcola automaticamente la matrice di confusione ed altre statistiche collegate al problema della classificazione:

library(caret)

confusionMatrix(data = default_hat, reference = Default$default,
                positive = "Yes")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction   No  Yes
##        No  9644  252
##        Yes   23   81
##                                           
##                Accuracy : 0.9725          
##                  95% CI : (0.9691, 0.9756)
##     No Information Rate : 0.9667          
##     P-Value [Acc > NIR] : 0.0004973       
##                                           
##                   Kappa : 0.3606          
##                                           
##  Mcnemar's Test P-Value : < 2.2e-16       
##                                           
##             Sensitivity : 0.2432          
##             Specificity : 0.9976          
##          Pos Pred Value : 0.7788          
##          Neg Pred Value : 0.9745          
##              Prevalence : 0.0333          
##          Detection Rate : 0.0081          
##    Detection Prevalence : 0.0104          
##       Balanced Accuracy : 0.6204          
##                                           
##        'Positive' Class : Yes             
##

Per comprendre perché LDA ottiene risultati così scarsi (soprattutto dal punto di vista della sensibilità), dobbiamo notare che in questo esempio siamo in realtà particolarmente interessati alla errata classificazione di individui che effettivamente sono andati in default, mentre l’errata classificazione “buoni” è meno problematica. Fino ad ora, per assegnare una osservazioe alla classe di default, abbiamo usato una soglia del 50% per la probabilità a posteriori di default. Una possibilità per migliorare la sensibilità di questo classificatore è quella di abbassare la soglia. Per esempio, potremmo etichettare come “defaulter” qualunque cliente con una probabilità a posteriori di essere in default inferiore al 20%.Così facendo otterremo i seguenti risultati:

post <- predict(res)$posterior
threshold <- 0.2
default_hat_20 <- as.factor(ifelse(post[, 2] > threshold, 1, 0))
levels(default_hat_20) <- c("No", "Yes")
prop.table(table(default_hat_20, Default$default), margin = 2)

##               
## default_hat_20         No        Yes
##            No  0.97569049 0.41441441
##            Yes 0.02430951 0.58558559

confusionMatrix(data = default_hat_20, reference = Default$default,
                positive = "Yes")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction   No  Yes
##        No  9432  138
##        Yes  235  195
##                                           
##                Accuracy : 0.9627          
##                  95% CI : (0.9588, 0.9663)
##     No Information Rate : 0.9667          
##     P-Value [Acc > NIR] : 0.9869          
##                                           
##                   Kappa : 0.4921          
##                                           
##  Mcnemar's Test P-Value : 6.671e-07       
##                                           
##             Sensitivity : 0.5856          
##             Specificity : 0.9757          
##          Pos Pred Value : 0.4535          
##          Neg Pred Value : 0.9856          
##              Prevalence : 0.0333          
##          Detection Rate : 0.0195          
##    Detection Prevalence : 0.0430          
##       Balanced Accuracy : 0.7806          
##                                           
##        'Positive' Class : Yes             
##

dei 333 “defaulter”, ora LDA ne prvede correttamente tutti meno 138 (41.4%). Questo è un bel miglioramento! Tuttavia, questo miglioramento ha un suo prezzo: ora 235 individui “buoni” sono classificati in maniera errata. Come conseguenza, il tasso d’errore complessivo è leggermente aumentato passando al 3.73%. Questo potrebbe essere considerato un piccolo prezzo da pagare per una più accurata identificazione dei “defaulter”. La question chiave ora è come scegliere qual è il migliore valore di soglia. Sfortunatamente non ci sono risposte immediate, perché questa decisione si deve basare sulla conoscenza del fenomeno, per esempio sui costi associati al default.

Uno strumento popolare per determinare le performance di un classificatore è la “receiver operating characteristics curve”" (curva operativa caratteristica, o curva ROC). Questa è un grafico che mostra contemporaneamente i valori di sensibilità e specificità per tutti i possibili valori di soglia. In maniera più precisa, le curve ROC riportano sull’asse verticale il valore di sensibilità e sull’asse orizzontale 1 meno la corrispondente specificità, facendo variare la soglia su molti valori compresi tra 0 e 1. Le curve ROC sono utili per confrontare diveersi classificatori. Una sintesi delle performance complessive si un classificatore è data dall’indice AUC (Area Under the Curve: area sotto la curva): è l’area della superficie racchiusa tra la curva ROC e la bisettrice del primo quadrante. La curva ROC ideale dovrebbe “disegnare” un angolo superiore sinistro. Di conseguenza, più AUC è grande, migliore dovrebbe essere il classificatore.
Il valore più elevato possibile per AUC è 1. Il valore minimo, in linea di principio (ma non matematicamente), dovrebbe essere 0.
Esistono molti package R che includono funzioni per calcolare curve ROC. Uno dei più semplici da usare è il package pROC:

library(pROC)

roc(response = Default$default, predictor = post[, 2], auc = TRUE, ci = TRUE,
    plot = TRUE, main = "Curva ROC")

## Setting levels: control = No, case = Yes

## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Default$default, predictor = post[, 2],     auc = TRUE, ci = TRUE, plot = TRUE, main = "Curva ROC")
## 
## Data: post[, 2] in 9667 controls (Default$default No) < 333 cases (Default$default Yes).
## Area under the curve: 0.9496
## 95% CI: 0.9401-0.959 (DeLong)

Il valore di AUC per questo esempio è circa pari a 0.95, che è piuttosto prossimo al valore massimo ottenibile, per cui potrebbe essere considerato molto buono. Si noti che questa funzione una curva ROC con il valore di specificità sull’asse orizzontale, che quindi è inivertito. Per produrre una curva ROC standard con (1 - specificità) riportato sull’asse orizzontale, dobbiamo usare l’argomento legacy.axes = TRUE.

roc(response = Default$default, predictor = post[, 2], auc = TRUE, ci = TRUE,
    plot = TRUE, main = "Curva ROC", legacy.axes = TRUE)

## Setting levels: control = No, case = Yes

## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Default$default, predictor = post[, 2],     auc = TRUE, ci = TRUE, plot = TRUE, main = "Curva ROC", legacy.axes = TRUE)
## 
## Data: post[, 2] in 9667 controls (Default$default No) < 333 cases (Default$default Yes).
## Area under the curve: 0.9496
## 95% CI: 0.9401-0.959 (DeLong)

Per confrontare questi risultati con un altro classificatore, andiamo ad aggiungere alle variabili di previsione anche il reddito (income) dei clienti, che era stato escluso nell’analisi precedente:

res_new <- lda(default ~ ., data = Default)
res_new

## Call:
## lda(default ~ ., data = Default)
## 
## Prior probabilities of groups:
##     No    Yes 
## 0.9667 0.0333 
## 
## Group means:
##     studentYes   balance   income
## No   0.2914037  803.9438 33566.17
## Yes  0.3813814 1747.8217 32089.15
## 
## Coefficients of linear discriminants:
##                      LD1
## studentYes -1.746631e-01
## balance     2.243541e-03
## income      3.367310e-06

post_new <- predict(res_new)$posterior
# plot the ROC fot original model
roc(response = Default$default, predictor = post[, 2], auc = TRUE, ci = TRUE,
    plot = TRUE, col = "magenta", main = "Confronto curve ROC")

## Setting levels: control = No, case = Yes

## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Default$default, predictor = post[, 2],     auc = TRUE, ci = TRUE, plot = TRUE, col = "magenta", main = "Confronto curve ROC")
## 
## Data: post[, 2] in 9667 controls (Default$default No) < 333 cases (Default$default Yes).
## Area under the curve: 0.9496
## 95% CI: 0.9401-0.959 (DeLong)

# add the ROC fot new model
roc(response = Default$default, predictor = post_new[, 2], auc = TRUE,
    ci = TRUE, plot = TRUE, col = "cyan", add = TRUE)

## Setting levels: control = No, case = Yes
## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Default$default, predictor = post_new[,     2], auc = TRUE, ci = TRUE, plot = TRUE, col = "cyan", add = TRUE)
## 
## Data: post_new[, 2] in 9667 controls (Default$default No) < 333 cases (Default$default Yes).
## Area under the curve: 0.9495
## 95% CI: 0.9401-0.9589 (DeLong)

legend(x = "bottomright", legend = c("w/o income", "w income"),
       col = c("magenta", "cyan"), lty = rep(1, 2), lwd = rep(2, 2))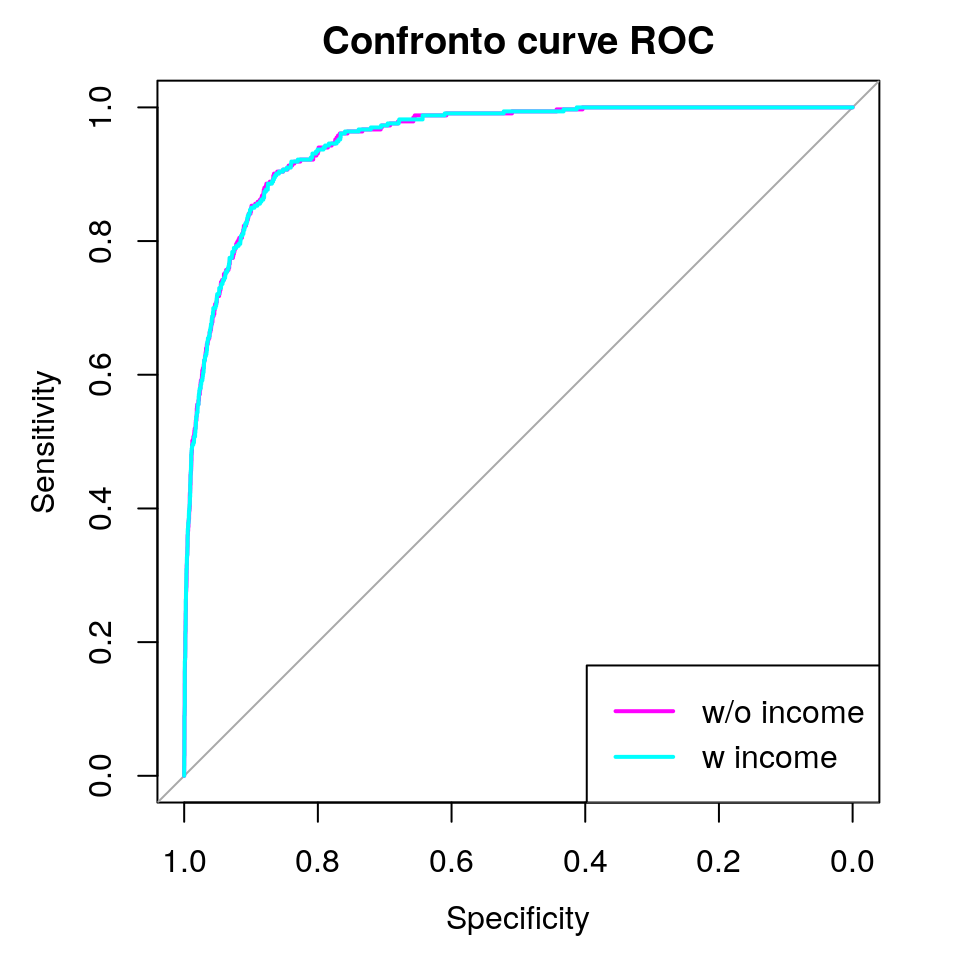

Le due curve ROC e i corrispondenti valori di AUC sono indistinguibili, pertanto sembra che l’aggiunta del reddito non aiuti nella discriminazione dei due gruppi. Potremmo eseguire altri confronti con altri modelli di classificazione, quali la regressione logistica stimata prima, che in questo esempio ritornerà sostanzialmente gli stessi risultati:

res_logit <- glm(default ~ student + balance, data = Default,
                 family = binomial(link = logit))
post_logit <- predict(res_logit, type = "response")
roc(response = Default$default, predictor = post[, 2], auc = TRUE, ci = TRUE,
    plot = TRUE, col = "magenta", main = "Confronto curve ROC")

## Setting levels: control = No, case = Yes

## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Default$default, predictor = post[, 2],     auc = TRUE, ci = TRUE, plot = TRUE, col = "magenta", main = "Confronto curve ROC")
## 
## Data: post[, 2] in 9667 controls (Default$default No) < 333 cases (Default$default Yes).
## Area under the curve: 0.9496
## 95% CI: 0.9401-0.959 (DeLong)

roc(response = Default$default, predictor = post_logit, auc = TRUE,
    ci = TRUE, plot = TRUE, col = "cyan", add = TRUE)

## Setting levels: control = No, case = Yes
## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Default$default, predictor = post_logit,     auc = TRUE, ci = TRUE, plot = TRUE, col = "cyan", add = TRUE)
## 
## Data: post_logit in 9667 controls (Default$default No) < 333 cases (Default$default Yes).
## Area under the curve: 0.9495
## 95% CI: 0.9401-0.959 (DeLong)

legend(x = "bottomright", legend = c("LDA", "logit"),
       col = c("magenta", "cyan"), lty = rep(1, 2), lwd = rep(2, 2))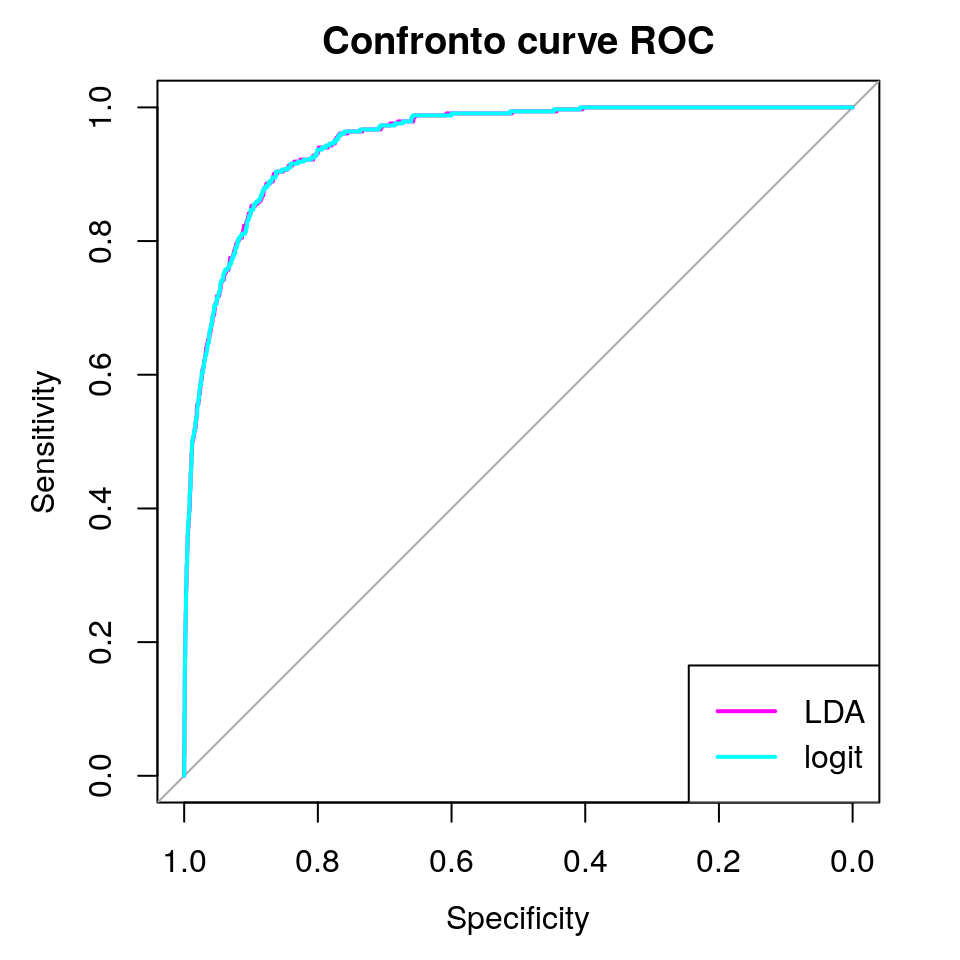

Una valutazione più appropriata della capacità predittiva di questi metodi dovrebbe coinvolgere il confronto dei tassi d’errore su un insieme di “test”. Questo insieme può essre ottenuto specificando l’argomento ‘subset’ nella funzione lda().

12.2 Un’Estensione: Analisi Discriminante Quadratica (QDA)

QDA rilassa l’assunto principale dell’LDA, assumendo che ogni classe abbia una sua matrice di (varianza/)covarianza. questa modifica produce limiti di decisione che in QDA diventano funzioni quadratiche dei predittori. Perché si dovrebbe preferire LDA o QDA? La risposta mette in gioco un trade-off tra distorsione e varianza dei predittori. In parole povere, LDA tende a produrre risultati migliori di QDA se ci sono relativamente poche osservazioni di training e quindi risulta cruciale ridurre la varianza. al contrario, QDA è raccomandata se l’insieme di dati di training (le osservazioni per costruire il predittore) è più ampio, e quindi la varianza del classificatore non è un problema importante.

La funzione qda() del package MASS esegue la QDA:

res_qda <- qda(default ~ student + balance, data = Default)
post_qda <- predict(res_qda)$posterior
threshold <- 0.2
default_qda <- as.factor(ifelse(post_qda[, 2] > threshold, 1, 0))
levels(default_qda) <- c("No", "Yes")
prop.table(table(default_qda, Default$default), margin = 2)

##            
## default_qda         No        Yes
##         No  0.96638047 0.35735736
##         Yes 0.03361953 0.64264264

confusionMatrix(data = default_qda, reference = Default$default,
                positive = "Yes")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction   No  Yes
##        No  9342  119
##        Yes  325  214
##                                           
##                Accuracy : 0.9556          
##                  95% CI : (0.9514, 0.9596)
##     No Information Rate : 0.9667          
##     P-Value [Acc > NIR] : 1               
##                                           
##                   Kappa : 0.469           
##                                           
##  Mcnemar's Test P-Value : <2e-16          
##                                           
##             Sensitivity : 0.6426          
##             Specificity : 0.9664          
##          Pos Pred Value : 0.3970          
##          Neg Pred Value : 0.9874          
##              Prevalence : 0.0333          
##          Detection Rate : 0.0214          
##    Detection Prevalence : 0.0539          
##       Balanced Accuracy : 0.8045          
##                                           
##        'Positive' Class : Yes             
##

roc(response = Default$default, predictor = post[, 2], auc = TRUE, ci = TRUE,
    plot = TRUE, col = "magenta", main = "Confronto curve ROC")

## Setting levels: control = No, case = Yes

## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Default$default, predictor = post[, 2],     auc = TRUE, ci = TRUE, plot = TRUE, col = "magenta", main = "Confronto curve ROC")
## 
## Data: post[, 2] in 9667 controls (Default$default No) < 333 cases (Default$default Yes).
## Area under the curve: 0.9496
## 95% CI: 0.9401-0.959 (DeLong)

roc(response = Default$default, predictor = post_qda[, 2], auc = TRUE,
    ci = TRUE, plot = TRUE, col = "cyan", add = TRUE)

## Setting levels: control = No, case = Yes
## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Default$default, predictor = post_qda[,     2], auc = TRUE, ci = TRUE, plot = TRUE, col = "cyan", add = TRUE)
## 
## Data: post_qda[, 2] in 9667 controls (Default$default No) < 333 cases (Default$default Yes).
## Area under the curve: 0.9495
## 95% CI: 0.9401-0.9589 (DeLong)

legend(x = "bottomright", legend = c("LDA", "QDA"),
       col = c("magenta", "cyan"), lty = rep(1, 2), lwd = rep(2, 2))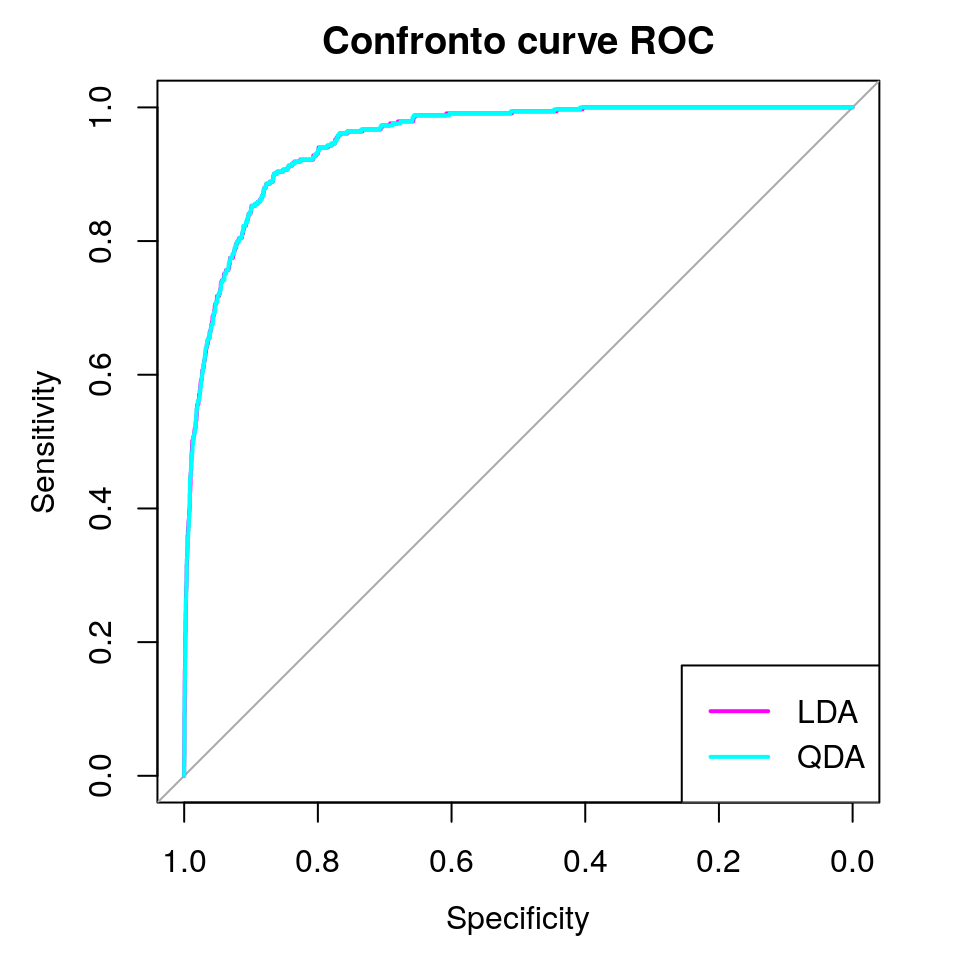

In questo esempio, QDA non sembra migliorare le performance di LDA, poiché entrambe le tecniche ritornano esattamente gli stessi risultati.

12.3 Esempio: Dati stock market

Consideriamo ora il dataset Smarket, un secondo dataset che contiene i guadagni percentuali per l’indice S&P 500 stock index su 1250 giorni, dall’inizio del 2001 fino alla fine del 2005. Per ogni giorno, sono riportati i guadagni percentuali per ciascuno di 5 giorni precedenti (da Lag1 a Lag5), il numero di azioni scambiate il giorno precedente (Volume, in miliardi), la percentuale di guadagno del giorno corrente (Today) e se il mercato è cresciuto o decresciuto in quel giorno (Direction):

library(GGally)

summary(Smarket)

##       Year           Lag1                Lag2                Lag3          
##  Min.   :2001   Min.   :-4.922000   Min.   :-4.922000   Min.   :-4.922000  
##  1st Qu.:2002   1st Qu.:-0.639500   1st Qu.:-0.639500   1st Qu.:-0.640000  
##  Median :2003   Median : 0.039000   Median : 0.039000   Median : 0.038500  
##  Mean   :2003   Mean   : 0.003834   Mean   : 0.003919   Mean   : 0.001716  
##  3rd Qu.:2004   3rd Qu.: 0.596750   3rd Qu.: 0.596750   3rd Qu.: 0.596750  
##  Max.   :2005   Max.   : 5.733000   Max.   : 5.733000   Max.   : 5.733000  
##       Lag4                Lag5              Volume           Today          
##  Min.   :-4.922000   Min.   :-4.92200   Min.   :0.3561   Min.   :-4.922000  
##  1st Qu.:-0.640000   1st Qu.:-0.64000   1st Qu.:1.2574   1st Qu.:-0.639500  
##  Median : 0.038500   Median : 0.03850   Median :1.4229   Median : 0.038500  
##  Mean   : 0.001636   Mean   : 0.00561   Mean   :1.4783   Mean   : 0.003138  
##  3rd Qu.: 0.596750   3rd Qu.: 0.59700   3rd Qu.:1.6417   3rd Qu.: 0.596750  
##  Max.   : 5.733000   Max.   : 5.73300   Max.   :3.1525   Max.   : 5.733000  
##  Direction 
##  Down:602  
##  Up  :648  
##            
##            
##            
##

ggpairs(Smarket)

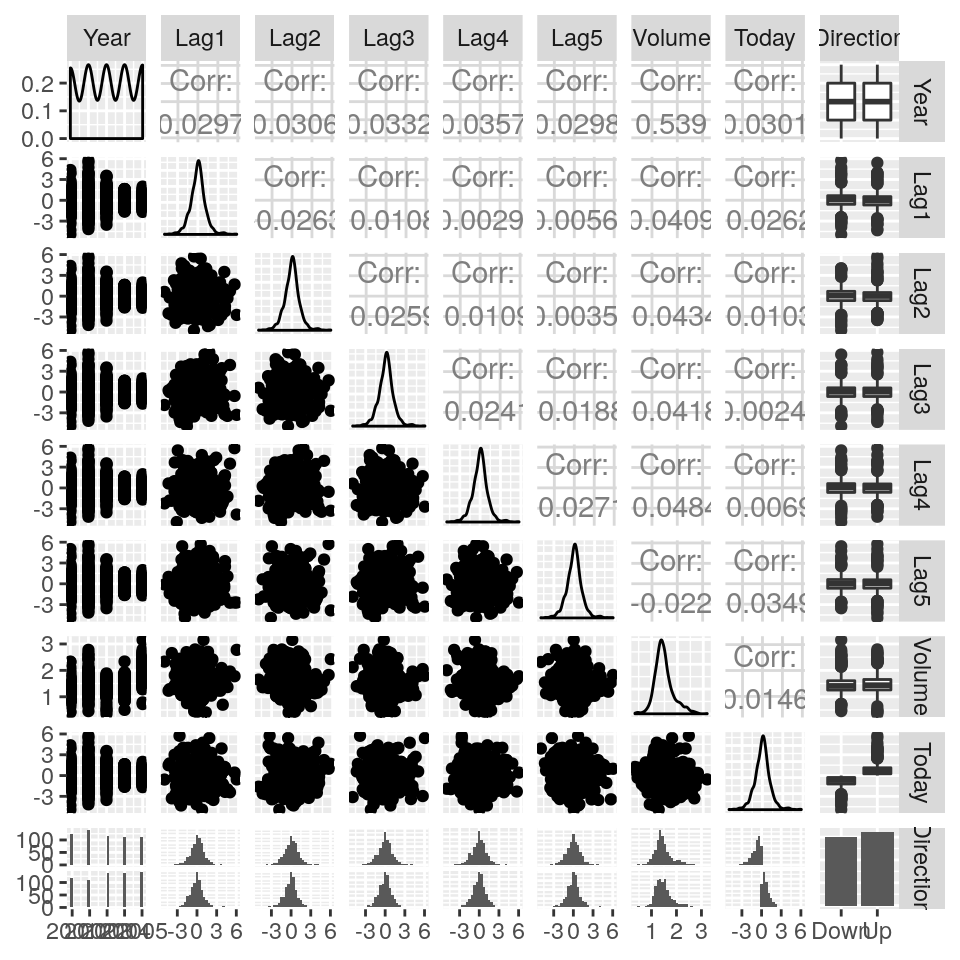
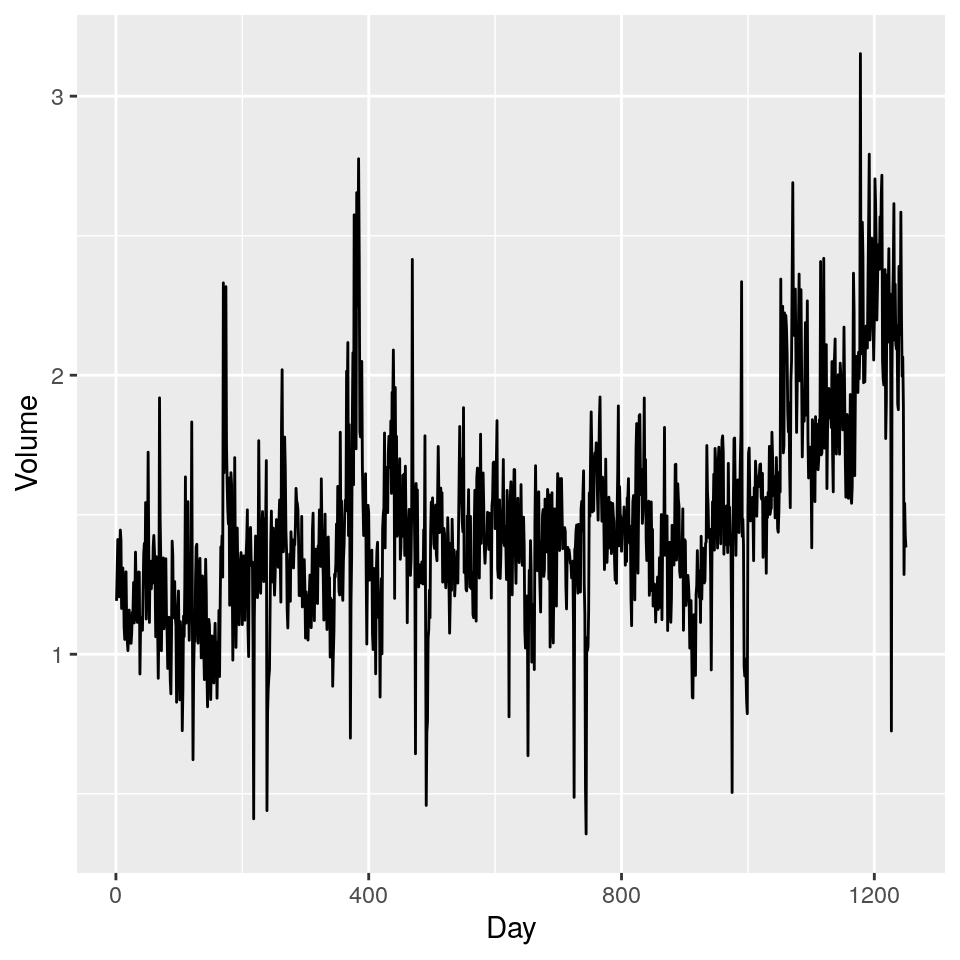
Le correlazioni tra le variabili dei giorni precedenti e quella corrente sono prossime a zero. La sola correlazione non trascurabile sembre essere quella tra Year e Volume, poiché il numero di azioni scambiate giornalmente è cresciuto dal 2001 al 2005:

ggp <- ggplot(Smarket, aes(x = 1:length(Volume), y = Volume)) +
  geom_line() +
    xlab("Day")
plot(ggp)

Vorremmo prevedere i valori di Direction usando le variabili da Lag1 a Lag5 e Volume. Con questo obiettivo, proveremo a confrontare i risultati della regressione logistica con LDA e QDA. Cominciamo dalla regressione logistica:

glm_fit <- glm(Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
               data = Smarket, family = binomial(link = logit))
summary(glm_fit)

## 
## Call:
## glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + 
##     Volume, family = binomial(link = logit), data = Smarket)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -1.446  -1.203   1.065   1.145   1.326  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.126000   0.240736  -0.523    0.601
## Lag1        -0.073074   0.050167  -1.457    0.145
## Lag2        -0.042301   0.050086  -0.845    0.398
## Lag3         0.011085   0.049939   0.222    0.824
## Lag4         0.009359   0.049974   0.187    0.851
## Lag5         0.010313   0.049511   0.208    0.835
## Volume       0.135441   0.158360   0.855    0.392
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1731.2  on 1249  degrees of freedom
## Residual deviance: 1727.6  on 1243  degrees of freedom
## AIC: 1741.6
## 
## Number of Fisher Scoring iterations: 3

glm_probs <- predict(glm_fit, type = "response")
glm_pred <- rep("Down", nrow(Smarket))
glm_pred[glm_probs > .5] <- "Up"
glm_pred <- as.factor(glm_pred)
confusionMatrix(data = glm_pred, reference = Smarket$Direction,
                positive = "Up")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction Down  Up
##       Down  145 141
##       Up    457 507
##                                           
##                Accuracy : 0.5216          
##                  95% CI : (0.4935, 0.5496)
##     No Information Rate : 0.5184          
##     P-Value [Acc > NIR] : 0.4216          
##                                           
##                   Kappa : 0.0237          
##                                           
##  Mcnemar's Test P-Value : <2e-16          
##                                           
##             Sensitivity : 0.7824          
##             Specificity : 0.2409          
##          Pos Pred Value : 0.5259          
##          Neg Pred Value : 0.5070          
##              Prevalence : 0.5184          
##          Detection Rate : 0.4056          
##    Detection Prevalence : 0.7712          
##       Balanced Accuracy : 0.5116          
##                                           
##        'Positive' Class : Up              
##

L’accuratezza sui dati di training è 52.2%, solo leggermente migliore della pura scelta casuale. Tuttavia, come già spiegato, il tasso d’errore di training è spesso ottimistico, poiché tende a sottostimare il tasso d’errore sui dati di test. Per otenere una migliore valutazione del modello di regressione logistico su questi dati, dovremmo adattare il modello usando solo parte dei dati, e quindi esaminare quanto bene il modello prevede i dati rimanenti dati (rimossi). Decidiamo quindi di usare le osservazioni dal 2001 al 2004 per il training e quelle dal 2005 per il test:

train <- (Smarket$Year < 2005)
Smarket_2005 <- Smarket[!train, ]
glm_fit <- glm(Direction ~Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
               data = Smarket, family = binomial(link = logit), subset = train)
glm_probs <- predict(glm_fit, Smarket_2005, type = "response")
glm_pred <- rep("Down", nrow(Smarket_2005))
glm_pred[glm_probs > .5] <- "Up"
glm_pred <- as.factor(glm_pred)
confusionMatrix(data = glm_pred, reference = Smarket_2005$Direction,
                positive = "Up")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction Down Up
##       Down   77 97
##       Up     34 44
##                                          
##                Accuracy : 0.4802         
##                  95% CI : (0.417, 0.5437)
##     No Information Rate : 0.5595         
##     P-Value [Acc > NIR] : 0.9952         
##                                          
##                   Kappa : 0.0054         
##                                          
##  Mcnemar's Test P-Value : 6.062e-08      
##                                          
##             Sensitivity : 0.3121         
##             Specificity : 0.6937         
##          Pos Pred Value : 0.5641         
##          Neg Pred Value : 0.4425         
##              Prevalence : 0.5595         
##          Detection Rate : 0.1746         
##    Detection Prevalence : 0.3095         
##       Balanced Accuracy : 0.5029         
##                                          
##        'Positive' Class : Up             
##

I tasso d’errore sui dati di test è 52%, peggio della semplice scelta casuale! Questo risultato non è poi così sorprendente, poiché è un fatto ben noto che non ci si debba generalmente aspettare di essere in grado di prevedere i guadagni dei giorni precedenti per prevedere le performance di mercato future. Proveremo a rimuovere i predittori con valori di p-value più elevati per cercare di migliorare il modello; useremo quindi il modello con le sole variabili Lag1 e Lag2:

glm_fit <- glm(Direction ~ Lag1 + Lag2, data = Smarket,
               family = binomial(link = logit), subset = train)
glm_probs <- predict(glm_fit, Smarket_2005, type = "response")
glm_pred <- rep("Down", nrow(Smarket_2005))
glm_pred[glm_probs > .5] <- "Up"
glm_pred <- as.factor(glm_pred)
confusionMatrix(data = glm_pred, reference = Smarket_2005$Direction,
                positive = "Up")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction Down  Up
##       Down   35  35
##       Up     76 106
##                                           
##                Accuracy : 0.5595          
##                  95% CI : (0.4959, 0.6218)
##     No Information Rate : 0.5595          
##     P-Value [Acc > NIR] : 0.5262856       
##                                           
##                   Kappa : 0.0698          
##                                           
##  Mcnemar's Test P-Value : 0.0001467       
##                                           
##             Sensitivity : 0.7518          
##             Specificity : 0.3153          
##          Pos Pred Value : 0.5824          
##          Neg Pred Value : 0.5000          
##              Prevalence : 0.5595          
##          Detection Rate : 0.4206          
##    Detection Prevalence : 0.7222          
##       Balanced Accuracy : 0.5335          
##                                           
##        'Positive' Class : Up              
##

Ora il 56% dei movimenti giornalieri è stato previsto correttamente.

Ora eseguiremo quindi una LDA usando solo le osservazioni prima del 2005:

lda_fit <- lda(Direction ~ Lag1 + Lag2, data = Smarket, subset = train)
lda_probs <- predict(lda_fit, Smarket_2005)$posterior[, 2]
lda_class <- predict(lda_fit, Smarket_2005)$class
confusionMatrix(data = lda_class, reference = Smarket_2005$Direction,
                positive = "Up")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction Down  Up
##       Down   35  35
##       Up     76 106
##                                           
##                Accuracy : 0.5595          
##                  95% CI : (0.4959, 0.6218)
##     No Information Rate : 0.5595          
##     P-Value [Acc > NIR] : 0.5262856       
##                                           
##                   Kappa : 0.0698          
##                                           
##  Mcnemar's Test P-Value : 0.0001467       
##                                           
##             Sensitivity : 0.7518          
##             Specificity : 0.3153          
##          Pos Pred Value : 0.5824          
##          Neg Pred Value : 0.5000          
##              Prevalence : 0.5595          
##          Detection Rate : 0.4206          
##    Detection Prevalence : 0.7222          
##       Balanced Accuracy : 0.5335          
##                                           
##        'Positive' Class : Up              
##

LDA fornisce praticamente gli stessi risultati della regressione logistica. Proviamo quindi con QDA:

qda_fit <- qda(Direction ~ Lag1 + Lag2, data = Smarket, subset = train)
qda_probs <- predict(qda_fit, Smarket_2005)$posterior[, 2]
qda_class <- predict(qda_fit, Smarket_2005)$class
confusionMatrix(data = qda_class, reference = Smarket_2005$Direction,
                positive = "Up")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction Down  Up
##       Down   30  20
##       Up     81 121
##                                           
##                Accuracy : 0.5992          
##                  95% CI : (0.5358, 0.6602)
##     No Information Rate : 0.5595          
##     P-Value [Acc > NIR] : 0.1138          
##                                           
##                   Kappa : 0.1364          
##                                           
##  Mcnemar's Test P-Value : 2.369e-09       
##                                           
##             Sensitivity : 0.8582          
##             Specificity : 0.2703          
##          Pos Pred Value : 0.5990          
##          Neg Pred Value : 0.6000          
##              Prevalence : 0.5595          
##          Detection Rate : 0.4802          
##    Detection Prevalence : 0.8016          
##       Balanced Accuracy : 0.5642          
##                                           
##        'Positive' Class : Up              
##

Questo indica che le previsioni tramite QDA sono accurate al più il 60% delle volte. Questo suggerisce che QDA può catturare la vera relazione in maniera leggermente più accurata di LDA e della regressione logistica. Ciò è confermato dal confronto delle curve ROC:

roc(response = Smarket_2005$Direction, predictor = glm_probs, auc = TRUE, ci = TRUE, plot = TRUE, col = "magenta", main = "Confronto curve ROC",
    legacy.axes = TRUE)

## Setting levels: control = Down, case = Up

## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Smarket_2005$Direction, predictor = glm_probs,     auc = TRUE, ci = TRUE, plot = TRUE, col = "magenta", main = "Confronto curve ROC",     legacy.axes = TRUE)
## 
## Data: glm_probs in 111 controls (Smarket_2005$Direction Down) < 141 cases (Smarket_2005$Direction Up).
## Area under the curve: 0.5584
## 95% CI: 0.4862-0.6307 (DeLong)

roc(response = Smarket_2005$Direction, predictor = lda_probs, auc = TRUE,
    ci = TRUE, plot = TRUE, col = "cyan", add = TRUE, legacy.axes = TRUE)

## Setting levels: control = Down, case = Up
## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Smarket_2005$Direction, predictor = lda_probs,     auc = TRUE, ci = TRUE, plot = TRUE, col = "cyan", add = TRUE,     legacy.axes = TRUE)
## 
## Data: lda_probs in 111 controls (Smarket_2005$Direction Down) < 141 cases (Smarket_2005$Direction Up).
## Area under the curve: 0.5584
## 95% CI: 0.4862-0.6307 (DeLong)

roc(response = Smarket_2005$Direction, predictor = qda_probs, auc = TRUE,
    ci = TRUE, plot = TRUE, col = "darkgray", add = TRUE, legacy.axes = TRUE)

## Setting levels: control = Down, case = Up
## Setting direction: controls < cases

## 
## Call:
## roc.default(response = Smarket_2005$Direction, predictor = qda_probs,     auc = TRUE, ci = TRUE, plot = TRUE, col = "darkgray", add = TRUE,     legacy.axes = TRUE)
## 
## Data: qda_probs in 111 controls (Smarket_2005$Direction Down) < 141 cases (Smarket_2005$Direction Up).
## Area under the curve: 0.562
## 95% CI: 0.4897-0.6343 (DeLong)

legend(x = "bottomright", legend = c("Regressione logistica", "LDA", "QDA"),
       col = c("magenta", "cyan", "darkgray"), lty = rep(1, 3),
       lwd = rep(2, 3))

12.4 Alcuni cenni di teoria

Due sono gli approcci principali all’Analisi Discriminante:

Il primo ha preso origine da Fisher, che ha sviluppato il metodo delle Funzioni Discriminanti Lineari (Linear Discriminant Functions), senza formulare alcun assunto distributivo sui dati (ad esclusione della matrice di varianze/covarianze costanti all’interno dei gruppi)
Il secondo,invece, assume che la distribuzione dei dati segue un modello normale multivariato, e fondamentalmente applica metodi di rapporto di verosimiglianza (LR) per eseguire la classificazione

12.4.1 Funzioni Discriminanti Lineari

Supponiamo, per semplicità, che due gruppi di ossrvazioni debbano essere discriminati sulla base delle loro misurazioni su due dimensioni. Abbiamo quindi \(g=2\) gruppi di ossrvazioni; per ciascun gruppo abbiamo \(n\) osservazioni su \(p=2\) dimensioni (continue, sempre per semplicità).
Una possibile rappresentazione dei punti su uno spazio cartesiano bidimensionale potrebbe essere il seguente:

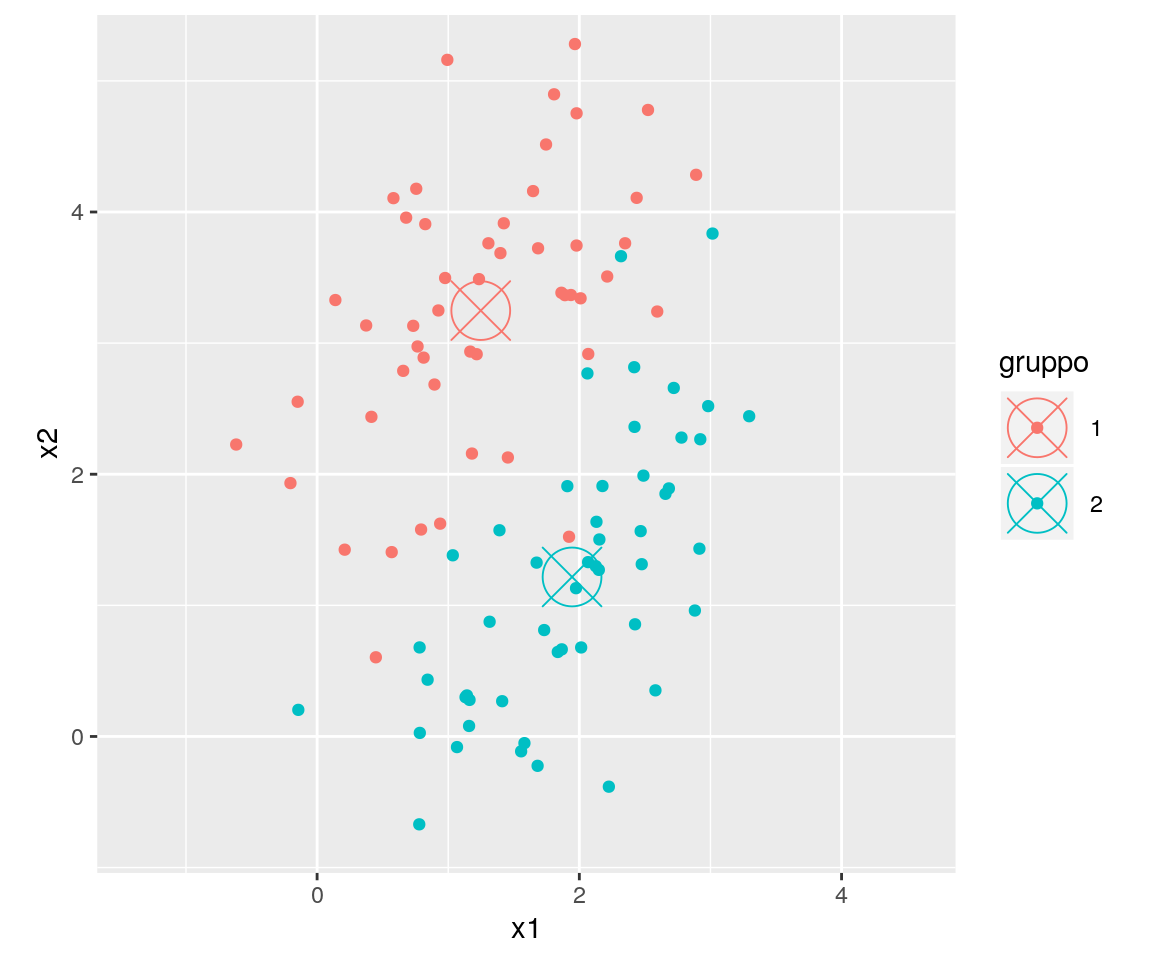
Nel grafico qui sopra i punti rappresentano le singole osservazioni e i colori i gruppi di appartenenza. Le medie dei due sottogruppi sono evidenziate dai cerchi con le “X”.

Ora vogliamo trovare una proiezione lineare dei dati su una sola dimensione (in questo caso), tale per cui i due gruppi di osservazioni su questa nuova dimensione siano “massimamente separati”.
Questo problema si risolve cercando la soluzione di: \[ \begin{matrix} \max\\ \underline{a} \end{matrix}\left\{\frac{\left [ \underline{a}^T \left(\underline{\overline{x}}_1-\underline{\overline{x}}_2 \right) \right ]}{\underline{a}^T S \underline{a}}\right\} \] Dove \(S\) è la matrice di varianza/covarianza interna ai sottogruppi aggregata, \(\underline{a}\) è il vettore dei pesi (da individuare) che ci genera la trasformazione lineare, e \(\underline{\overline{x}}_1\) e \(\underline{\overline{x}}_2\) sono, rispettivamente, il vettore bivariato delle medie per il primo e per il secondo gruppo.

Per fortuna la soluzione del problema indicato qui sopra esiste ed è data da:

\[ \underline{a} = S^{-1} \left(\underline{\overline{x}}_1-\underline{\overline{x}}_2 \right) \] e quindi \[ z=\underline{a}^T \underline{x} = \left(\underline{\overline{x}}_1-\underline{\overline{x}}_2 \right)^T S^{-1} \underline{x} \]

Dove \(\underline{x}\) è un generico vettore dei dati osservati (“riga” della matrice delle osservazioni), \(\underline{a}^T \underline{x}\) è la cosiddetta Funzione Discriminante Lineare di Fisher e \(z\) è il valore della proiezione per la generica osservazione multivariata \(\underline{x}\) che dovebbe permettere di discriminare l’appartenenza ad un gruppo rispetto all’altro.

Il grafico che segue illustra l’operazione della proiezione dei punti sulla nuova dimensione, o componente discriminante.

Qui sopra: la linea nera rappresenta la dimensione su cui sono proiettati i punti, le proiezioni sulla linea sono indicate dalle linee tratteggiate ed i punti proiettati sono indicati con il simbolo “+”.
Notate come le proiezioni dei punti sulla linea nera non siano per forza perpendicolari, e ciò perché la proiezione è fatta in maniera tale da massimizzare la distinzione tra gruppi sulla linea nera stessa.

Il grafico che segue, invece, “posiziona” (senza mostrarla) la linea nera del grafico precedente sull’asse delle ascisse e segna su questo asse i singoli punti proiettati (le barrette verticali); dopo ciò, mostra la densità di probabilità osservata per i due gruppi, con colori diversi.

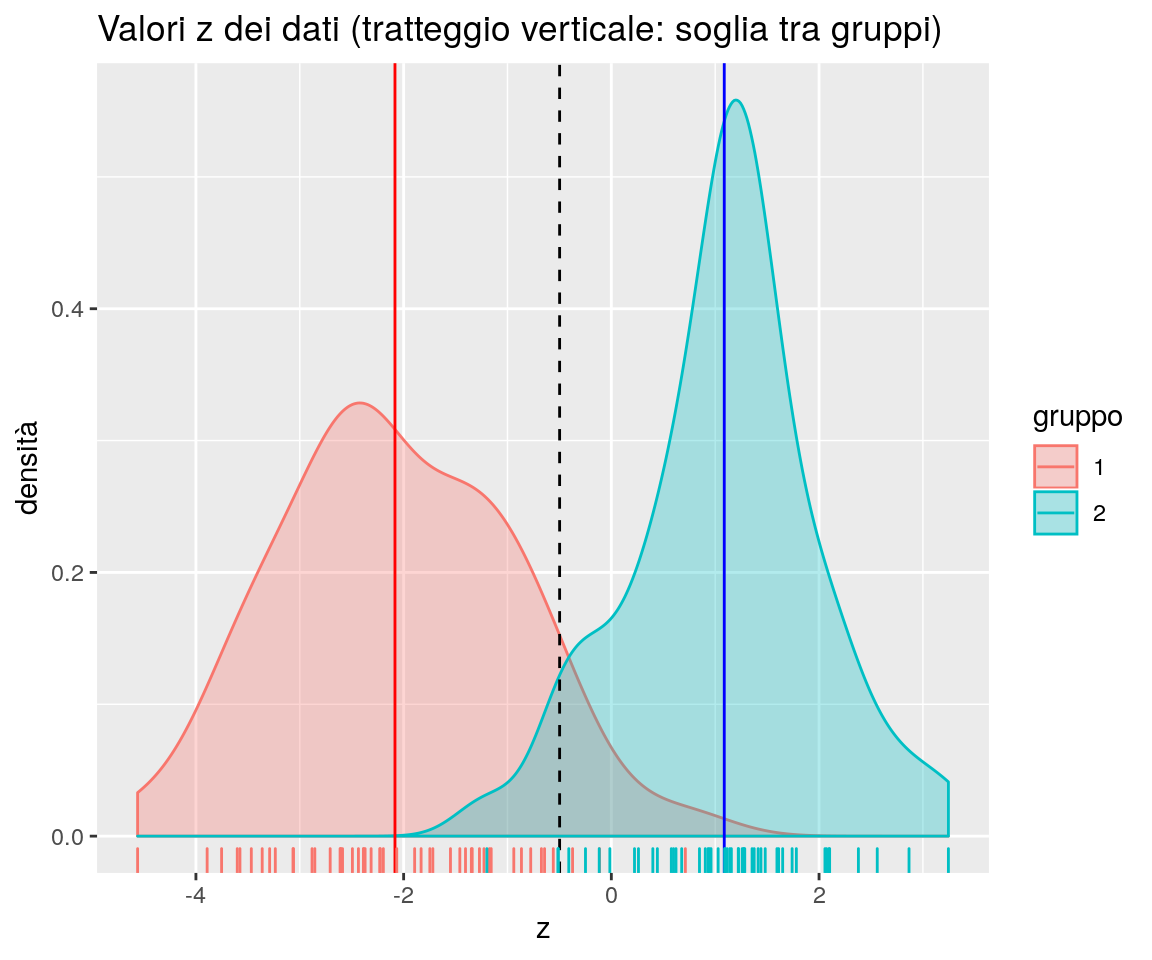
La soglia di discriminazione tra i gruppi (la linea nera tratteggiata nel grafico qui sopra) è usualmente data dal valore intermedio dei punteggi delle medie dei due gruppi, e quindi il criterio per assegnare una generica osservazione \(\underline{x}_0\) al primo gruppo sarà: \[ \left(\underline{\overline{x}}_1-\underline{\overline{x}}_2 \right)^T S^{-1} \underline{x}_0 - \left(\underline{\overline{x}}_1-\underline{\overline{x}}_2 \right)^T S^{-1} \left(\frac{\underline{\overline{x}}_1+\underline{\overline{x}}_2}{2} \right) >0 \]

Qualora il numero di gruppi da discriminare \(g\) fosse maggiore di 2, possiamo applicare una generalizzazione del metodo indicato qui sopra, che è più complessa da esprimere, e che richiede la massimizzazione, rispetto ad \(\underline{a}\), della funzione: \[ R = \frac{\underline{a}^T B \underline{a}}{\underline{a}^T W \underline{a}} \] Sotto alcuni vincoli sui valori di \(\underline{a}\) e \(\underline{a}^T \underline{x}\).
Nella formula qui sopra, \(B\) è una stima della matrice di varianza/covarianza “tra gruppi”, e \(W\) è una stima della matrice di varianza/covarianza “entro gruppi” (che, ricordiamo, è ipotizzata costante all’interno dei gruppi).
Nel caso generale, si ottengono \(max\{p,g-1\}\) funzioni discriminanti lineari ortogonali.

12.4.2 Modelli Probabilistici

Un approccio alternativo alla discriminazione è tramite modelli probabilistici.
Supponiamo di avere i valori \(\pi_i (i=1, \cdots, g)\), che indicano le probabilità a priori che una specifica osservazione appartenga al gruppo \(i\)-mo, e indichiamo con \(p(\underline{x}|i)\) le densità delle distribuzioni delle osservazioni delle variabili esplicative per ciascun gruppo. Allora la probabilità a posteriori di appartenere al gruppo \(i\)-mo dopo aver osservato \(\underline{x}\) è: \[ p(i|\underline{x}) = \frac{\pi_i p(\underline{x} | i)}{p(\underline{x})} \propto \pi_i p(\underline{x} | i) \] ed è relativamente semplice dimostrare che la regola di allocazione che produce il numero atteso di errori più piccolo è quella che sceglie la classe con valore massimo di \(p(i | \underline{x})\) (regola di Bayes).

Ora, se supponiamo che la distribuzione delle osservazioni per il gruppo \(i\) sia una legge normale multivariata con media \(\mu_i\) e matrice di covarianza \(\Sigma_i\) . Allora la regola di Bayes minimizza \[ Q_i = −2 \log(p(\underline{x} | i)) − 2 \log(\pi_i) = (\underline{x} − \mu_i )^T\Sigma_i^{−1} (\underline{x} − \mu_i ) + \log(|\Sigma_i |) − 2 \log( \pi_i) \]

Il primo addendo dell’ultimo termine della formula è la distanza di Mahalanobis al quadrato dal centro di gruppo. La regola di assegnare l’osservazione al gruppo \(i\) che minimizzala formula qui sopra produce la Funzione Discrimiante Quadratica.

Supponiamo ora che i gruppi abbiamo una matrice di covarianze costante \(\Sigma\). Le differenze in \(Q_i\) diventano quindi funzioni lineari di \(\underline{x}\), e possiamo massimizzare \(−Q_i /2\) o \[ L_i = \underline{x} \Sigma^{−1} \mu^T_i − \mu_i Σ^{−1} \mu^T_i /2 + \log(\pi_i) \] Se sostituiamo \(\mu_i\) e \(\Sigma\) con le stime campionarie (media campionaria \(\overline{\underline{x}}\) e matrice di varianze/covarianze campionaria \(S\)), allora la formula qui sopra fornisce risultati che, per \(\pi_i=1/g\), sono equivalenti a quelli delle funzioni discriminanti lineari.