Capitolo 9 Introduzione all’algoritmo DBSCAN
9.1 Introduzione
Il DBSCAN (Density-Based Spatial Clustering of Applications with Noise) è un metodo di clustering proposto nel 1996 da Martin Ester, Hans-Peter Kriegel, Jörg Sander and Xiaowei Xu. È basato sulla densità perché connette regioni di punti con densità sufficientemente alta. DBSCAN è un algoritmo di clustering tra i più usati ed è anche il più citato nella letteratura scientifica.
DBSCAN stima la densità attorno a ciascun punto (item) contando il numero di punti in un intorno \(\varepsilon\) (o \(eps\)) specificato dall’utente, ed applica delle soglie chiamate \(minPts\) per identificare i punti “core”, “border” e “noise”. In un secondo passaggio, i punti core sono riuniti in un cluster, se sono “density-reachable” (“raggiungibili per densità”, cioè se esiste una catena di punti core in cui ogni punto ricade all’interno dell’eps-intorno del successivo). Infine i punti di bordo sono assegnati ai cluster. L’algoritmo richiede solo i parametri \(eps\) e \(minPts\).
Consideriamo quindi un insieme di punti da raggruppare all’interno di un qualche spazio. Per gli obiettivi del clustering DBSCAN, i punti (item) sono classificati come “core point”, (density-)reachable o outlier, in base alle seguenti regole:
- Un punto \(p\) è un punto core se almeno \(minPts\) punti sono entro la distanza \(\varepsilon\) (\(\varepsilon\) abbiamo detto che è il raggio massimo per il vicinato di \(p\)) da esso (incluso \(p\) stesso). Questi punti sono detti “direttamente raggiungibili” da \(p\).
- Un punto \(q\) è direttamente raggiungibile da \(p\) se il punto \(q\) è entro la distanza \(\varepsilon\) dal punto \(p\), con \(p\) che deve essere un core point.
- Un punto \(q\) è raggiungibile da \(p\) se esiste un percorso \(p_1, \dots , p_n\) con \(p_1 = p\) e \(p_n = q\), dove ogni \(p_{i+1}\) è direttamente raggiungibile da \(p_i\) (tutti i punti nel percorso devono essere core, con la sola possibile eccezione di \(q\)).
- Tutti i punti non raggiungibili da altri punti sono outlier.
Ora, se \(p\) è un core point, allora questo forma un cluster insieme a tutti gli altri punti (core o non-core) che sono raggiungibili da esso. Ogni cluster contiene almeno un punto core; punti non-core possono essere parte di un cluster, ma ne formano il “bordo” (“edge”), poiché non possono essere usati per raggiungere altri punti.
(By Chire - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17045963)
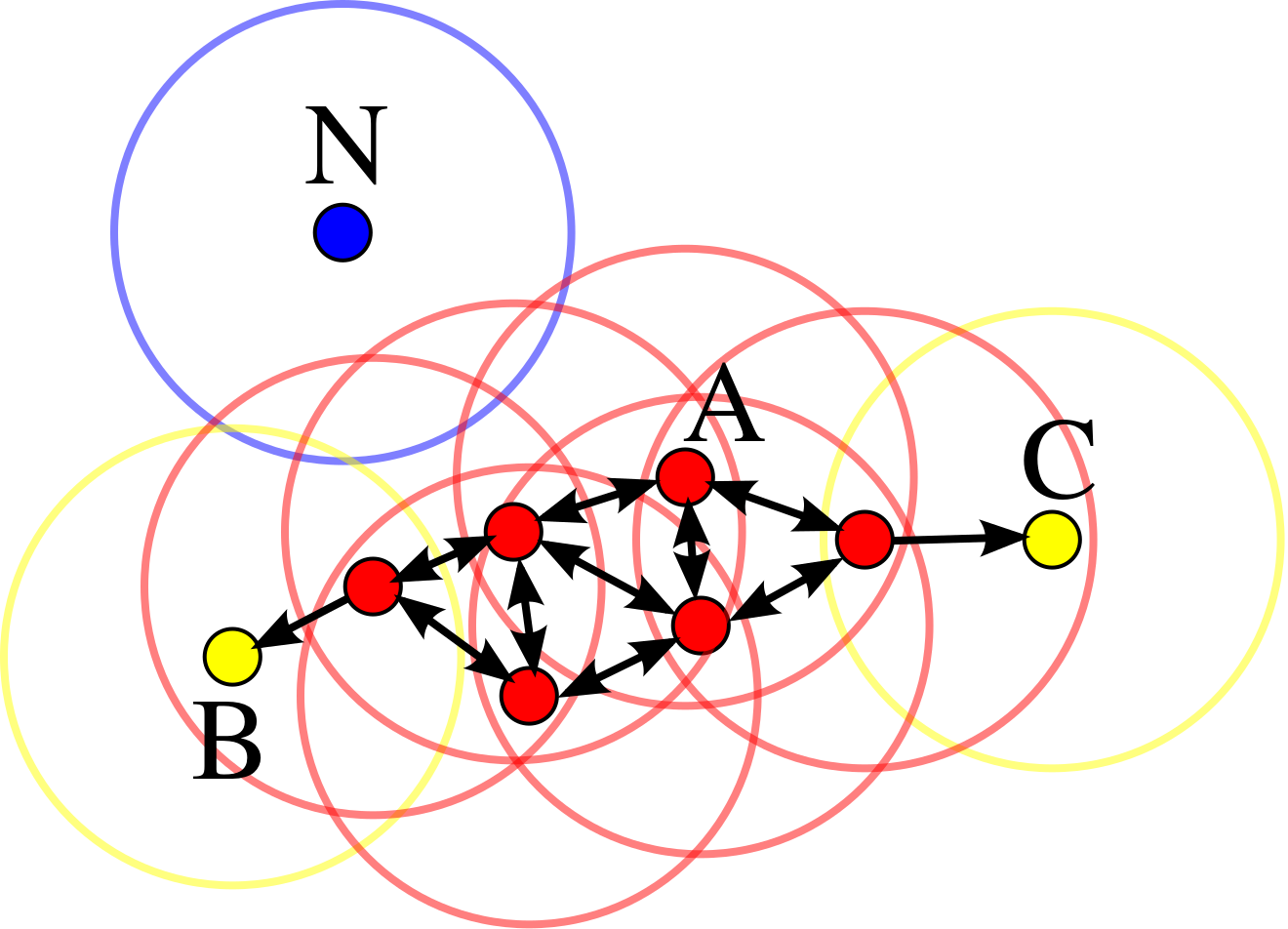
Nel diagramma qui sopra, \(minPts = 4\). Il punto \(A\) e gli altri punti rossi sono punti core, poiché l’area che circonda questi punti in un raggio di ampiezza \(\varepsilon\) contiene almeno 4 punti (incluso il punto stesso). Poiché i punti rossi sono tutti raggiunibili tra di loro, questi formano un singolo cluster. I punti \(B\) e \(C\) non sono punti core, ma sono raggiungibili da \(A\) (attraverso altri punti core) e quindi appartengono a loro volta al cluster. Il punto \(N\) è un punto di rumore (noise) poiché non è un punto core e non è nemmeno un punto direttamente raggiungibile.
La raggiungibilità non è una relazione simmetrica poiché, per definizione, un punto non può essere raggiungibile da un punto non-core, indipendentemente dalla distanza (quindi un punto non-core può essere raggiungibile, ma nulla può essere raggiunto da esso). Pertanto, è necessaria un’ulteriore nozione di connessione per definire formalmente l’estensione dei cluster trovati da DBSCAN. Due punti \(p\) e \(q\) sono “density-connected” se esiste un punto \(o\) tale che sia \(p\) che \(q\) siano raggiungibili da \(o\). La density-connectedness è simmetrica.
Un cluster quindi soddisfa due proprietà:
- Tutti i punti del cluster sono mutuamente density-connected.
- Se un punto è density-raggiungibile da un qualunque punto del cluster, allora è parte del cluster stesso.
9.1.1 Algoritmo in astratto
L’algoritmo DBSCAN può essere esemplificato con i seguenti passaggi:
- Trova gli \(\varepsilon\)-vicini (eps-vicini) di ciascun punto, ed identifica i punti core con più di \(minPts\) vicini.
- Trova i componenti connessi dei punti core nel grafico dei vicini, ignorando tutti i punti non-core.
- Assegna ciascun punto non-core ad un cluster vicino se il cluster è un \(\varepsilon\) (\(eps\)) vicino, altrimenti assegnalo al rumore.
9.2 Esempio: dati iris
Questo esempio è tratto dall’help della funzione dbscan() dell’omonimo package. Carichiamo innnanzitutto il package dbscan:
Prendiamo i dati iris, teniamo solo le colonne delle misurazioni numeriche, trasformandolo poi in matrice:
Ora troviamo il parametro eps usando un grafico k-NN per k = dimensioni del dataset + 1.
Il grafico mostra, per ogni punto ordinato rispetto alla distanza dai suoi k vicini, ed individuato dalla posizione d’ordine sull’asse delle ordinate, il valore di distanza stessa sull’asse delle ordinate.
Il punto di gomito sulla linea così tracciata può essere considerato il valore da utilizzare per eps:
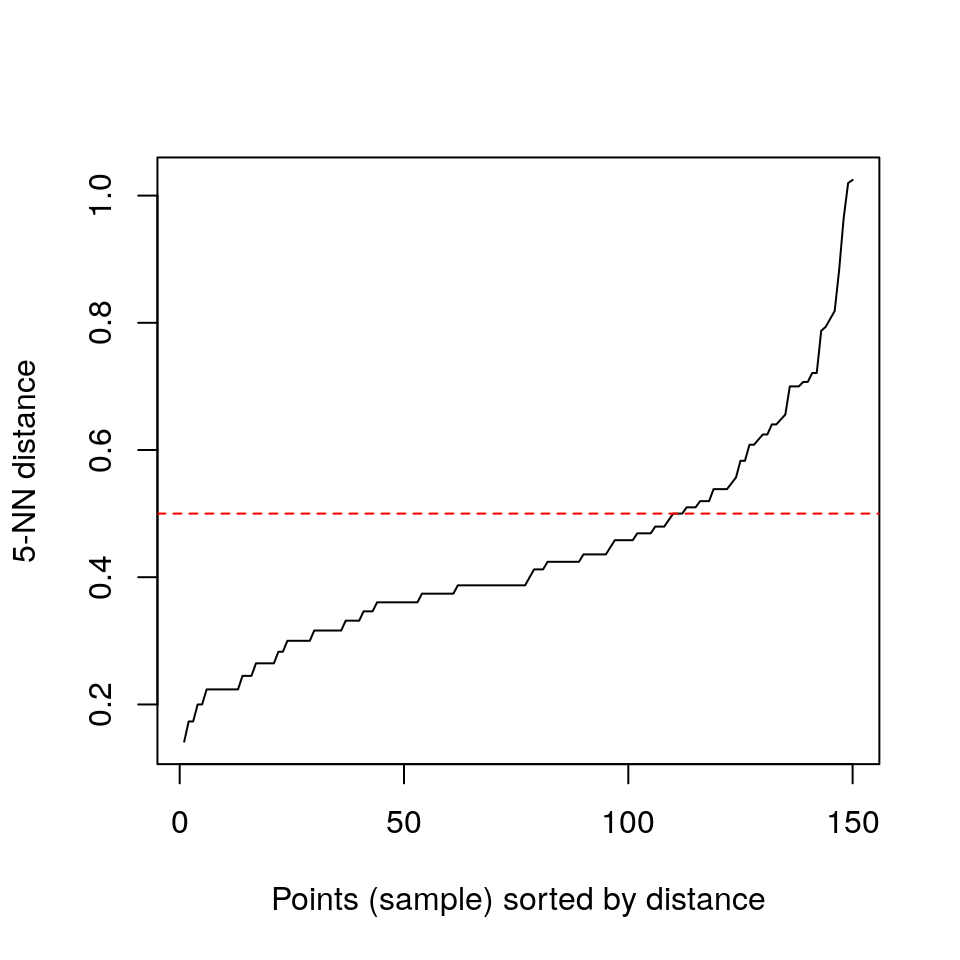
Eseguiamo il clustering con eps=0.5 (punto di gomito del grafico qui sopra) e minPts = 5 (numero dimensioni + 1: la regola di massima per questi problemi di classificazione)
## DBSCAN clustering for 150 objects.
## Parameters: eps = 0.5, minPts = 5
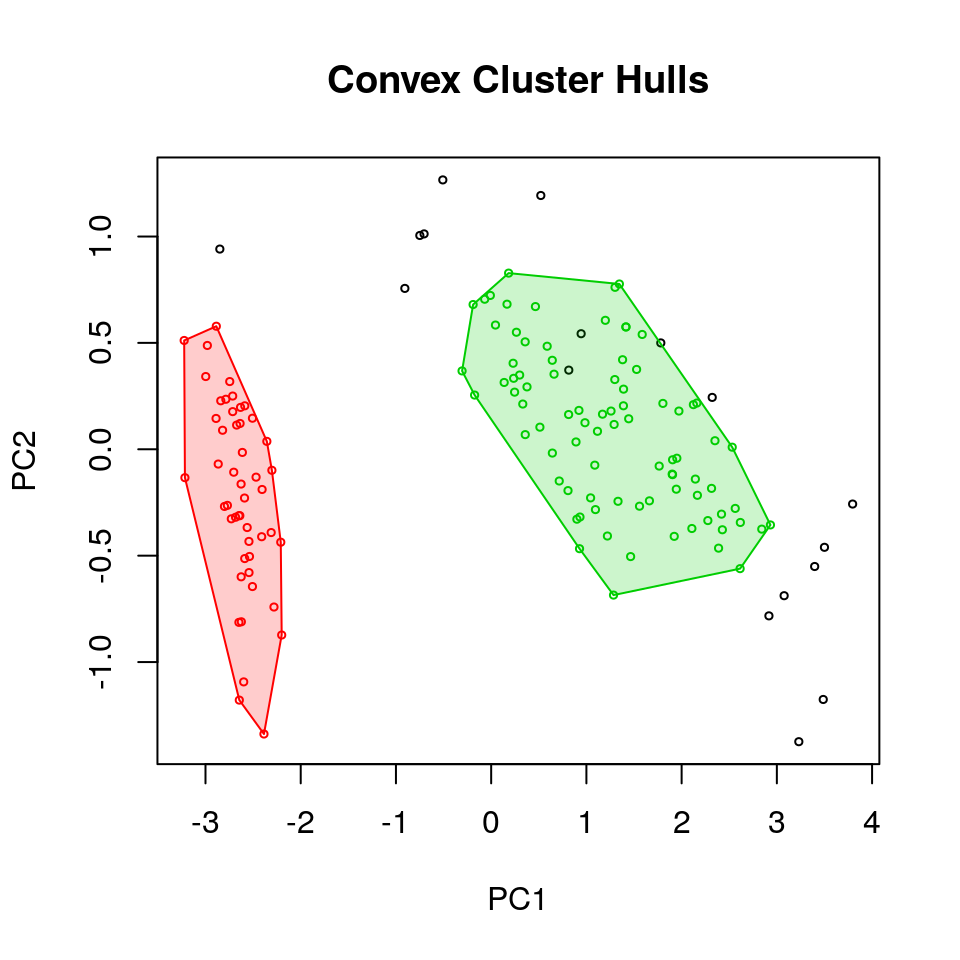
## The clustering contains 2 cluster(s) and 17 noise points.
##
## 0 1 2
## 17 49 84
##
## Available fields: cluster, eps, minPts
Il grafico che segue illustra i raggruppamenti così creati, con i gruppi evidenziati tramite aree convesse colorate.
Si noti che non sono tracciate le variabili originarie, ma le prime due componenti principali calcolate sulle misurazioni: