Capitolo 19 Variazioni sul Modello Lineare (LM)

19.1 Introduzione

Precederemo ora a confrontare i risultati conseguenti all’uso di tecniche di fitting diverse per un modello lineare. Faremo questo usando dati simulati con molte variabili indipendenti, la prima delle quali altamente correlata con alcune delle altre:

# Genera dati simulati
set.seed(10)
n <- 1000
p <- 100
X <- data.frame(matrix(runif(n*p), nrow = n, ncol = p))
# Da un nome alle colonne dei dati
names(X) <- paste("x", 1:ncol(X), sep = "")
# La prima colonna è molto correlata con le colonne dalla 2 alla 5.
X$x1 <- X$x2 + 2*X$x3 + 3*X$x4 - 4*X$x5 + rnorm(n, sd = .0001)
# Il modello per la variabile dipendente
X$y <- 4 + 0.2*X$x1 + .5*X$x2 - .9*X$x3 + X$x4 - 0.5*X$x5 + 0.2*X$x6 + rnorm(n, mean = 0, sd = 1)

dt <- X
rm(X)

Poiché nel data frame qui sopra solo le colonne dalla 1 alla 6 e la 101 sono tra loro nella realtà correlate, una matrice di scatterplot di queste colonne (insieme con poche altre colonne) può essere utile per
mostrare le relazioni tra queste variabili:

library(ggplot2)
library(GGally)

ggpairs(data = dt, columns = c(1:10,101), mapping = aes(alpha = 0.3))

Facciamo anche qualche test sulla collinearità:

# Test di collinearità
X <- as.matrix(dt[,1:10])
library(Matrix)
rankMatrix(X)

## [1] 10
## attr(,"method")
## [1] "tolNorm2"
## attr(,"useGrad")
## [1] FALSE
## attr(,"tol")
## [1] 2.220446e-13

try(solve(t(X)%*%X))

##                x1            x2            x3            x4            x5
## x1   9.968180e+04 -9.968229e+04 -1.993639e+05 -2.990448e+05  3.987275e+05
## x2  -9.968229e+04  9.968279e+04  1.993649e+05  2.990463e+05 -3.987294e+05
## x3  -1.993639e+05  1.993649e+05  3.987284e+05  5.980905e+05 -7.974560e+05
## x4  -2.990448e+05  2.990463e+05  5.980905e+05  8.971328e+05 -1.196180e+06
## x5   3.987275e+05 -3.987294e+05 -7.974560e+05 -1.196180e+06  1.594911e+06
## x6   9.354702e-01 -9.369787e-01 -1.872229e+00 -2.807539e+00  3.740330e+00
## x7  -1.189115e-01  1.180787e-01  2.368966e-01  3.554463e-01 -4.773766e-01
## x8  -4.510523e-01  4.503798e-01  9.002870e-01  1.351933e+00 -1.805298e+00
## x9  -9.756490e-01  9.746218e-01  1.950252e+00  2.925766e+00 -3.903910e+00
## x10  1.202462e+00 -1.203997e+00 -2.406063e+00 -3.608626e+00  4.809310e+00
##               x6           x7           x8           x9          x10
## x1   0.935470215 -0.118911528 -0.451052346 -0.975648985  1.202462488
## x2  -0.936978671  0.118078721  0.450379809  0.974621756 -1.203996720
## x3  -1.872229008  0.236896550  0.900286952  1.950252112 -2.406062508
## x4  -2.807539247  0.355446317  1.351932662  2.925765710 -3.608625756
## x5   3.740329831 -0.477376627 -1.805298142 -3.903909576  4.809309718
## x6   0.011075231 -0.001325552 -0.001895663 -0.001065308 -0.001121372
## x7  -0.001325552  0.010275857 -0.001575933 -0.000953953 -0.001463833
## x8  -0.001895663 -0.001575933  0.010999641 -0.000911617 -0.001275055
## x9  -0.001065308 -0.000953953 -0.000911617  0.010208522 -0.002058651
## x10 -0.001121372 -0.001463833 -0.001275055 -0.002058651  0.010928909

Notate che la matrice $(\underline{X}^T \underline{X})^{-1}$ ha valori molto elevati sulla diagonale. Ciò è conseguenza della collinearità tra i predittori. Questo inoltre produrrà probabilmente errori standard molto alti e stime dei parametri molto instabili (poiché la matrice di varianza/covarianza delle stime dei parametri è uguale a $\sigma^2 (\underline{X}^T \underline{X})^{-1}$).

Per valutare le performance predittive relative dei metodi che studieremo, spezziamo il dataset in due insiemi, di training (75%) e di test (25%):

# Divide i dati in data frame di training e data frame di test
sel_train <- sample(1:nrow(dt), replace = FALSE, size = n*.75)
dt_train <- dt[sel_train, ]
dt_test <- dt[setdiff(1:n, sel_train), ]

19.2 Minimi Quadrati Ordinari (OLS)

Questa tecnica usualmente non ottiene risultati eccezionali per modelli in cui siano presenti tante variabili indipendenti e solo alcune di queste siano effettivamente collegate alla variabile dipendente; i minimi quadrati ordinari spesso non hanno buone performance anche nel caso in cui ci sia una elevata collinearità (quando una variabile indipendente è fortemente correlata con una o più delle altre variabili indipendenti) tra i predittori:

ols_fit <- lm(y ~ ., data = dt_train)
summary(ols_fit)

## 
## Call:
## lm(formula = y ~ ., data = dt_train)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.86662 -0.59634 -0.03644  0.59663  2.82037 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.404e+00  6.705e-01   6.568 1.05e-10 ***
## x1           2.881e+02  3.774e+02   0.763  0.44558    
## x2          -2.873e+02  3.774e+02  -0.761  0.44677    
## x3          -5.767e+02  7.548e+02  -0.764  0.44516    
## x4          -8.628e+02  1.132e+03  -0.762  0.44631    
## x5           1.151e+03  1.510e+03   0.762  0.44621    
## x6           3.247e-01  1.332e-01   2.437  0.01506 *  
## x7           6.211e-02  1.302e-01   0.477  0.63353    
## x8          -1.945e-01  1.333e-01  -1.459  0.14492    
## x9          -5.208e-02  1.311e-01  -0.397  0.69118    
## x10         -3.371e-02  1.319e-01  -0.256  0.79832    
## x11         -4.370e-02  1.305e-01  -0.335  0.73784    
## x12         -1.770e-01  1.323e-01  -1.338  0.18149    
## x13          2.674e-01  1.370e-01   1.952  0.05137 .  
## x14          6.130e-02  1.326e-01   0.462  0.64392    
## x15          1.961e-01  1.348e-01   1.455  0.14615    
## x16          1.658e-01  1.279e-01   1.296  0.19534    
## x17          1.293e-01  1.341e-01   0.965  0.33513    
## x18          3.966e-03  1.345e-01   0.029  0.97649    
## x19         -1.949e-03  1.342e-01  -0.015  0.98842    
## x20         -4.913e-02  1.343e-01  -0.366  0.71464    
## x21          2.219e-02  1.334e-01   0.166  0.86800    
## x22          1.878e-02  1.321e-01   0.142  0.88694    
## x23          8.421e-02  1.333e-01   0.632  0.52772    
## x24         -2.245e-03  1.347e-01  -0.017  0.98671    
## x25          5.547e-02  1.380e-01   0.402  0.68786    
## x26         -2.142e-01  1.340e-01  -1.599  0.11033    
## x27          8.894e-02  1.359e-01   0.655  0.51300    
## x28         -1.250e-01  1.354e-01  -0.923  0.35619    
## x29         -3.115e-01  1.370e-01  -2.273  0.02334 *  
## x30         -6.000e-02  1.366e-01  -0.439  0.66070    
## x31         -2.529e-03  1.277e-01  -0.020  0.98421    
## x32          3.637e-01  1.317e-01   2.760  0.00594 ** 
## x33         -1.028e-01  1.334e-01  -0.770  0.44135    
## x34          4.451e-01  1.364e-01   3.262  0.00116 ** 
## x35          1.966e-02  1.301e-01   0.151  0.87993    
## x36         -2.162e-02  1.303e-01  -0.166  0.86829    
## x37         -1.130e-01  1.293e-01  -0.874  0.38262    
## x38         -1.510e-01  1.331e-01  -1.134  0.25713    
## x39          3.629e-03  1.325e-01   0.027  0.97816    
## x40          1.417e-01  1.345e-01   1.053  0.29260    
## x41         -3.648e-02  1.362e-01  -0.268  0.78897    
## x42          2.787e-01  1.314e-01   2.120  0.03436 *  
## x43         -2.719e-01  1.329e-01  -2.045  0.04123 *  
## x44         -2.214e-01  1.321e-01  -1.677  0.09411 .  
## x45         -7.308e-02  1.309e-01  -0.558  0.57686    
## x46          8.252e-02  1.310e-01   0.630  0.52901    
## x47          1.309e-01  1.349e-01   0.970  0.33236    
## x48          1.691e-02  1.334e-01   0.127  0.89917    
## x49         -1.137e-01  1.390e-01  -0.818  0.41351    
## x50         -1.497e-01  1.295e-01  -1.156  0.24827    
## x51         -2.759e-01  1.305e-01  -2.114  0.03491 *  
## x52          8.536e-02  1.334e-01   0.640  0.52239    
## x53          1.160e-01  1.279e-01   0.907  0.36456    
## x54         -3.292e-02  1.315e-01  -0.250  0.80242    
## x55          1.115e-01  1.347e-01   0.827  0.40844    
## x56         -2.023e-01  1.309e-01  -1.546  0.12271    
## x57         -4.191e-02  1.302e-01  -0.322  0.74771    
## x58         -2.381e-01  1.321e-01  -1.803  0.07193 .  
## x59         -5.437e-01  1.320e-01  -4.118 4.31e-05 ***
## x60         -9.735e-02  1.411e-01  -0.690  0.49061    
## x61         -1.652e-01  1.333e-01  -1.239  0.21585    
## x62          1.380e-01  1.332e-01   1.037  0.30031    
## x63         -7.154e-02  1.327e-01  -0.539  0.59011    
## x64          4.150e-02  1.303e-01   0.319  0.75020    
## x65          4.623e-02  1.329e-01   0.348  0.72814    
## x66          2.264e-02  1.374e-01   0.165  0.86922    
## x67         -1.696e-02  1.295e-01  -0.131  0.89583    
## x68         -8.959e-02  1.284e-01  -0.698  0.48546    
## x69          2.565e-01  1.359e-01   1.887  0.05957 .  
## x70         -5.123e-02  1.358e-01  -0.377  0.70606    
## x71         -8.445e-02  1.397e-01  -0.605  0.54572    
## x72         -2.982e-02  1.364e-01  -0.219  0.82702    
## x73         -2.482e-01  1.324e-01  -1.874  0.06140 .  
## x74          1.848e-01  1.338e-01   1.381  0.16775    
## x75          2.625e-01  1.330e-01   1.974  0.04877 *  
## x76         -1.753e-01  1.341e-01  -1.308  0.19150    
## x77          1.845e-01  1.307e-01   1.411  0.15861    
## x78          1.212e-01  1.321e-01   0.917  0.35940    
## x79         -1.975e-01  1.320e-01  -1.496  0.13514    
## x80          1.575e-01  1.320e-01   1.194  0.23306    
## x81         -2.095e-01  1.298e-01  -1.614  0.10706    
## x82          1.895e-01  1.345e-01   1.409  0.15932    
## x83         -2.767e-02  1.328e-01  -0.208  0.83504    
## x84         -7.273e-02  1.292e-01  -0.563  0.57368    
## x85         -9.641e-02  1.319e-01  -0.731  0.46507    
## x86          2.781e-01  1.315e-01   2.114  0.03489 *  
## x87          1.705e-01  1.344e-01   1.268  0.20508    
## x88         -2.341e-01  1.282e-01  -1.827  0.06815 .  
## x89          5.146e-02  1.277e-01   0.403  0.68695    
## x90          5.663e-02  1.388e-01   0.408  0.68344    
## x91         -1.633e-01  1.349e-01  -1.210  0.22653    
## x92          2.494e-01  1.329e-01   1.877  0.06103 .  
## x93          1.449e-01  1.303e-01   1.112  0.26660    
## x94          2.023e-01  1.348e-01   1.501  0.13390    
## x95          5.046e-02  1.310e-01   0.385  0.70027    
## x96         -1.087e-02  1.351e-01  -0.080  0.93593    
## x97         -1.217e-01  1.321e-01  -0.921  0.35725    
## x98          4.116e-02  1.347e-01   0.306  0.76003    
## x99         -8.606e-02  1.340e-01  -0.642  0.52087    
## x100        -2.099e-01  1.307e-01  -1.605  0.10895    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9769 on 649 degrees of freedom
## Multiple R-squared:  0.4174, Adjusted R-squared:  0.3277 
## F-statistic: 4.651 on 100 and 649 DF,  p-value: < 2.2e-16

Il modello ottiene molti parametri non signnificativi; inoltre, come atteso per la collinearità, gli errori
standard dei parametri sono elevati. Notate inoltre che le stime dei parametri sono molto “distanti” dai valori veri.
Tuttavia, $\hat{\sigma}^2 =$ 0.977 indica che i residui dei dati di training sono abbastanza buoni.

In ogni modo, per verificare le performance predittive del modello, dobbiamo applicarlo sui dati di test indipendenti, ottenendo i seguenti risultati:

res <- dt_test$y - predict(ols_fit, newdata = dt_test)
mse <- setNames(c(summary(res), mean(res^2)),
                nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
print(mse)

##         Min.      1st Qu.       Median         Mean      3rd Qu.         Max. 
## -2.848756104 -0.734574284 -0.063600785 -0.008475534  0.777965582  3.123768708 
##    MeanSqErr 
##  1.222308290

ggp <- ggplot(data.frame(fit=predict(ols_fit, newdata = dt_test), obs=dt_test$y),
              mapping = aes(x = obs, y = fit)) +
  geom_point() +
  ggtitle("OLS: Osservati Vs. Previsti") +
  xlab("Y osservati") + ylab("Y previsti") + 
  geom_abline(slope = 1,intercept = 0, colour="red")
print(ggp)

I residui dei dati di test mostrano una variabilità più elevata rispetto ai residui dei dati di training.

Cercando un modello più parsimonioso magari potremo ottenere delle previsioni migliori.

19.3 Selezione Forward Stepwise

La selezione dei predittori tramite tecnoca forward stepwise comincia con un modello contenente pochi o nessun predittore, e quindi aggiunge al modello un predittore “significativo” alla volta fino a che avrà incluso nel modello tutti i predittori “significativi”. La procedura di selezione “forward stepwise” cerca di minimizzare una funzione-criterio di ottimalità (spesso AIC), e segue i seguenti passaggi:

Comincia con un “modello iniziale” (spesso il modello con “sola media, nessun predittore”) e calcola la funzione criterio
Aggiungi il predittore che magigormente riduce la funzione criterio
Aggiungi un altro predittore (se esiste) che maggiormente riduce la funzione criterio
Verifica che i predittori precedentemente inseriti nel modello possano essere rimossi (cioè, verifica se rimuovendo predittori inseriti precedentemente la funzione criterio si riduce); rimuovi questi predittori uno alla volta
Ci sono altri predittori che, una volta inseriti nel modello riducono la funzione criterio? Se sì, allora torna al passo 3.
Esci

Anche se molto vantaggioso in termini computazionali, per esempio rispetto alla selezione del miglior sottoinsieme (si veda dopo), il metodo Forward Stepwise non garantisce di trovare il miglior modello possibile tra tutti i modelli contenenti sottoinsiemi dei $p$ predittori. Per esempio, supponente che in un dato dataset con $p = 3$ predittori, il miglior modello possibile con una variabile contenga $X1$, e che il miglior modello possibile generale sia un modello con 2 variabili che contiene $X2$ e $X3$; in tal caso la selzione forward stepwise potrebbe fallire nella selezione del miglior modello possibile, perché nel secondo passaggio il metodo potrebbe non essere in grado di rimuovere $X1$.

library(MASS)

m_init <- lm(y ~ 1, data = dt_train)
upr <- paste("x",1:100, sep="", collapse=" + ")
upr <- as.formula(paste("~",upr))
forw_fit <- stepAIC(m_init, scope = list(upper = upr, lower = ~ 1) ,
                    direction = "both", trace = FALSE)
summary(forw_fit)

## 
## Call:
## lm(formula = y ~ x1 + x3 + x59 + x34 + x5 + x6 + x42 + x51 + 
##     x29 + x43 + x32 + x74 + x92 + x86 + x94 + x13 + x44 + x69 + 
##     x4 + x75 + x26 + x79 + x88 + x56 + x73 + x93 + x62 + x76 + 
##     x82 + x77 + x15 + x58, data = dt_train)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.69612 -0.64330 -0.00785  0.62150  2.64483 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   3.8289     0.3421  11.191  < 2e-16 ***
## x1            0.7044     0.1248   5.646 2.37e-08 ***
## x3           -1.9260     0.2798  -6.885 1.27e-11 ***
## x59          -0.5310     0.1224  -4.339 1.64e-05 ***
## x34           0.3865     0.1257   3.075  0.00219 ** 
## x5            1.2509     0.5197   2.407  0.01633 *  
## x6            0.2990     0.1246   2.400  0.01666 *  
## x42           0.3054     0.1205   2.534  0.01150 *  
## x51          -0.2725     0.1225  -2.224  0.02647 *  
## x29          -0.2672     0.1247  -2.143  0.03246 *  
## x43          -0.2341     0.1218  -1.923  0.05492 .  
## x32           0.3548     0.1240   2.862  0.00434 ** 
## x74           0.2268     0.1233   1.840  0.06620 .  
## x92           0.2464     0.1211   2.035  0.04221 *  
## x86           0.2344     0.1221   1.919  0.05536 .  
## x94           0.2432     0.1250   1.946  0.05206 .  
## x13           0.2491     0.1265   1.969  0.04929 *  
## x44          -0.2331     0.1226  -1.901  0.05770 .  
## x69           0.2310     0.1225   1.885  0.05985 .  
## x4           -0.7417     0.4011  -1.849  0.06486 .  
## x75           0.2296     0.1230   1.866  0.06250 .  
## x26          -0.1889     0.1236  -1.528  0.12687    
## x79          -0.1934     0.1222  -1.583  0.11393    
## x88          -0.2171     0.1203  -1.804  0.07168 .  
## x56          -0.2205     0.1210  -1.823  0.06879 .  
## x73          -0.2171     0.1230  -1.766  0.07790 .  
## x93           0.1694     0.1217   1.392  0.16437    
## x62           0.2072     0.1222   1.696  0.09026 .  
## x76          -0.2203     0.1232  -1.788  0.07417 .  
## x82           0.2091     0.1244   1.681  0.09320 .  
## x77           0.1745     0.1219   1.431  0.15280    
## x15           0.1934     0.1262   1.533  0.12581    
## x58          -0.1706     0.1228  -1.389  0.16522    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9531 on 717 degrees of freedom
## Multiple R-squared:  0.3875, Adjusted R-squared:  0.3601 
## F-statistic: 14.17 on 32 and 717 DF,  p-value: < 2.2e-16

Nel nostro caso di esempio, le stime dei parametri sono abbastanza prossime ai veri valori dei parametri.
Ci sono però un po’ troppe variabili selezionate dalla procedura (rispetto al modello vero). Questo potrebbe forse dipendere dalla multicollinearità.

Le performance predittive sono:

# Grafico valori Osservati Vs. Previsti
ggp <- ggplot(data.frame(fit=predict(forw_fit, newdata = dt_test), obs=dt_test$y),
              mapping = aes(x = obs, y = fit)) +
  geom_point() +
  ggtitle("Forward Stepwise: Osservati Vs. Previsti") +
  xlab("Y osservati") + ylab("Y previsti") + 
  geom_abline(slope = 1,intercept = 0, colour="red")
print(ggp)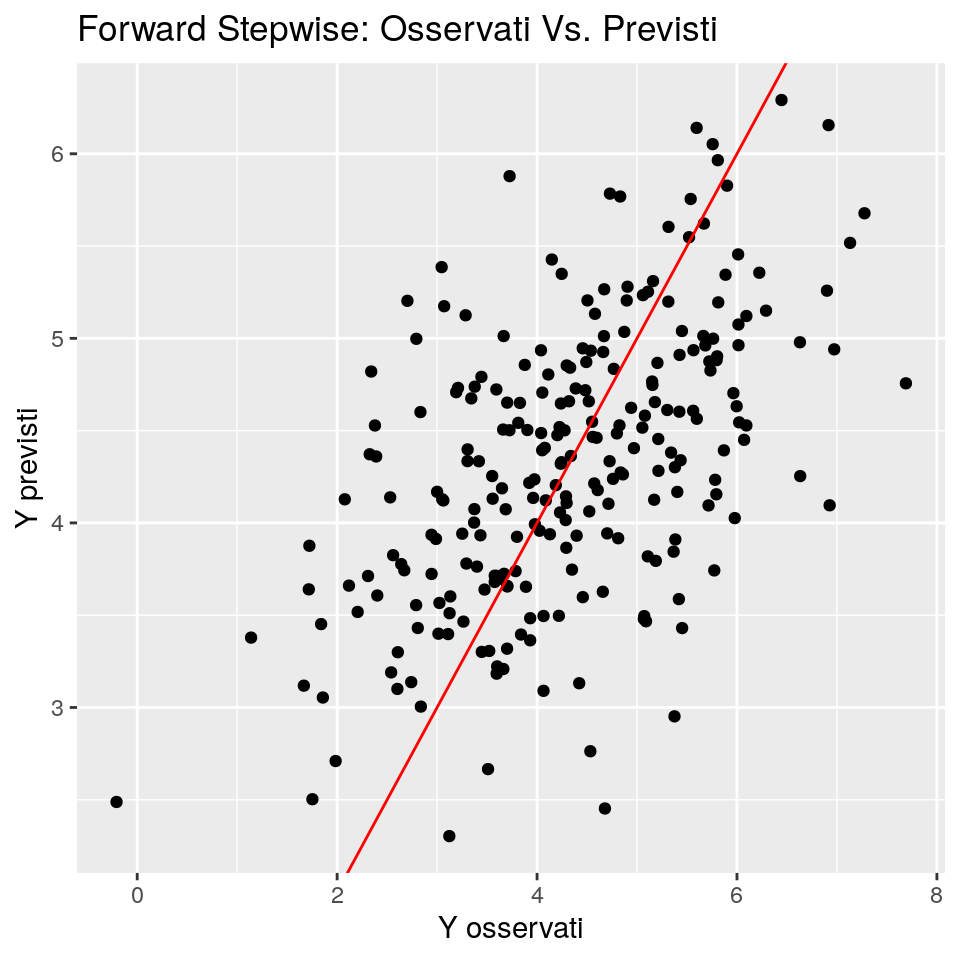

y_pred_forw <- predict(forw_fit, newdata = dt_test)
res <- dt_test$y - y_pred_forw
mse1 <- setNames(c(summary(res), mean(res^2)),
                 nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
mse <- rbind(mse, mse1)
rownames(mse)[1] <- "OLS"
rownames(mse)[nrow(mse)] <- "Forward"
mse

##              Min.    1st Qu.      Median         Mean   3rd Qu.     Max.
## OLS     -2.848756 -0.7345743 -0.06360079 -0.008475534 0.7779656 3.123769
## Forward -2.694752 -0.6807069 -0.06648533 -0.008589938 0.6807813 2.933698
##         MeanSqErr
## OLS      1.222308
## Forward  1.126742

In questo caso la selezione forward stepwise ritorna risultati abbastanza buoni. Il miglior modello selezionato è un poco “ridondante” (almeno rispetto al modello ideale), ma mostra buone performance predittive.

19.4 Selezione Backward Stepwise

Diveramente dalla selezione forward stepwise, la selezione backward stepwise inizia con il modello ai minimi quadrati contenente tutti i predittori, e quindi rimuove iterativamente i preittori meno “utili”, uno alla volta. Anche la procedura di selezione Backward stepwise cerca di minimizzare una funzione-criterio di ottimalità (spesso AIC), e prosegue in questo modo:

Inizia con un “modello iniziale” (spesso il modello con “tutti i predittori”) e calcola la funzione criterio
Rimuovi il predittore che riduce maggiormente a funzione criterio
Rimuovi un altro predittore (se esiste) che riduce maggiormente la funzione criterio
Verifica se i predittori precedentemente rumossi possono essere reintrodotti nel modello (cioè, verifica se aggiungendo una variabile alla volta di quelle precedenemente rimosse la funzione criterio si riduce); aggiungi queste variabili una alla volta
Ci sono alti predittori che quando rimossi dal modello riducono la funzione criterio? Se sì, torna al passo 3.
Esci

Come per la selezione forward stepwise, la selezione backward stepwise non garantisce di ottenere il miglior modello contenente un sottoinsieme dei $p$ predittori. A differenza della forward stepwise, la selezione backward richiede che la dimensione del campione $n$ sia maggiore del numero di variabili $p$ (per poter adattare il modello iniziale). In ogni modo, la procedura backward stepwise usualmente ottiene risultati migliori rispetto alla borward.

m_init <- lm(y ~ ., data = dt_train)
back_fit <- stepAIC(m_init, scope = list(upper = ~ ., lower = ~ 1) ,
                    direction = "both", trace = FALSE)
summary(back_fit)

## 
## Call:
## lm(formula = y ~ x1 + x2 + x4 + x5 + x6 + x8 + x13 + x15 + x16 + 
##     x22 + x26 + x29 + x30 + x32 + x40 + x45 + x51 + x59 + x68 + 
##     x69 + x75 + x81 + x82 + x83 + x86 + x87 + x94, data = dt_train)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.95193 -0.67439 -0.03723  0.63497  2.78239 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.72416    0.34234  10.878  < 2e-16 ***
## x1          -0.28925    0.06055  -4.777 2.16e-06 ***
## x2           1.15323    0.14540   7.931 8.26e-15 ***
## x4           2.29936    0.21682  10.605  < 2e-16 ***
## x5          -2.69594    0.27440  -9.825  < 2e-16 ***
## x6           0.39359    0.12794   3.076 0.002175 ** 
## x8          -0.26176    0.12741  -2.054 0.040289 *  
## x13          0.22864    0.12721   1.797 0.072704 .  
## x15          0.18794    0.12723   1.477 0.140071    
## x16          0.20962    0.12403   1.690 0.091439 .  
## x22          0.19068    0.12422   1.535 0.125212    
## x26         -0.17761    0.12301  -1.444 0.149219    
## x29         -0.28446    0.12550  -2.267 0.023707 *  
## x30         -0.27787    0.12661  -2.195 0.028511 *  
## x32          0.38858    0.12768   3.043 0.002425 ** 
## x40          0.19775    0.12652   1.563 0.118505    
## x45         -0.20860    0.12499  -1.669 0.095572 .  
## x51         -0.20463    0.12404  -1.650 0.099444 .  
## x59         -0.43285    0.12513  -3.459 0.000573 ***
## x68         -0.26278    0.12345  -2.129 0.033630 *  
## x69          0.19663    0.12657   1.554 0.120740    
## x75          0.19255    0.12738   1.512 0.131083    
## x81         -0.17202    0.12239  -1.406 0.160287    
## x82          0.27709    0.12636   2.193 0.028643 *  
## x83          0.21754    0.12327   1.765 0.078032 .  
## x86          0.19022    0.12308   1.546 0.122660    
## x87          0.18358    0.12540   1.464 0.143618    
## x94          0.23738    0.12970   1.830 0.067615 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.978 on 722 degrees of freedom
## Multiple R-squared:  0.3892, Adjusted R-squared:  0.3664 
## F-statistic: 17.04 on 27 and 722 DF,  p-value: < 2.2e-16

Also in this case, the parameter estimates are almost close to the true parameter values.
Perhaps too many variables were selected by the procedure. Maybe, it could depend from the multicollinearity too.

The predictive performaces:

# Grafico valori Osservati Vs. Previsti
ggp <- ggplot(data.frame(fit=predict(back_fit, newdata = dt_test), obs=dt_test$y),
              mapping = aes(x = obs, y = fit)) +
  geom_point() +
  ggtitle("Backward Stepwise: Osservati Vs. Previsti") +
  xlab("Y osservati") + ylab("Y previsti") + 
  geom_abline(slope = 1,intercept = 0, colour="red")
print(ggp)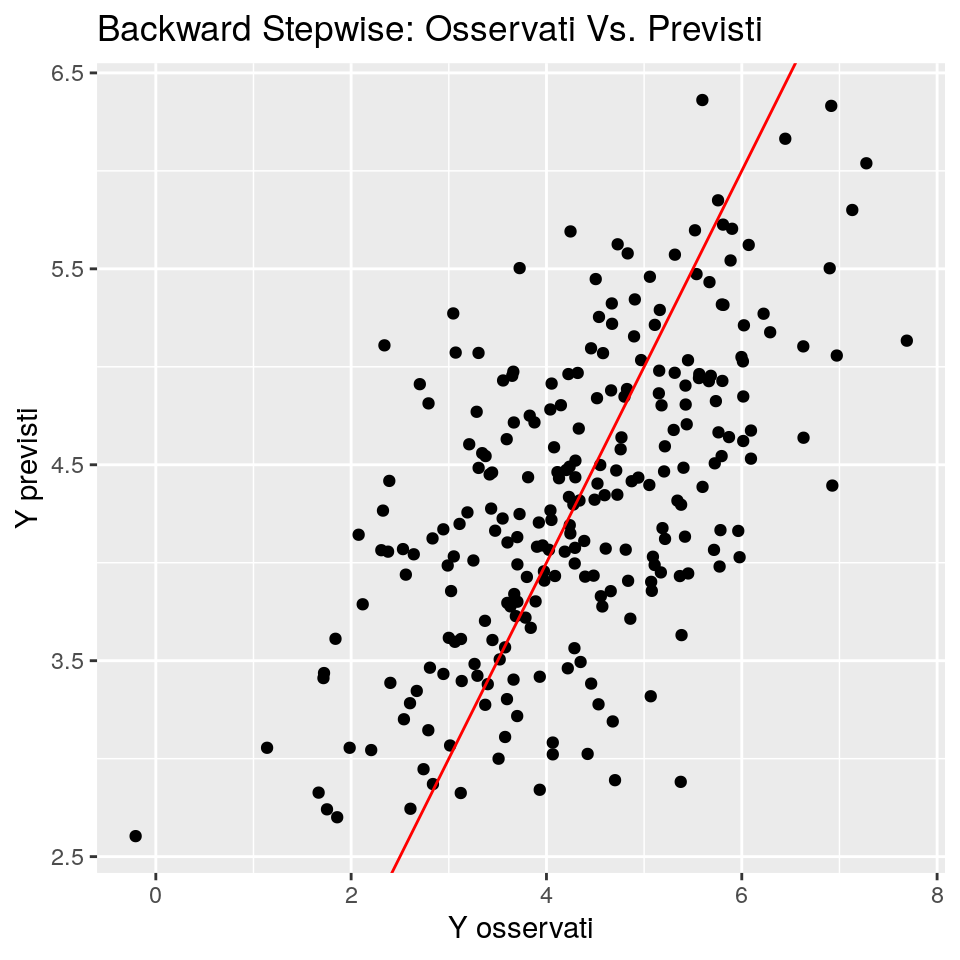

y_pred_back <- predict(back_fit, newdata = dt_test)
res <- dt_test$y - y_pred_back
mse1 <- setNames(c(summary(res), mean(res^2)), nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
mse <- rbind(mse, mse1)
rownames(mse)[nrow(mse)] <- "Backward"
mse

##               Min.    1st Qu.       Median         Mean   3rd Qu.     Max.
## OLS      -2.848756 -0.7345743 -0.063600785 -0.008475534 0.7779656 3.123769
## Forward  -2.694752 -0.6807069 -0.066485330 -0.008589938 0.6807813 2.933698
## Backward -2.811408 -0.6704336 -0.006818937  0.002312087 0.7294619 2.556570
##          MeanSqErr
## OLS       1.222308
## Forward   1.126742
## Backward  1.024182

In questo caso, il Backward Stepwise porta a risultati leggermente peggiori del Forward.

19.5 Selezione del Miglior Sottoinsieme (Best Subset)

Nella selezione del miglior sottoinsieme si adatta una regressione ai minimi quadrati separata per ogni possibile combinazione dei $p$ predittori. Si adattano cioè tutti i modelli che contengono esattamente un predittore, tutti i modelli che contengono esattamente due predittori, e via di seguito. Si identifica quindi il modello “migliore” rispetto ad un criterio di ottimalità dato (typicamente, l’R-quadro aggiustato, BIC, AIC, o Cp di Mallows).

Se la selezione del miglior sottoinsieme è un approccio semplice e concettualmente attraente, esso soffre tuttavia di limitazioni a livello computazionale. Il numero di modelli possibili che devono essere elaborati cresce rapidamente mano a mano che il numero di predittori potenziali cresce. Con $p$ = 10, ci sono approssimativamente 1,000 modelli possibili da considerare; di conseguenza l’approccio diventa computazionalmente intrattabile per un numero di variabili non molto grande (attorno alle 40). Perdipiù, la selezione del miglior sottoinsieme non ottiene buoni risultati in in situazioni in cui $p > n$, cioè quando il numero di predittori è maggiore del numero di casi, nonché quando alcuni dei predittori sono foretemente correlati tra loro.

In ogni mdo, il package leaps contiene la funzione regsubsets() che implementa l’approccio del miglior sottoinsieme:

library(leaps)

# Esegue una ricerca esaustiva del miglior sottoinsieme di predittori per il modello (vedere il parametro 'method')
nvmax <- 20
dt_t <- dt_train
dt_train <- dt_train[, c(1:35,101)]
bs_fit <- regsubsets(x = dt_train[, 1:(ncol(dt_train)-1)], y = dt_train[, ncol(dt_train)], method = "exhaustive", nvmax = nvmax, really.big = TRUE) 
l <- summary(bs_fit)

# Grafico dei valori dell'indice CP
ggp <- ggplot(data = data.frame(size=1:nvmax, cp=l$cp), mapping = aes(x = size, y = cp)) +
  geom_point() +
  xlab("Dimensione modello") + ylab("Cp di Mallows")
print(ggp)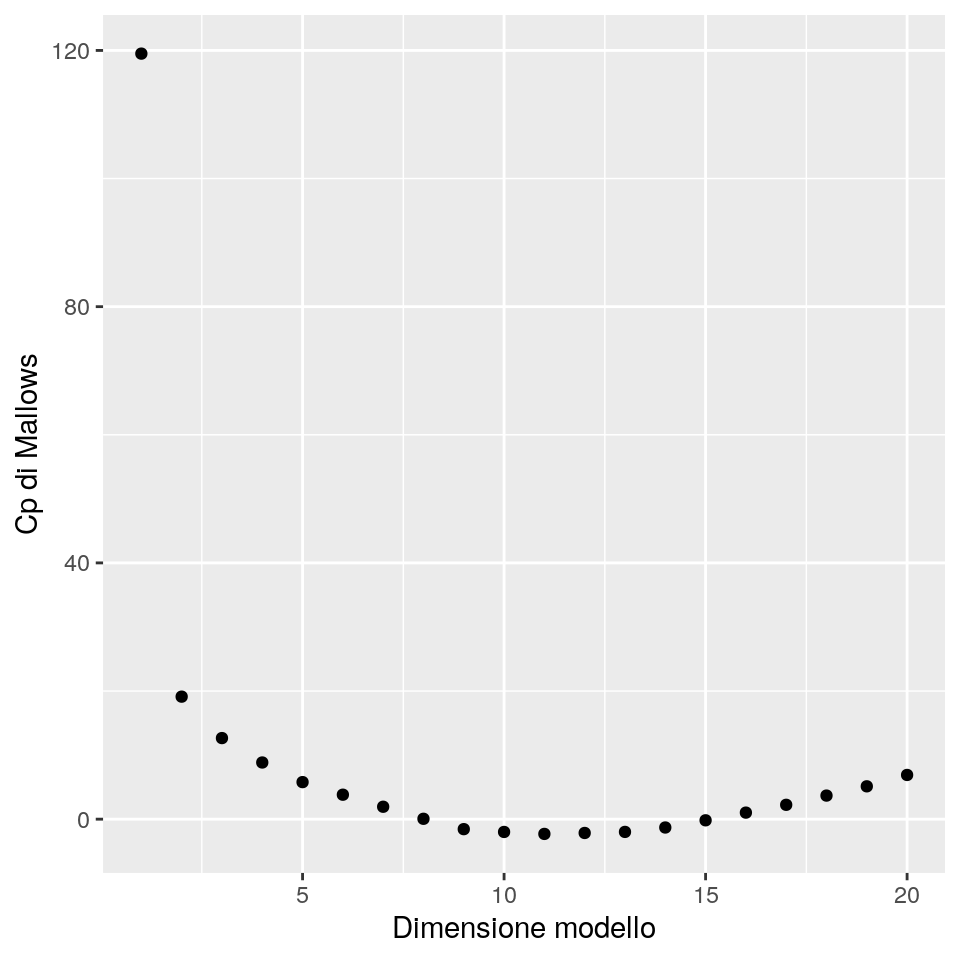

Nota: Il valore del Cp di Mallows è $Cp = \frac{RSS_p}{s^2}-(n - 2p)$, dove $s^2$ è la deviazione standard dei residui calcolata sul modello più completo, $p$ è il numero di parametri stimati nel modello, e $n$ è la dimensione campionaria (numero di righe dei dati di training).
Selezioneremo il miglior modello secondo $Cp$:

# Seleziona i predittori del miglior modello
bestfeat <- l$which[which.min(l$cp), ]
# Aggiungi la variabile dipendente
bestfeat <- c(bestfeat[-1], TRUE)

Infine, stimiamo e testiamo il miglior modello selezionato

m_bestsubset <- lm(y ~ ., data = dt_train[, bestfeat])
summary(m_bestsubset)

## 
## Call:
## lm(formula = y ~ ., data = dt_train[, bestfeat])
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.98326 -0.62538 -0.01706  0.70044  2.88287 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     3.9487     0.1961  20.136   <2e-16 ***
## x1            563.3218   366.8198   1.536   0.1250    
## x2           -562.6166   366.8241  -1.534   0.1255    
## x3          -1127.1746   733.6438  -1.536   0.1249    
## x4          -1688.5911  1100.4569  -1.534   0.1253    
## x5           2251.7889  1467.2801   1.535   0.1253    
## x6              0.3021     0.1278   2.364   0.0183 *  
## x13             0.2642     0.1297   2.036   0.0421 *  
## x26            -0.2473     0.1257  -1.968   0.0495 *  
## x29            -0.2581     0.1284  -2.011   0.0447 *  
## x32             0.2508     0.1254   1.999   0.0460 *  
## x34             0.3646     0.1282   2.843   0.0046 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9912 on 738 degrees of freedom
## Multiple R-squared:  0.3181, Adjusted R-squared:  0.3079 
## F-statistic: 31.29 on 11 and 738 DF,  p-value: < 2.2e-16

Il modello sui dati di training sembra selezionare troppe variabili, quasi tutti i parametri stimati sono molto distanti dai veri valori dei parametri e mostrano un valore di p-value molto alto. Questo risultato può dipendenre dall’elevata multicollinearità.

Vediamo ora le performance predittive:

# Plots Observed Vs. Predicted values
ggp <- ggplot(data = data.frame(fit=predict(m_bestsubset, newdata = dt_test), obs=dt_test$y), mapping = aes(x = obs, y = fit)) +
  geom_point() +
  ggtitle("Best Subset: Osservati Vs. Previsti") +
  xlab("Y osservati") + ylab("Y previsti") + 
  geom_abline(slope = 1,intercept = 0, colour="red")
print(ggp)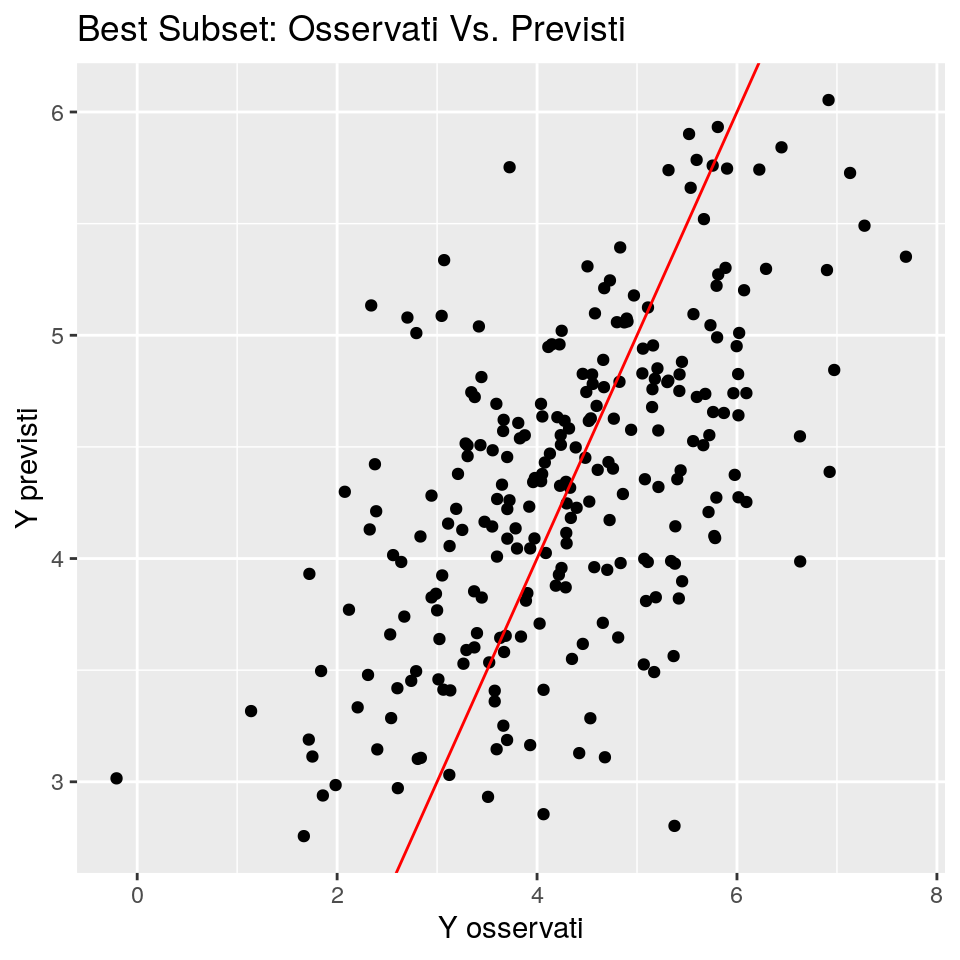

y_pred_bestsubset <- predict(m_bestsubset, dt_test[, bestfeat])
res <- dt_test$y - y_pred_bestsubset
mse1 <- setNames(c(summary(res), mean(res^2)), nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
mse <- rbind(mse, mse1)
rownames(mse)[nrow(mse)] <- "Best subset"
mse

##                  Min.    1st Qu.       Median         Mean   3rd Qu.     Max.
## OLS         -2.848756 -0.7345743 -0.063600785 -0.008475534 0.7779656 3.123769
## Forward     -2.694752 -0.6807069 -0.066485330 -0.008589938 0.6807813 2.933698
## Backward    -2.811408 -0.6704336 -0.006818937  0.002312087 0.7294619 2.556570
## Best subset -3.222127 -0.6878269 -0.092767711 -0.011493783 0.6494942 2.645342
##             MeanSqErr
## OLS          1.222308
## Forward      1.126742
## Backward     1.024182
## Best subset  1.064705

dt_train <- dt_t
rm(dt_t)

Best subset sembra prevedere bene o non peggio degli altri metodi. Questo può dipendere dal gran numero di predittori selezionati dai metodi, che produce un overfitting sui dati: i metodi qui sopra prevedono bene i dati di training, ma non i dati di test, anche se questi provengono dallo stesso processo (per costruzione).
Si noti che questo risultato può cambiare cambiando il criterio per selezionare il miglior modello (per esempio, AIC o BIC invece del Cp di Mallows).

19.6 Regressione Ridge

Quando si hanno molti predittori disponibili, e quando esiste una elevata collinearità tra i predittori, allora le stime possono diventare instabili e meno attendibili.

Un metodo per risolvere questo problema è quello di adattare un modello contenente tutti i $p$ predittori usando una tecnica che “vincola” o “regolarizza” le stime dei coefficienti, o equivalentemente, che “cotringe” (“shrink”) le stime dei coefficienti verso zero. Spingere le stime dei coefficienti ha l’effetto di ridurre significativamente la varianza dei coefficienti. La tecnica più nota per spingere i coefficienti della regressione verso zero è la regressione “ridge”.

Nella regressione ridge i coefficienti sono stimati minimizzando una quantità leggermente differente, rispetto ai minimi quadrati. In particolare, la funzione obiettivo nella regressione ridge è una versione “penalizzata” della somma dei quadrati delle deviazioni usata nei minimi quadrati. La penalizzazione (chiamata “shrinkage penalty”), è piccola quando i coefficienti sono prossimi a zero, e quindi ha l’effetto di costringere le stime verso lo zero. Nella funzione obiettivo trviamo anche un parametro di tuning che regola l’ammontare dello “shrinkage”.
In forma matematica, la regressione ridge cerca i valori $\hat{\underline{\beta}}=(\beta_0, \beta_1, \dots, \beta_p)^T$ che minimizzano il seguente criterio di minimi quadrati modificato:

\[\sum_{i=1}^n \left(y_i - \underline{x}_i^T\underline{\beta} \right)^2 + \lambda \sum_{j=1}^p \beta_j^2\]

Dove $\lambda$ è il parametro di penalizzazione e i predittori sono usualmente standardizzati.
La selezione di un buon valore di $\lambda$ è critica, ed è fatta tipicamente tramite cross-validation.

La regressione ridge produce stime dei coefficienti meno variabili e meno correlate al costo di un leggero aumento nella distorsione della stima.
Come già detto la regressione ridge tende a “spingere verso lo zero” coefficienti stimati.
Si noti che la regressione ridge non penalizza il termine di intercetta.

La regressione ridge è stata originariamente sviluppata per risolvere il problema indotto da predittori fortemente correlati (la cosiddetta multicollinearità). Infatti, le stime ai minimi quadrati dell’errore standard error dei coefficienti può essere espressa come $s^2/((n - 1) \cdot Var(x_j) \cdot 1/(1 - R_j)$, dove $s^2$ è la varianza residua, $Var(x_j)$ è la varianza del $j$-mo predittore, e $R_j$ è il coefficiente di denominazione della regressione del $j$-mo predittore con i rimanenti predittori. Il vattore $1/(1 - R_j)$ è chiamato variance inflation factor (VIF: fattore di inflazionamento della varianza).

Nel nostro esempio, il VIF per il primo predittore è dato da:

1/(1 - summary(lm(x1 ~ ., data = dt_train[,1:100]))$r.squared)

## [1] 274114480

che è molto elevato! La soglia usata più comunemente per il VIF è 10.

In R, è disponibile la funzione lm.ridge() dal package MASS. Questa funzione esegue la regressione ridge e fornisce strumenti per selezionare il miglior valore di $\lambda$:

ridge_fit <- lm.ridge(y ~ ., data = dt_train, lambda = seq(0, 400, by = 0.01))
select(ridge_fit) ## Nota: HKB e L-W sono stimatori alternativi del parametro ridge

## modified HKB estimator is 0.000228431 
## modified L-W estimator is 158.045 
## smallest value of GCV  at 268.57

# Grafico dei valori di Lambda GCV (generalized cross-validation) con RSS (residual sum of squares:
ggp <- ggplot(data = as.data.frame(ridge_fit[c("lambda", "GCV")]),
              mapping = aes(x=lambda, y=GCV)) +
  geom_line() +
  xlab("Lambda (parametro penalizzazione)") + ylab("Valori di generalized Cross-Validation (GCV)")
print(ggp)

ridge_fit <- lm.ridge(y ~ ., data = dt_train,
                      lambda = ridge_fit$GCV[which(ridge_fit$GCV == min(ridge_fit$GCV))])

Poiché non c’è un metodo predict implementato, dobbiamo calcolarci le previsioni:

y_pred_ridge <- as.numeric(cbind(1, as.matrix(dt_test[, 1:(ncol(dt) - 1)])) %*% coef(ridge_fit))

Ed ora le performance predittive:

# Plots Observed Vs. Predicted values
ggp <- ggplot(data = data.frame(fit=y_pred_ridge, obs=dt_test$y),
              mapping = aes(x = obs, y = fit)) +
  geom_point() +
  ggtitle("Regressione ridge: Osservati Vs. Previsti") +
  xlab("Y osservati") + ylab("Y previsti") + 
  geom_abline(slope = 1,intercept = 0, colour="red")
print(ggp)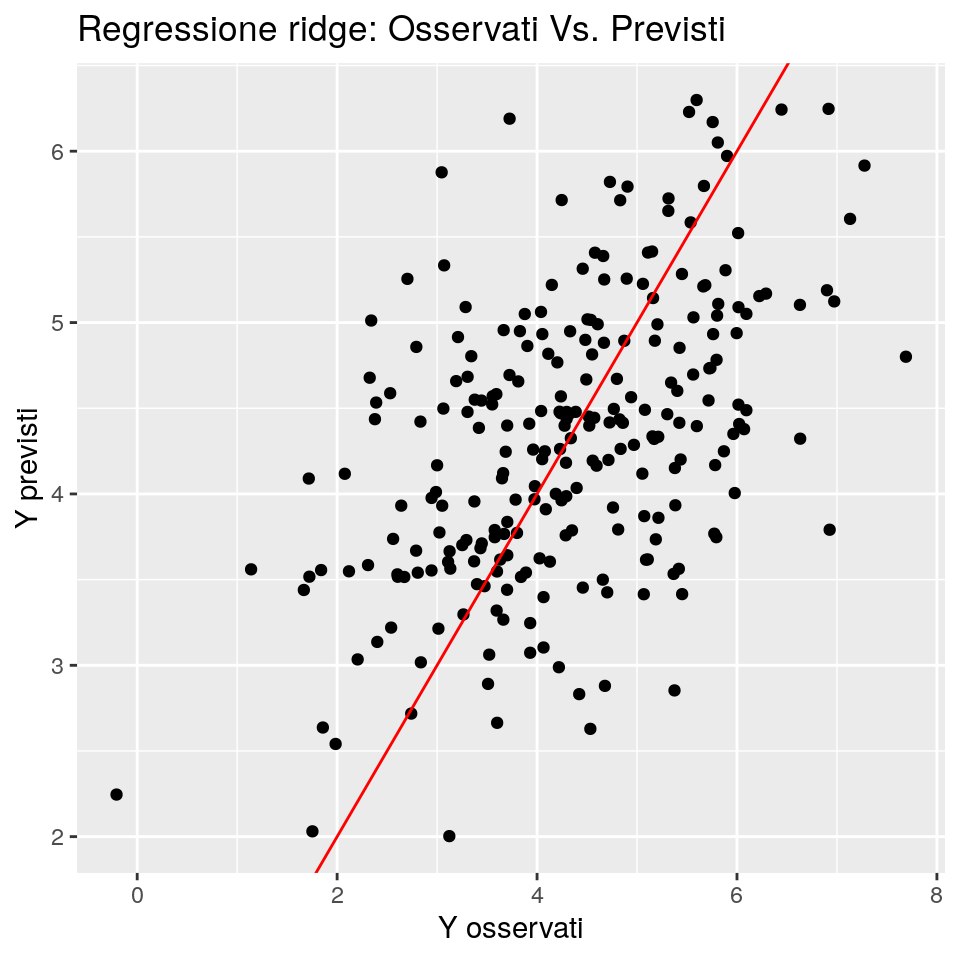

Il corrispondente mse è dato da

res <- dt_test$y - y_pred_ridge
mse1 <- setNames(c(summary(res), mean(res^2)),
                 nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
mse <- rbind(mse, mse1)
rownames(mse)[nrow(mse)] <- "Ridge"
mse

##                  Min.    1st Qu.       Median         Mean   3rd Qu.     Max.
## OLS         -2.848756 -0.7345743 -0.063600785 -0.008475534 0.7779656 3.123769
## Forward     -2.694752 -0.6807069 -0.066485330 -0.008589938 0.6807813 2.933698
## Backward    -2.811408 -0.6704336 -0.006818937  0.002312087 0.7294619 2.556570
## Best subset -3.222127 -0.6878269 -0.092767711 -0.011493783 0.6494942 2.645342
## Ridge       -2.831095 -0.7317479 -0.069166253 -0.008504460 0.7913391 3.136069
##             MeanSqErr
## OLS          1.222308
## Forward      1.126742
## Backward     1.024182
## Best subset  1.064705
## Ridge        1.218283

Possiamo vedere che, almeno per questo caso, la regressione ridge non è in grado di produrre previsioni molto accurate. Ciò è probabilmente dovuto ad un effetto di overfitting, poiché non è stato applicata alcuna selezione delle variabili. Potremmo provare prima a selezionare le variabili usandouno dei metodi visti in precedenza, e quindi, se compare una collinearità tra i predittori, applicare la regressione ridge.

Infine, mostriamo le stime dei coefficienti, confrontate con le stime OLS:

cbind(coef(ridge_fit),coef(ols_fit))

##              [,1]          [,2]
##       4.393367344  4.404065e+00
## x1    0.445721313  2.880663e+02
## x2    0.307368598 -2.873190e+02
## x3   -1.426739483 -5.766728e+02
## x4    0.038520959 -8.628190e+02
## x5    0.199891366  1.150682e+03
## x6    0.319586961  3.246824e-01
## x7    0.065271957  6.211367e-02
## x8   -0.195457982 -1.944821e-01
## x9   -0.049996703 -5.208436e-02
## x10  -0.039364373 -3.370574e-02
## x11  -0.042975229 -4.370113e-02
## x12  -0.174834678 -1.770139e-01
## x13   0.262260600  2.674207e-01
## x14   0.062744022  6.129948e-02
## x15   0.198770432  1.960977e-01
## x16   0.172812245  1.658083e-01
## x17   0.132559357  1.293402e-01
## x18   0.004120894  3.966045e-03
## x19  -0.005214984 -1.948873e-03
## x20  -0.048355501 -4.912650e-02
## x21   0.022740918  2.218679e-02
## x22   0.020275703  1.878258e-02
## x23   0.084881953  8.421086e-02
## x24  -0.002852419 -2.245098e-03
## x25   0.060087142  5.546734e-02
## x26  -0.209616064 -2.142061e-01
## x27   0.091135885  8.894021e-02
## x28  -0.123969632 -1.250152e-01
## x29  -0.301634814 -3.115027e-01
## x30  -0.065656878 -5.999697e-02
## x31   0.004064208 -2.528932e-03
## x32   0.363921891  3.636581e-01
## x33  -0.102846811 -1.028048e-01
## x34   0.437407296  4.451084e-01
## x35   0.020718651  1.965767e-02
## x36  -0.020250957 -2.161993e-02
## x37  -0.112271321 -1.129653e-01
## x38  -0.150984939 -1.509616e-01
## x39   0.006013488  3.628922e-03
## x40   0.142283257  1.417113e-01
## x41  -0.031486140 -3.647643e-02
## x42   0.279483266  2.787121e-01
## x43  -0.272730156 -2.718957e-01
## x44  -0.226047760 -2.214330e-01
## x45  -0.071330748 -7.308547e-02
## x46   0.084571817  8.251879e-02
## x47   0.130910985  1.308526e-01
## x48   0.020796240  1.690671e-02
## x49  -0.117682841 -1.137166e-01
## x50  -0.152018858 -1.496932e-01
## x51  -0.276198807 -2.758667e-01
## x52   0.082235683  8.536429e-02
## x53   0.114306132  1.160372e-01
## x54  -0.031259602 -3.291583e-02
## x55   0.109390839  1.114602e-01
## x56  -0.206114327 -2.023416e-01
## x57  -0.039147350 -4.190874e-02
## x58  -0.236089434 -2.381457e-01
## x59  -0.550219225 -5.437261e-01
## x60  -0.095610399 -9.735339e-02
## x61  -0.167515722 -1.651817e-01
## x62   0.139809064  1.380255e-01
## x63  -0.069701224 -7.154300e-02
## x64   0.040222373  4.150244e-02
## x65   0.039831041  4.623047e-02
## x66   0.019993369  2.263828e-02
## x67  -0.019924696 -1.695538e-02
## x68  -0.092976337 -8.959357e-02
## x69   0.265729441  2.565096e-01
## x70  -0.054068671 -5.123270e-02
## x71  -0.089019399 -8.445003e-02
## x72  -0.028118548 -2.981941e-02
## x73  -0.247985358 -2.481738e-01
## x74   0.184070506  1.848306e-01
## x75   0.265030987  2.625425e-01
## x76  -0.177596750 -1.753274e-01
## x77   0.186433594  1.845091e-01
## x78   0.128454580  1.211823e-01
## x79  -0.195487029 -1.975019e-01
## x80   0.154643005  1.575192e-01
## x81  -0.212866891 -2.094859e-01
## x82   0.193430100  1.895278e-01
## x83  -0.024180793 -2.766562e-02
## x84  -0.077245426 -7.272684e-02
## x85  -0.092440636 -9.640484e-02
## x86   0.278349789  2.780803e-01
## x87   0.168327677  1.705130e-01
## x88  -0.231158672 -2.341440e-01
## x89   0.047953452  5.146481e-02
## x90   0.063632789  5.662787e-02
## x91  -0.167611728 -1.633315e-01
## x92   0.247374296  2.493911e-01
## x93   0.139428596  1.448978e-01
## x94   0.203483381  2.023258e-01
## x95   0.047318476  5.045634e-02
## x96  -0.012011641 -1.086802e-02
## x97  -0.118818274 -1.216565e-01
## x98   0.046745815  4.116098e-02
## x99  -0.087270656 -8.605787e-02
## x100 -0.212504669 -2.098590e-01

Come possiamo vedere, i coefficienti stimati sono spesso più simili ai coefficienti veri di molte delle altre tecniche usate in precedenza.

19.7 Regressione delle Componenti Principali (Principal Components Regression)

Esploreremo ora due metodi che trasformano i predittori e quindi adattano un modello ai minimi quadrati usando le variabili trasformate. Il primo approccio è chiamato regressione delle componenti principali (principal component regression, PCR), che dapprima costruisce le componenti principali della matrice delle variabili $X$, e quindi usa queste ultime come predittori in un modello ai minimi quadrati lineare. In PCR si assume quindi che le direzioni in cui $X1$,…,$Xp$ mostrano “il grosso” della variabilità siano le direzioni più associate con $Y$. Mentre questo assunto non è garantito sia vero, si dimostra spesso essere una approssimazione ragionevole.

In PCR, il numero di componenti principali è tipicamente scelto tramite cross- validation. Il package pls contiene una funzione, pcr(), che implementa l’approccio appena descritto:

library(pls)

pcr_fit <- pcr(y ~ ., data = dt_train, validation = "CV")

Selezioniamo ora il numero di componenti (tramite CV)

# Grafico i valori delle componenti CV coi corrispondenti RSS:
ggp <- ggplot(data = data.frame(comps=1:100, t(pcr_fit$validation$PRESS)),
              mapping = aes(x=comps, y=y)) +
  geom_line() +
  xlab("Numero di componenti") + ylab("Valori di Cross-Validation (CV)")
print(ggp)

(ncomp <- which.min(pcr_fit$validation$PRESS))

## [1] 68

Sorprendentemente, il numero di componenti selezionati da PCR è uguale a 68 (per la definizione della matrice dei predittori, c’è una sola variabile indipendente correlata con le altre, e circa 94 predittori inutili). Possiamo qindi calcolare i valori previsti

y_pred_pcr <- as.vector(predict(pcr_fit, dt_test, ncomp = ncomp))
res <- dt_test$y - y_pred_pcr
mse1 <- setNames(c(summary(res), mean(res^2)),
                 nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
mse <- rbind(mse, mse1)
rownames(mse)[nrow(mse)] <- "PCR"
mse

##                  Min.    1st Qu.       Median         Mean   3rd Qu.     Max.
## OLS         -2.848756 -0.7345743 -0.063600785 -0.008475534 0.7779656 3.123769
## Forward     -2.694752 -0.6807069 -0.066485330 -0.008589938 0.6807813 2.933698
## Backward    -2.811408 -0.6704336 -0.006818937  0.002312087 0.7294619 2.556570
## Best subset -3.222127 -0.6878269 -0.092767711 -0.011493783 0.6494942 2.645342
## Ridge       -2.831095 -0.7317479 -0.069166253 -0.008504460 0.7913391 3.136069
## PCR         -3.001682 -0.7495731 -0.003277450 -0.029553171 0.6997885 2.625501
##             MeanSqErr
## OLS          1.222308
## Forward      1.126742
## Backward     1.024182
## Best subset  1.064705
## Ridge        1.218283
## PCR          1.121846

# Grafico dei dati Osservati Vs. Previsti
ggp <- ggplot(data = data.frame(fit=y_pred_pcr, obs=dt_test$y),
              mapping = aes(x = obs, y = fit)) +
  geom_point() +
  ggtitle("PCR: Osservati Vs. Previsti") +
  xlab("Y osservati") + ylab("Y previsti") + 
  geom_abline(slope = 1,intercept = 0, colour="red")
print(ggp)

In questo caso, i risultati sono migliori di quelli dell’OLS e del backward e forward stepwise.
Un possibile passo avanti potrebbe essere quello di provare a ridurre il modello partendo dalla matrice delle 68 componenti principali.

19.8 Minimi Quadrati Parziali (Partial Least Squares: PLS)

Come abbiamo già puntualizzato, in PCR non si ha garanzia che le direzioni che meglio “spiegano” i predittori siano anche le migliori direzioni da usare per per prevedere la riposta. In altre parole, non è usata la rispsta $Y$ quando si cercano le componenti.

I minimi quadrati parziali (Partial least squares; PLS), invece, identificano le componenti con un approccio “supervisionato”, cioè, usano la risposta $Y$ per identificare nuove feature che, non solo approssimino bene le “vecchie” feature, ma che anche siano relazionate con la risposta. Detto in parole povere, l’approccio PLS cerca le direzioni che aiutino a “spiegare” sia la risposta, sia i predittori. Come per il PCR, il numero direzioni ai minimi quadrati parziali usate in PLS è un parametro di tuning usualmente scelto tramite cross-validation. Concretamente, PLS “spezza” il modello in due “blocchi”:
$X=TP^T + E$
$Y=UQ^T + F$
Dove $E$ e $F$ sono matrici di errori, $P$ e $Q$ sono pesi fattoriali, e $T$ e $U$ sono punteggi fattoriali (factor scores).
PLS cerca di massimizzare la correlazione tra $T$ e $U$.
$Y$ può essere multivariata.
PLS può anche operare senza problemi con dati in cui il numero di casi $n$ è molto inferiore al numero $p$ di variabili indipendenti (per es., analisi dello spettro NIR)

pls_fit <- as.vector(plsr(y ~ ., data = dt_train, validation = "CV"))
# Grafico del valore del numero di componenti CV con RSS:
ggp <- ggplot(data = data.frame(comps=1:100, t(pls_fit$validation$PRESS)),
              mapping = aes(x=comps, y=y)) +
  geom_line() +
  xlab("Numero di componenti") + ylab("Valori di Cross-Validation (CV)")
print(ggp)

(ncomp <- which.min(pls_fit$validation$PRESS))

## [1] 2

y_pred_pls <- predict(pls_fit, dt_test, ncomp = ncomp)
res <- dt_test$y - y_pred_pls
mse1 <- setNames(c(summary(res), mean(res^2)),
                 nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
mse <- rbind(mse, mse1)
rownames(mse)[nrow(mse)] <- "PLS"
mse

##                  Min.    1st Qu.       Median         Mean   3rd Qu.     Max.
## OLS         -2.848756 -0.7345743 -0.063600785 -0.008475534 0.7779656 3.123769
## Forward     -2.694752 -0.6807069 -0.066485330 -0.008589938 0.6807813 2.933698
## Backward    -2.811408 -0.6704336 -0.006818937  0.002312087 0.7294619 2.556570
## Best subset -3.222127 -0.6878269 -0.092767711 -0.011493783 0.6494942 2.645342
## Ridge       -2.831095 -0.7317479 -0.069166253 -0.008504460 0.7913391 3.136069
## PCR         -3.001682 -0.7495731 -0.003277450 -0.029553171 0.6997885 2.625501
## PLS         -2.811643 -0.6771610 -0.074105470 -0.018173481 0.6729206 2.912326
##             MeanSqErr
## OLS          1.222308
## Forward      1.126742
## Backward     1.024182
## Best subset  1.064705
## Ridge        1.218283
## PCR          1.121846
## PLS          1.137367

PLS riduce a 2 il numero di feature (variabili indipendenti) nel modello. I risultati predittivi sono abbastanza buoni, anche se l’errore (Mean Squares Error) si posiziona tra quello dello stepwise e del PCR.

19.9 Elastic-Net

glmnet è un package che adatta modelli lineari generalizzati tramite massima verosimiglianza penalizzata. Il percorso di regolarizzazione per il parametro di regolarizzazione è calcolato su una griglia di valori. L’algoritmo è estremamente rapido, e può anche sfruttare la sparsità nella matrice di input $X$. glmnet adatta modelli di regressione lineari, logistici e multinomiali, di Poisson e di Cox.

L’approccio dell’elastic net (nel modello lineare) cerca di minimizzare la seguente funzione criterio: \[\frac{\sum_{i=1}^n \left(y_i - \underline{x}_i^T\underline{\beta} \right)^2}{n} + \lambda \sum_{j=1}^p \left[\alpha | \beta_j| +(1-\alpha) \beta_j^2 \right]\]

Dove $\underline{\beta}=(\beta_0, \beta_1, \cdots, \beta_p)^T$, (con $\beta_0$ l’intercetta), $0 \le \alpha \le1$, e $\lambda$ è il termine di penalizzazione.
Le variabili indipendenti (feature) sono usualmente standardizzate.

Quando $\alpha=1$, viene usato il cosiddetto termine di penalizzazione LASSO (Least Absolute Shrinkage and Selection Operator), che si basa sulla norma $L_1$.
L’uso della penalizzazione $L_1$, per un valore sufficientemente grande del parametro di tuning $\lambda$, porta ad una soluzione ceontenente un sottoinsieme di coefficienti $\beta_j$ esattamente pari a zero.

Quando $\alpha=0$, allora il problema sopra diveta un modello di regressione con termine di penalizzazione ridge, cioè basato sulla norma $L_2$.
La penalizzazione ridge, come già visto, tende a “costringere” o “restringere” i coefficienti delle variabili correlate a valori più prossimi a zero, e quindi più simili tra loro.

Elastic-net è stao introdotto come un compromesso tra queste due tecniche, ed adotta una penalizzazione che è un mix delle norme $L_1$ e $L_2$. Nel package, $\lambda$ può essere stimato tramite cross-validation, mentre (attualmente) $\alpha$ è impostato dall’utente.

library(glmnet)

# Impostato per riproducibilità
set.seed(10)

Cerchiamo dapprima un “buon” valore per lambda:

# Imposta il parametro di folding
foldid <- sample(rep(seq(10),length=nrow(dt_train)))
cv <- cv.glmnet(x = as.matrix(dt_train[, 1:100]),
                y = dt_train$y, alpha = 0.9, foldid=foldid)
plot(cv)

Il grafico mostra che un buon parametro lambda nel modello sarà compreso tra 0.0382617 (il valore che minimizza il mean-squares) e 0.1282379 (il valore che ottiene il valore di mean-square + 1 volta la deviazione standard di cross-validation).

Proviamo quindi a stimare il modello elastic-net usando il valore di lambda che minimizza il valore di mean-squares

glmnet_fit <- glmnet(x = as.matrix(dt_train[, 1:100]),
                     y = dt_train$y, lambda = cv$lambda.min, alpha = 0.9) 
coef(glmnet_fit)

## 101 x 1 sparse Matrix of class "dgCMatrix"
##                       s0
## (Intercept)  4.133463222
## x1           0.350337622
## x2           0.242805786
## x3          -1.079615665
## x4           0.229698173
## x5           .          
## x6           0.174820923
## x7           .          
## x8          -0.010753724
## x9           .          
## x10          .          
## x11          .          
## x12         -0.019337597
## x13          0.104843651
## x14          .          
## x15          0.019778392
## x16          .          
## x17          0.043943307
## x18          .          
## x19          .          
## x20          .          
## x21          .          
## x22          .          
## x23          .          
## x24          .          
## x25          .          
## x26         -0.086050839
## x27          .          
## x28          .          
## x29         -0.140569561
## x30          .          
## x31          .          
## x32          0.163607144
## x33          .          
## x34          0.259852203
## x35          .          
## x36          .          
## x37          .          
## x38         -0.009023136
## x39          .          
## x40          .          
## x41          .          
## x42          0.156652859
## x43         -0.136251593
## x44         -0.098907148
## x45          .          
## x46          .          
## x47          0.019166151
## x48          .          
## x49         -0.013214783
## x50         -0.023912645
## x51         -0.156150657
## x52          .          
## x53          .          
## x54          .          
## x55          .          
## x56         -0.060200653
## x57          .          
## x58         -0.024772338
## x59         -0.377653733
## x60          .          
## x61          .          
## x62          0.041341801
## x63          .          
## x64          .          
## x65          .          
## x66          .          
## x67          .          
## x68          .          
## x69          0.089342700
## x70          .          
## x71          .          
## x72          .          
## x73         -0.087334897
## x74          0.105189853
## x75          0.080349373
## x76         -0.066438484
## x77          0.078609064
## x78          .          
## x79         -0.054990037
## x80          .          
## x81         -0.028917199
## x82          0.109747388
## x83          .          
## x84          .          
## x85          .          
## x86          0.130323959
## x87          0.022176952
## x88         -0.079729784
## x89          .          
## x90          .          
## x91          .          
## x92          0.080784550
## x93          0.035575741
## x94          0.069153723
## x95          .          
## x96          .          
## x97          .          
## x98          .          
## x99         -0.010173756
## x100        -0.024203945

y_pred_glmnet <- as.numeric(predict(glmnet_fit, newx = as.matrix(dt_test[, 1:100])))
res <- dt_test$y - y_pred_glmnet
mse1 <- setNames(c(summary(res), mean(res^2)),
                 nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
mse <- rbind(mse, mse1)
rownames(mse)[nrow(mse)] <- "glmnet"
mse

##                  Min.    1st Qu.       Median         Mean   3rd Qu.     Max.
## OLS         -2.848756 -0.7345743 -0.063600785 -0.008475534 0.7779656 3.123769
## Forward     -2.694752 -0.6807069 -0.066485330 -0.008589938 0.6807813 2.933698
## Backward    -2.811408 -0.6704336 -0.006818937  0.002312087 0.7294619 2.556570
## Best subset -3.222127 -0.6878269 -0.092767711 -0.011493783 0.6494942 2.645342
## Ridge       -2.831095 -0.7317479 -0.069166253 -0.008504460 0.7913391 3.136069
## PCR         -3.001682 -0.7495731 -0.003277450 -0.029553171 0.6997885 2.625501
## PLS         -2.811643 -0.6771610 -0.074105470 -0.018173481 0.6729206 2.912326
## glmnet      -3.045912 -0.6644882 -0.019250860 -0.014396276 0.7298526 2.663014
##             MeanSqErr
## OLS          1.222308
## Forward      1.126742
## Backward     1.024182
## Best subset  1.064705
## Ridge        1.218283
## PCR          1.121846
## PLS          1.137367
## glmnet       1.072643

Si noti l’uso di cv$lambda.min per avere il valore di lambda per cui si minimizza l’errore CV.

Se vogliamo vedere cosa accade variando il valore del parametro lambda, possiamo usare il metodo plot()

glmnet_fit <- glmnet(x = as.matrix(dt_train[, 1:100]),
                     y = dt_train$y, alpha=1) # alpha di default (LASSO)
plot(glmnet_fit,xvar="lambda")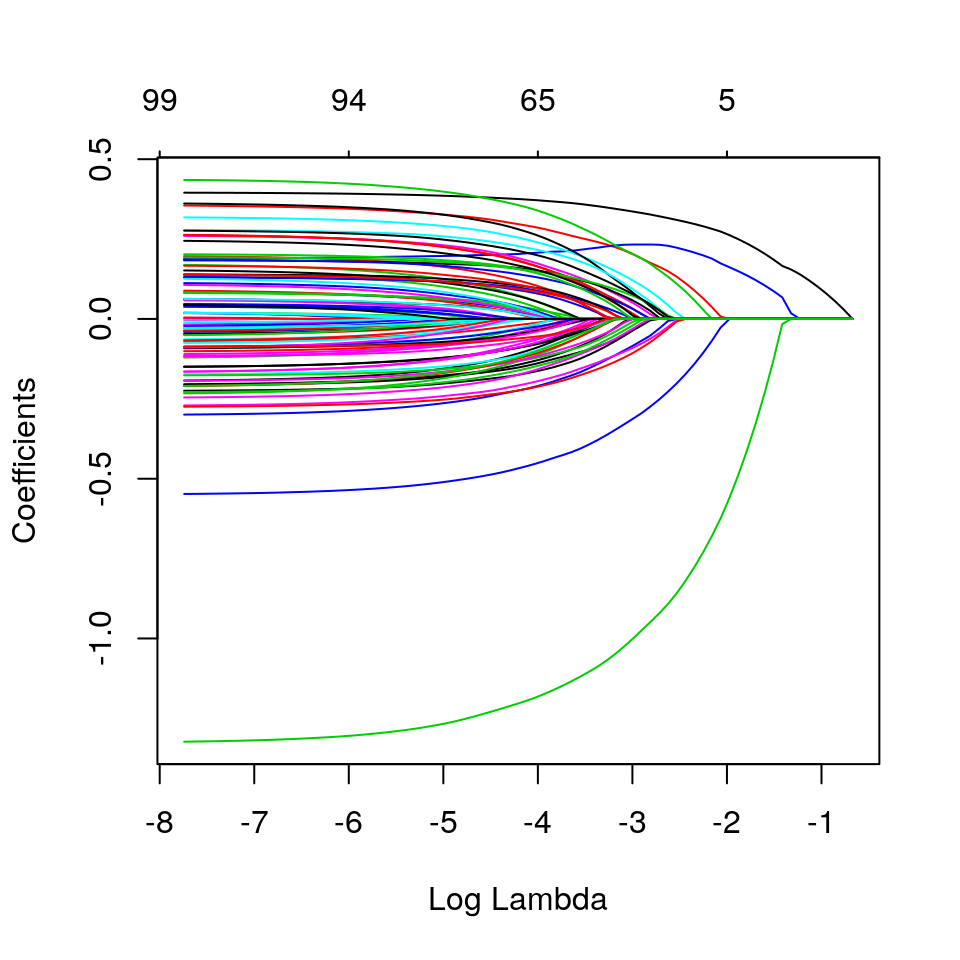

glmnet_fit <- glmnet(x = as.matrix(dt_train[, 1:100]),
                     y = dt_train$y, alpha=0.9) # elastic-net con alpha = 0.9
plot(glmnet_fit,xvar="lambda")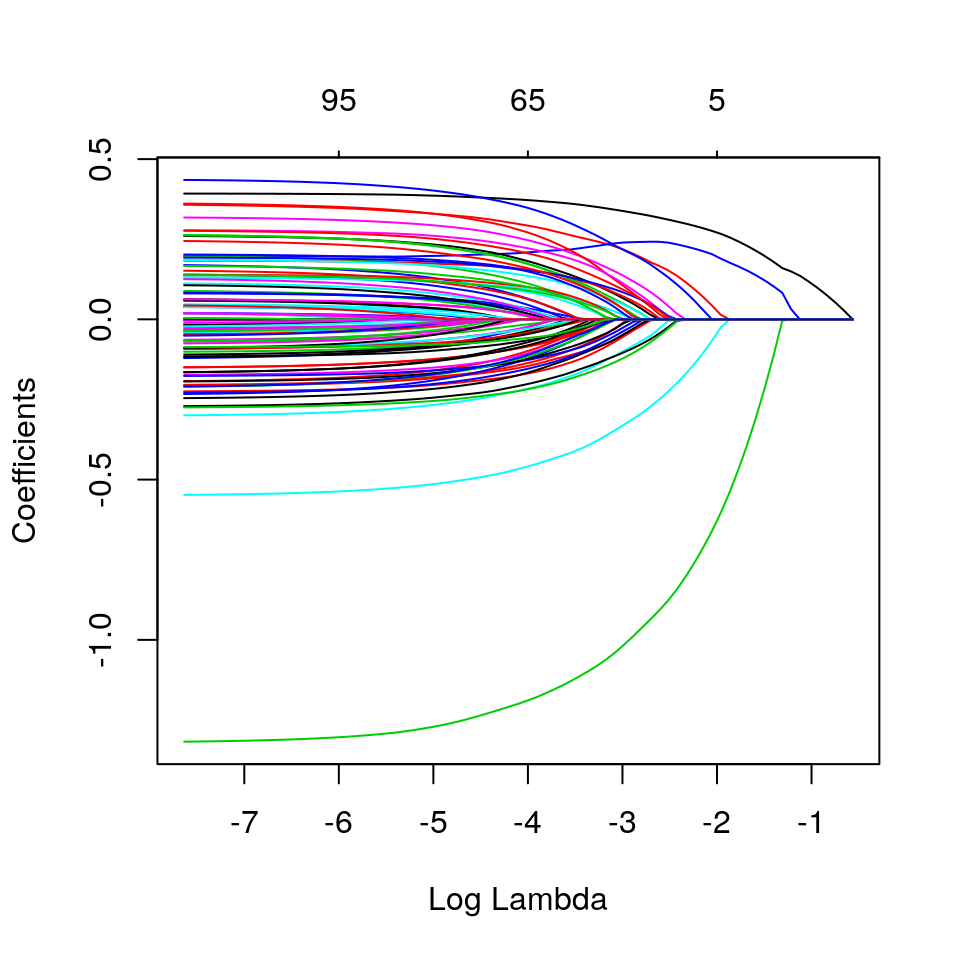

glmnet_fit <- glmnet(x = as.matrix(dt_train[, 1:100]),
                     y = dt_train$y, alpha=0) # ridge
plot(glmnet_fit,xvar="lambda")

Proveremo ora altre coombinazioni di lambda e alpha. Proveremo anche il valore di lambda.1se ottenuto dalla CV:

glmnet_fit <- glmnet(x = as.matrix(dt_train[, 1:100]),
                     y = dt_train$y, lambda = cv$lambda.1se, alpha = 0.9)
y_pred_glmnet <- as.numeric(predict(glmnet_fit, newx = as.matrix(dt_test[, 1:100])))
summary((y_pred_glmnet - dt_test$y)^2)

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
##  0.000019  0.138853  0.552895  1.129163  1.481501 12.210913

Qui cerchiamo il miglior valore di lambda, fissato alpha = 1:

cv <- cv.glmnet(x = as.matrix(dt_train[, 1:100]), y = dt_train$y, alpha = 1)
plot(cv)

Il grafico mostra che il parametro lambda è compreso tra 0.0377929 (il valore che minimizza il mean-squares) e 0.1154141 (il valore che ottiene il valore di mean-square + 1 volta la deviazione standard di cross-validation).

# Traccia i parametri del modello con alpha=0 (ridge), variando il valore del parametro della norma L1
glmnet_fit <- glmnet(x = as.matrix(dt_train[, 1:100]), y = dt_train$y, alpha = 0)
plot(glmnet_fit, label = TRUE)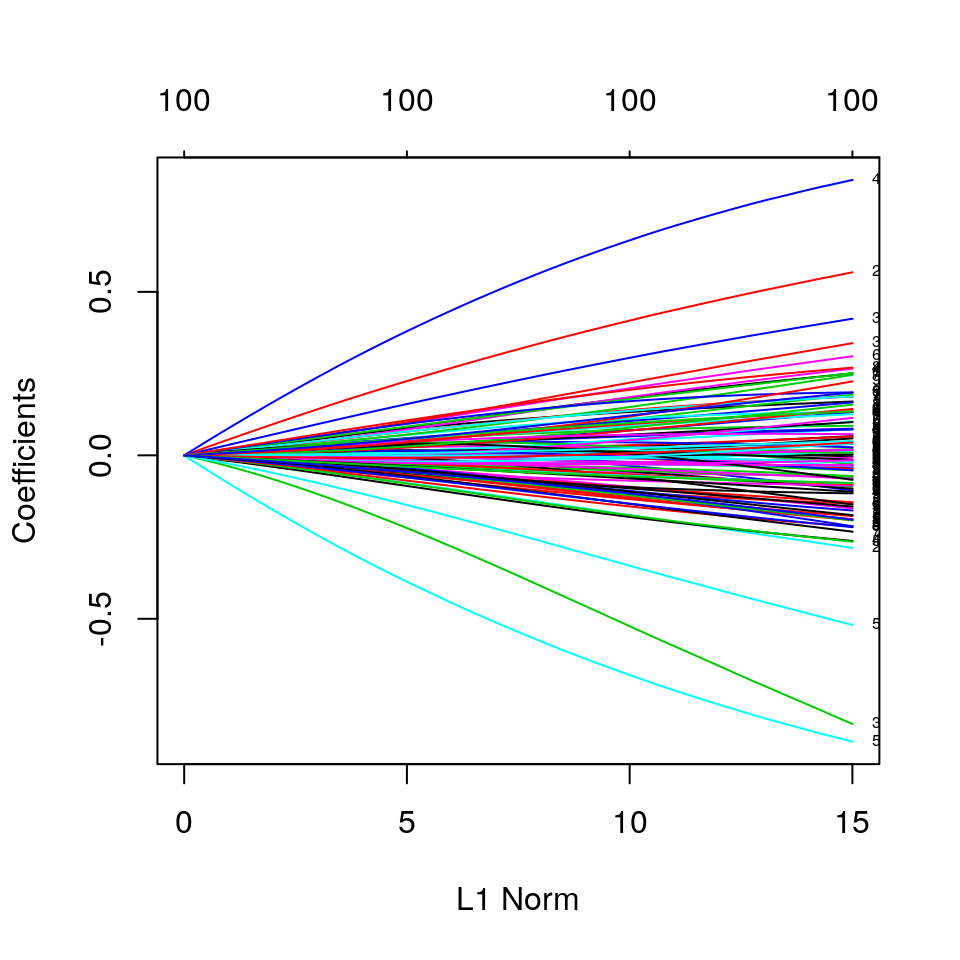

# Confronta i modelli con alpha=1 (LASSO) con lambda.min e lambda.1se
glmnet_fit <- glmnet(x = as.matrix(dt_train[, 1:100]),
                     y = dt_train$y, lambda = cv$lambda.min, alpha = 1)
y_pred_glmnet <- as.numeric(predict(glmnet_fit, newx = as.matrix(dt_test[, 1:100])))
summary((y_pred_glmnet - dt_test$y)^2)

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## 0.000018 0.086626 0.447190 1.070987 1.453859 9.501180

glmnet_fit <- glmnet(x = as.matrix(dt_train[, 1:100]),
                     y = dt_train$y, lambda = cv$lambda.1se, alpha = 1)
y_pred_glmnet <- as.numeric(predict(glmnet_fit, newx = as.matrix(dt_test[, 1:100])))
summary((y_pred_glmnet - dt_test$y)^2)

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
##  0.00001  0.13972  0.54427  1.12663  1.49316 12.11803

I risultati per alpha = 0.9 e alpha = 1 sono sostanzialmente confrontabili. L’uso di lambda.min o lambda.1se non sembra modificare sensibilmente i risultati. In ogni modo, sembra che la migliore soluzione sia la LASSO.

Ora proveremo ad eseguire una ricerca su griglia della coppia dei parametri (lambda, alpha) che produce il miglior modello:

alphas <- (0:101)/101
cv_fits <- lapply(X = alphas,FUN = function(a, dt_train, foldid){
      fit <- cv.glmnet(x = as.matrix(dt_train[, 1:100]),
                       y = dt_train$y, alpha = a, foldid = foldid)
      return(fit)
    },
    dt_train=dt_train, foldid=foldid
  )

mins <- t(sapply(X = cv_fits,
                 FUN = function(x){return(c(lambda=x$lambda.min, cvm=min(x$cvm, na.rm = TRUE) ))}))
wm <- which.min(mins[,"cvm"])
alpha_opt <- alphas[wm]
(opt <- c(alpha=alpha_opt, mins[wm,]))

##     alpha    lambda       cvm 
## 1.0000000 0.0344355 1.0232540

glmnet_fit <- glmnet(x = as.matrix(dt_train[, 1:100]),
                     y = dt_train$y, lambda = opt["lambda"], alpha = opt["alpha"])
coef(glmnet_fit, label = TRUE)

## 101 x 1 sparse Matrix of class "dgCMatrix"
##                       s0
## (Intercept)  4.138194173
## x1           0.352820394
## x2           0.240728302
## x3          -1.087953796
## x4           0.223343743
## x5           .          
## x6           0.175639210
## x7           .          
## x8          -0.010753877
## x9           .          
## x10          .          
## x11          .          
## x12         -0.020008885
## x13          0.105606683
## x14          .          
## x15          0.020182371
## x16          .          
## x17          0.044020621
## x18          .          
## x19          .          
## x20          .          
## x21          .          
## x22          .          
## x23          .          
## x24          .          
## x25          .          
## x26         -0.086724372
## x27          .          
## x28          .          
## x29         -0.141554033
## x30          .          
## x31          .          
## x32          0.164358825
## x33          .          
## x34          0.260658504
## x35          .          
## x36          .          
## x37          .          
## x38         -0.008811135
## x39          .          
## x40          .          
## x41          .          
## x42          0.157467889
## x43         -0.136392485
## x44         -0.099425366
## x45          .          
## x46          .          
## x47          0.019587234
## x48          .          
## x49         -0.013070072
## x50         -0.023536291
## x51         -0.157012097
## x52          .          
## x53          .          
## x54          .          
## x55          .          
## x56         -0.060307977
## x57          .          
## x58         -0.025288824
## x59         -0.379043697
## x60          .          
## x61          .          
## x62          0.042062459
## x63          .          
## x64          .          
## x65          .          
## x66          .          
## x67          .          
## x68          .          
## x69          0.089114134
## x70          .          
## x71          .          
## x72          .          
## x73         -0.087977809
## x74          0.105771820
## x75          0.081052766
## x76         -0.066878180
## x77          0.078231791
## x78          .          
## x79         -0.055460865
## x80          .          
## x81         -0.028652557
## x82          0.109652931
## x83          .          
## x84          .          
## x85          .          
## x86          0.130745915
## x87          0.022375403
## x88         -0.080033798
## x89          .          
## x90          .          
## x91          .          
## x92          0.081913488
## x93          0.035932709
## x94          0.069806834
## x95          .          
## x96          .          
## x97          .          
## x98          .          
## x99         -0.010041306
## x100        -0.024389679

y_pred_glmnet <- as.numeric(predict(glmnet_fit, newx = as.matrix(dt_test[, 1:100])))

res <- dt_test$y - y_pred_glmnet
mse1 <- setNames(c(summary(res), mean(res^2)),
                 nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
mse <- rbind(mse, mse1)
rownames(mse)[nrow(mse)] <- "best-glmnet"
mse

##                  Min.    1st Qu.       Median         Mean   3rd Qu.     Max.
## OLS         -2.848756 -0.7345743 -0.063600785 -0.008475534 0.7779656 3.123769
## Forward     -2.694752 -0.6807069 -0.066485330 -0.008589938 0.6807813 2.933698
## Backward    -2.811408 -0.6704336 -0.006818937  0.002312087 0.7294619 2.556570
## Best subset -3.222127 -0.6878269 -0.092767711 -0.011493783 0.6494942 2.645342
## Ridge       -2.831095 -0.7317479 -0.069166253 -0.008504460 0.7913391 3.136069
## PCR         -3.001682 -0.7495731 -0.003277450 -0.029553171 0.6997885 2.625501
## PLS         -2.811643 -0.6771610 -0.074105470 -0.018173481 0.6729206 2.912326
## glmnet      -3.045912 -0.6644882 -0.019250860 -0.014396276 0.7298526 2.663014
## best-glmnet -3.039856 -0.6642515 -0.017604178 -0.014375195 0.7284476 2.660265
##             MeanSqErr
## OLS          1.222308
## Forward      1.126742
## Backward     1.024182
## Best subset  1.064705
## Ridge        1.218283
## PCR          1.121846
## PLS          1.137367
## glmnet       1.072643
## best-glmnet  1.072511

Sorprendentemente, il miglior modello trovato non è effettivamente “il migliore”. Ciò potrebbe essere dovuto a molte cause, tra cui effetti di arrotondamento. In ogni modo, le differenze tra questo modello ed il precedente sono veramente molto piccole.

19.10 Lasso e Post-Lasso

Il package R hdm contiene implementazioni di metodi sviluppati di recente per modelli ad elevata dimensnionalità approssimativamente sparsi, basati principalmente su metodi Lasso e Post-Lasso. Questo package è utilizzabile quando il numero di parametri da stimare ($p$) è più grande della dimensione campionaria ($n$) ma si ipotizza che solo una frazione relativamente piccola $s = o(n)$ dei predittori sia importante per catturare accuratamente le caratteristiche principali della funzione di regressione.

library(hdm)

Lo stimatore Lasso è un caso particolare dell’Elastic-Net, dove $\alpha = 1$. Lo stimatore si basa sulla norma $L_1$, che permette di evitare l’overfitting, ma che può anche “sospingere” i coefficienti stimati verso lo zero, causando una distorsione potenzialmente importante. Per rimuovere parte di questa distorsione, si considera il Post-Lasso, che è uno stimatore definito sostanzialmente come l’applicazione dei minimi quadrati ordinari applicati ai dati dopo aver rimosso i regressori non selezionati dal Lasso.

La funzione rlasso() del package hdm implementa Lasso e post-Lasso. Il prefisso “r” indica che queste sono versioni teoricamente rigorosse di Lasso e post-Lasso. L’opzione di default è la post-Lasso, post=TRUE. Questa funzione ritorna un oggetto di classe rlasso per cui sono forniti metodi quali predict, print, summary, e dove è presente un’opzione all, impostabile a FALSE, per non limitare la stampa dei soli coefficienti diversi da zero.

Vediamo ora come “si comporta” il metodo Post-Lasso:

post_lasso_reg <- rlasso(x = dt_train[,1:100], y = dt_train$y, post = TRUE) 
summary(post_lasso_reg, all = FALSE)

## 
## Call:
## rlasso.default(x = dt_train[, 1:100], y = dt_train$y, post = TRUE)
## 
## Post-Lasso Estimation:  TRUE 
## 
## Total number of variables: 100
## Number of selected variables: 3 
## 
## Residuals: 
##      Min       1Q   Median       3Q      Max 
## -3.43055 -0.63210 -0.04239  0.67393  3.22206 
## 
##             Estimate
## (Intercept)    4.424
## x1             0.391
## x3            -1.287
## x4             0.288
## 
## Residual standard error: 1.008
## Multiple R-squared:  0.2842
## Adjusted R-squared:  0.2813
## Joint significance test:
##  the sup score statistic for joint significance test is 21.91 with a p-value of     0

Il modello sui dati di training non sembra selezionare correttamente tutte le variabili che effettivamente impattano sulla variabile dipendente, e quasi tutti i parametri sono un po’ distanti dai veri valori dei parametri. Questo potrebbe dipendenre dalla alta multicollinearità.

Vediamo ora le performance predittive:

y_pred_post_lasso <- c(predict(post_lasso_reg, newdata = dt_test)) 

ggp <- ggplot(data = data.frame(fit=y_pred_post_lasso, obs=dt_test$y),
              mapping = aes(x = obs, y = fit)) +
  geom_point() +
  ggtitle("Post-Lasso: Osservati Vs. Previsti") +
  xlab("Y osservati") + ylab("Y previsti") + 
  geom_abline(slope = 1,intercept = 0, colour="red")
print(ggp)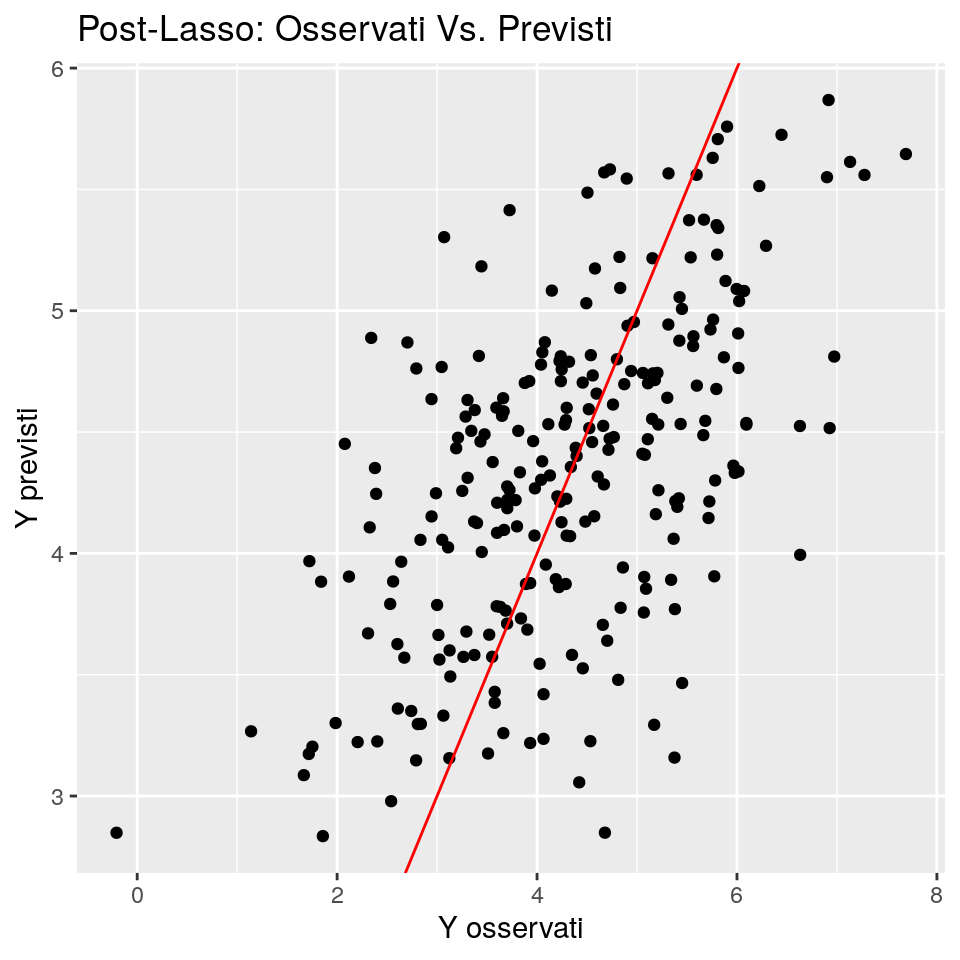

res <- dt_test$y - y_pred_post_lasso
mse1 <- setNames(c(summary(res), mean(res^2)),
                 nm = c("Min.","1st Qu.","Median","Mean","3rd Qu.","Max.","MeanSqErr"))
mse <- rbind(mse, mse1)
rownames(mse)[nrow(mse)] <- "Post-Lasso"
mse

##                  Min.    1st Qu.       Median         Mean   3rd Qu.     Max.
## OLS         -2.848756 -0.7345743 -0.063600785 -0.008475534 0.7779656 3.123769
## Forward     -2.694752 -0.6807069 -0.066485330 -0.008589938 0.6807813 2.933698
## Backward    -2.811408 -0.6704336 -0.006818937  0.002312087 0.7294619 2.556570
## Best subset -3.222127 -0.6878269 -0.092767711 -0.011493783 0.6494942 2.645342
## Ridge       -2.831095 -0.7317479 -0.069166253 -0.008504460 0.7913391 3.136069
## PCR         -3.001682 -0.7495731 -0.003277450 -0.029553171 0.6997885 2.625501
## PLS         -2.811643 -0.6771610 -0.074105470 -0.018173481 0.6729206 2.912326
## glmnet      -3.045912 -0.6644882 -0.019250860 -0.014396276 0.7298526 2.663014
## best-glmnet -3.039856 -0.6642515 -0.017604178 -0.014375195 0.7284476 2.660265
## Post-Lasso  -3.055326 -0.7354125 -0.020493580 -0.024752001 0.6792215 2.638292
##             MeanSqErr
## OLS          1.222308
## Forward      1.126742
## Backward     1.024182
## Best subset  1.064705
## Ridge        1.218283
## PCR          1.121846
## PLS          1.137367
## glmnet       1.072643
## best-glmnet  1.072511
## Post-Lasso   1.062298

I risultati predittivi sono comunque buoni e piuttosto prossimi a quelli di glmnet.