Capitolo 18 Richiami sul modello lineare (LM)

require(ggplot2)
require(pdataita)

18.1 Esempio: Regressione per effetto tranquillante su topi

18.1.1 Descrizione dei dati

In un esperimento in cui si investiga l’effetto di un tranquillante, sono misurati i tempi di reazione ad uno stimolo di topi dopo che a ciascuno di questi è stato somministrata una dose diversa del farmaco.

18.1.2 Caricamento dei dati

data(drug)
str(drug)

## Classes 'tbl_df', 'tbl' and 'data.frame':    10 obs. of  3 variables:
##  $ rat : int  1 2 3 4 5 6 7 8 9 10
##  $ dose: num  0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
##  $ time: num  0.32 0.24 0.4 0.52 0.44 0.56 0.64 0.52 0.6 0.8

head(drug)

## # A tibble: 6 x 3
##     rat  dose  time
##   <int> <dbl> <dbl>
## 1     1   0    0.32
## 2     2   0.1  0.24
## 3     3   0.2  0.4 
## 4     4   0.3  0.52
## 5     5   0.4  0.44
## 6     6   0.5  0.56

18.1.3 Statistiche descrittive

Poiché siamo principalmente interessati alla relazione tra la dose del farmaco e i tempi di reazione (time), iniziamo una analisi descrittive tracciando un grafico che mette in relazione queste due variabili.

ggp <- ggplot(data=drug, mapping = aes(x=dose, y=time)) +
  geom_point(color="darkblue", size=2) +
  geom_smooth(method = "lm", colour="red", se = FALSE) +
  geom_smooth(method = "loess", colour="green", se = FALSE, span=1) +
  xlab("dose (mg)") + ylab("Tempo di reazione (sec)")
print(ggp)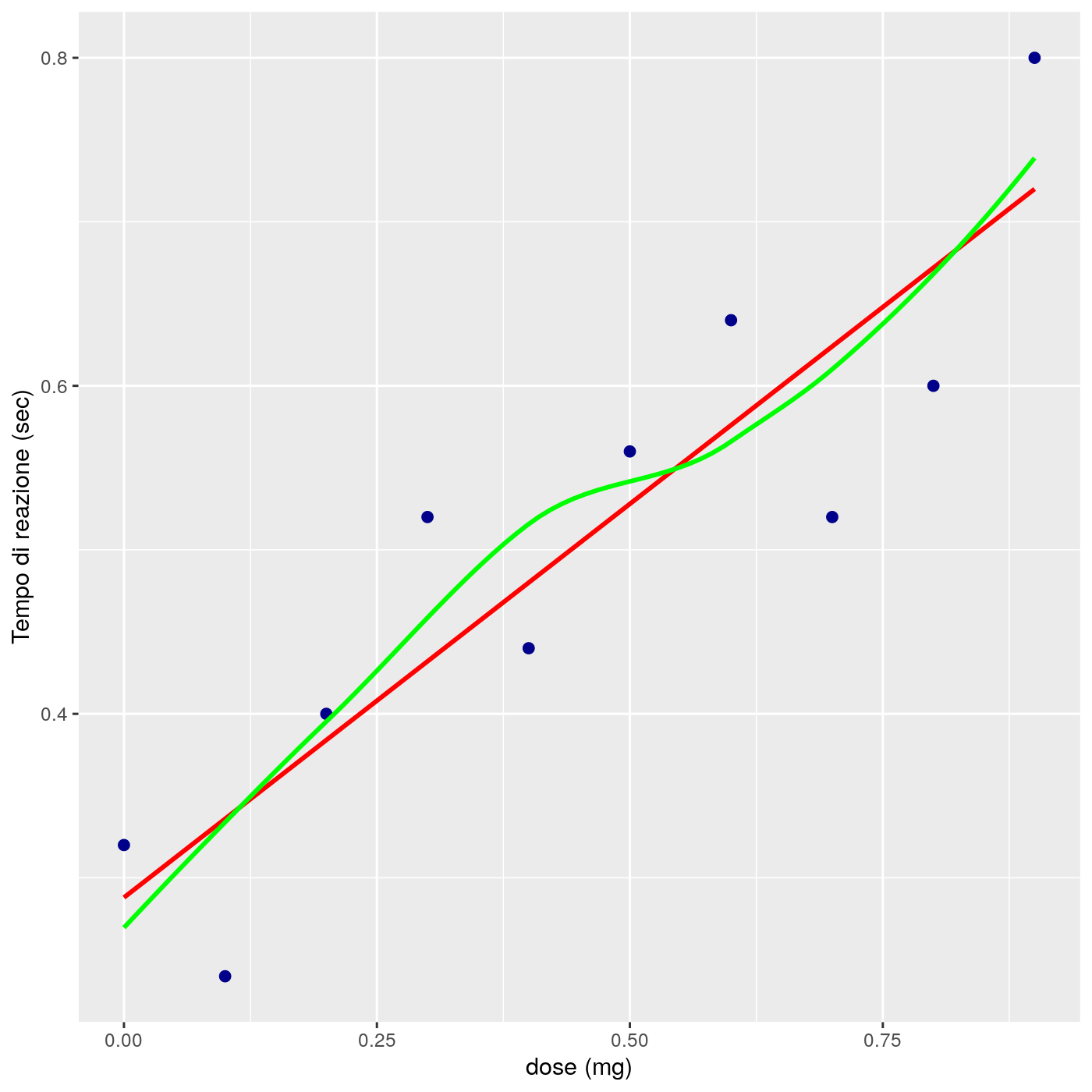

Figura 18.1: Scatterplot di tempo Vs. dose con regressione lineare e linea loess

Nel codice qui sopra, method="lm" della chiamata della funzione geom_smooth() aggiunge la retta di regressione all’oggetto ggp e method="loess" di geom_smooth() aggiunge una linea di regressione locale all’oggetto ggp.

Probabilmente una retta di regressione semplice è una buona scelta per descrivere la relazione.

18.1.4 Inferenza e modelli

Adattiamo quindi un semplice modello lineare \(E(y_i \vert xi) = \beta_0 + \beta_1 \cdot x_i\) tra il tempo di reazione e la dose del farmaco e produciamo un riepilogo del modello adattato.

fm <- lm(time ~ dose, data = drug)
summary(fm)

## 
## Call:
## lm(formula = time ~ dose, data = drug)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -0.104 -0.064  0.024  0.056  0.088 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.28800    0.04522   6.368 0.000216 ***
## dose         0.48000    0.08471   5.666 0.000472 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.07694 on 8 degrees of freedom
## Multiple R-squared:  0.8005, Adjusted R-squared:  0.7756 
## F-statistic: 32.11 on 1 and 8 DF,  p-value: 0.0004724

Leggendo i risultati, sembra che aumentando la dose di una unità, il tempo (time) cresce in media di 0.48, e questa crescita sia significativa.

Un altro modo per ottenere il p-value per il parametro di dose è confrontare il modello time ~ dose col modello time ~ 1, e testare quindi la significatività del coefficiente angolare tramite anova()

anova(fm,update(fm,.~.-dose))

## Analysis of Variance Table
## 
## Model 1: time ~ dose
## Model 2: time ~ 1
##   Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
## 1      8 0.04736                                  
## 2      9 0.23744 -1  -0.19008 32.108 0.0004724 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Il risultato è lo stesso.

18.1.5 Analisi dei residui

op <- par(mfrow = c(2, 2))
plot(fm)
par(op)

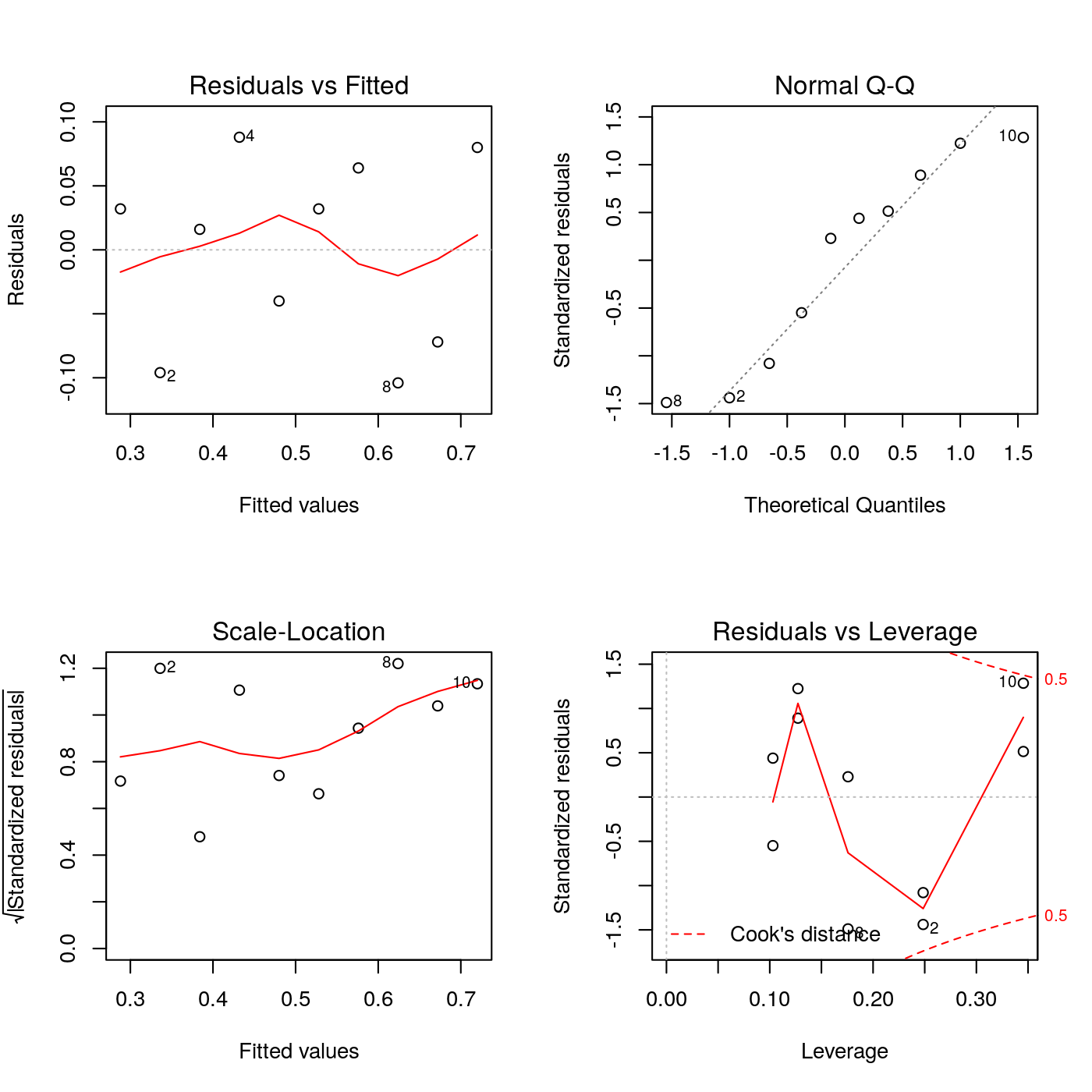
Figura 18.2: Grafico dei residui del modello lineare semplice

I grafici non evidenziano problemi particolari.

18.2 Esempio: Regressione su poliesterificazione

18.2.1 Descrizione dei dati

Nello studio della poliesterificazione degli acidi grassi con glicoli, è studiato l’effetto della temperatura (temperature \(^◦\)C) sulla percentuale di conversione del processo di esterificazione (conversion). I dati sono il risultato di un esperimento che usa un catalizzatore di \(4 \cdot 10^{−4}\) mole zinc chloride ogni 100 grammi di acidi grassi.

18.2.2 Caricamento dei dati

data(polyester)
str(polyester)

## Classes 'tbl_df', 'tbl' and 'data.frame':    6 obs. of  2 variables:
##  $ temperature: int  175 200 225 250 275 300
##  $ conversion : int  67 83 93 97 99 92

head(polyester)

## # A tibble: 6 x 2
##   temperature conversion
##         <int>      <int>
## 1         175         67
## 2         200         83
## 3         225         93
## 4         250         97
## 5         275         99
## 6         300         92

18.2.3 Statistiche descrittive

Rappresentiamo graficamente la relazione tra la variabile dipendente e la variabile indipendente.

ggp <- ggplot(data = polyester, mapping=aes(x = temperature, y=conversion)) +
  geom_point(color="darkblue") + xlab("temperatura   (°C)") +
  ylab("Percentuale di conversione (%)")

print(ggp)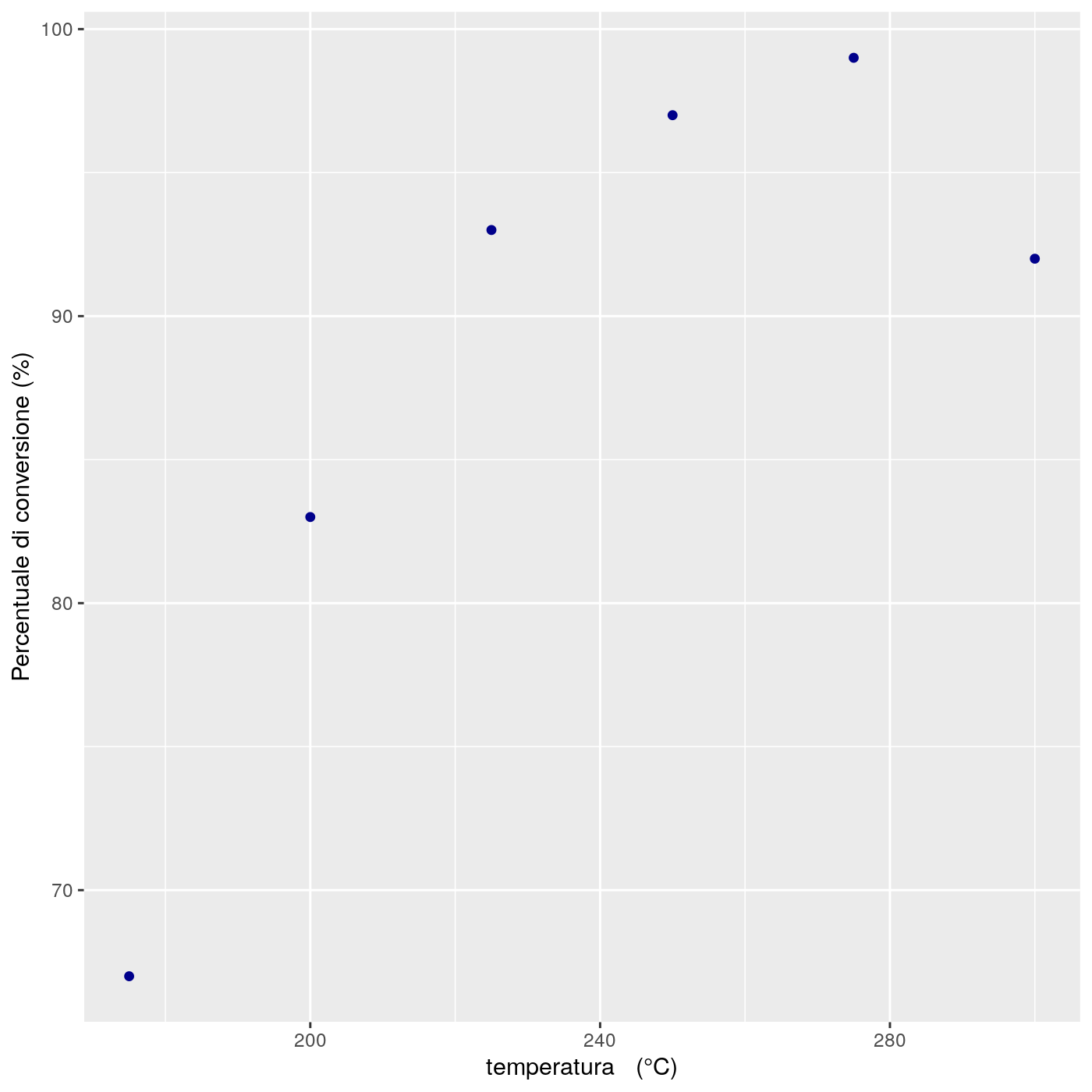

Figura 18.3: Scatterplot della conversione Vs. temperatura

Sembra che una funzione quadratica (una parabola) possa descrivere bene i dati.

18.2.4 Inferenza e modelli

A dispetto dell’evidenza qui sopra, proviamo inizialmente a stimare un modello lineare semplice, e produrre un grafico illustrativo del modello stesso.

fm0 <- lm(conversion ~ temperature, data = polyester) 
summary(fm0)

## 
## Call:
## lm(formula = conversion ~ temperature, data = polyester)
## 
## Residuals:
##      1      2      3      4      5      6 
## -8.857  2.086  7.029  5.971  2.914 -9.143 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept) 40.45714   18.60031   2.175   0.0953 .
## temperature  0.20229    0.07708   2.624   0.0585 .
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.061 on 4 degrees of freedom
## Multiple R-squared:  0.6326, Adjusted R-squared:  0.5407 
## F-statistic: 6.887 on 1 and 4 DF,  p-value: 0.05853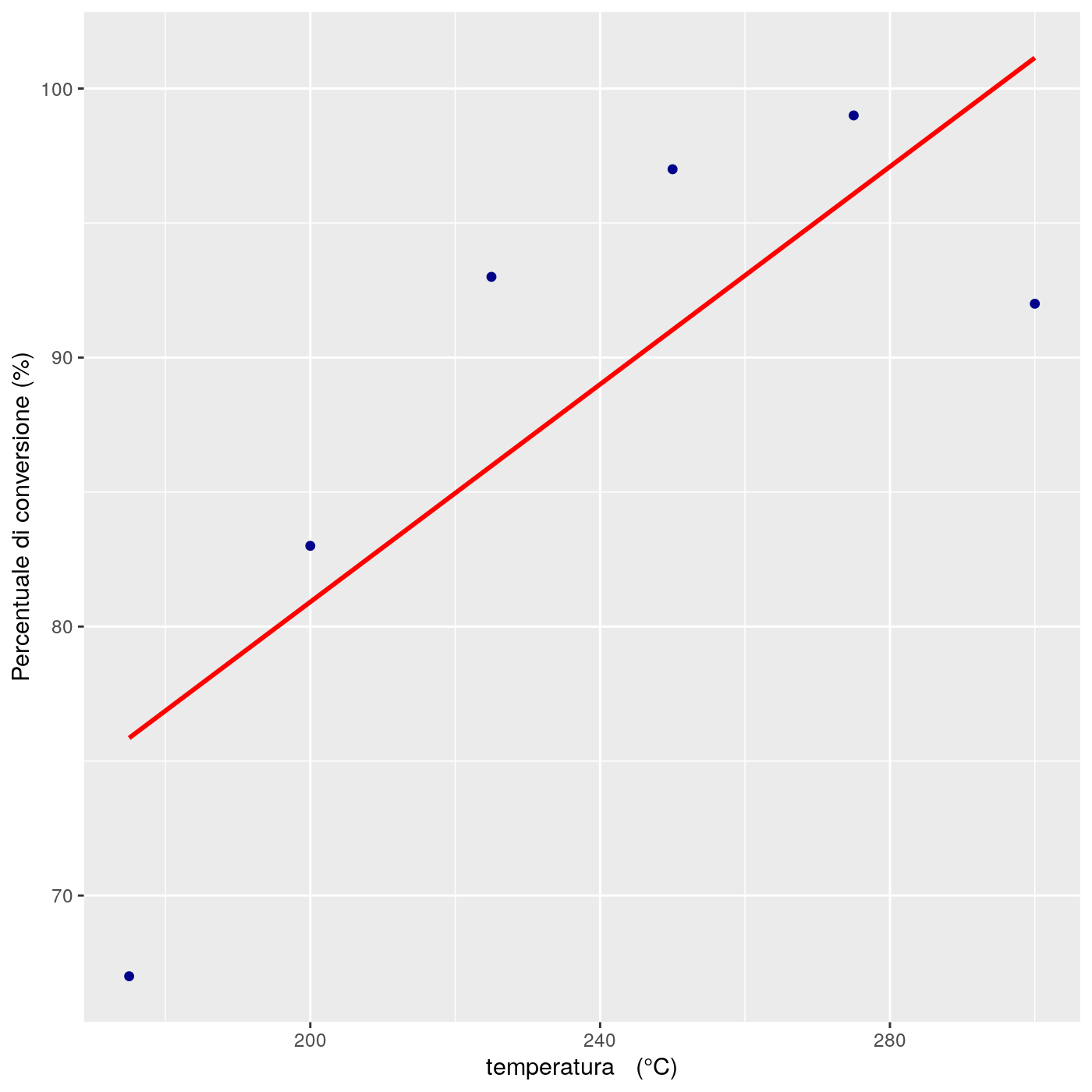

ggp0 <- ggp + geom_smooth(method = "lm", colour="red", se = FALSE)

print(ggp0)

Figura 18.4: Scatterplot di conversione Vs. temperatura con modello lineare

Ora il grafico dei residui.

op <- par(mfrow=c(2,2))
plot(fm0)
par(op)

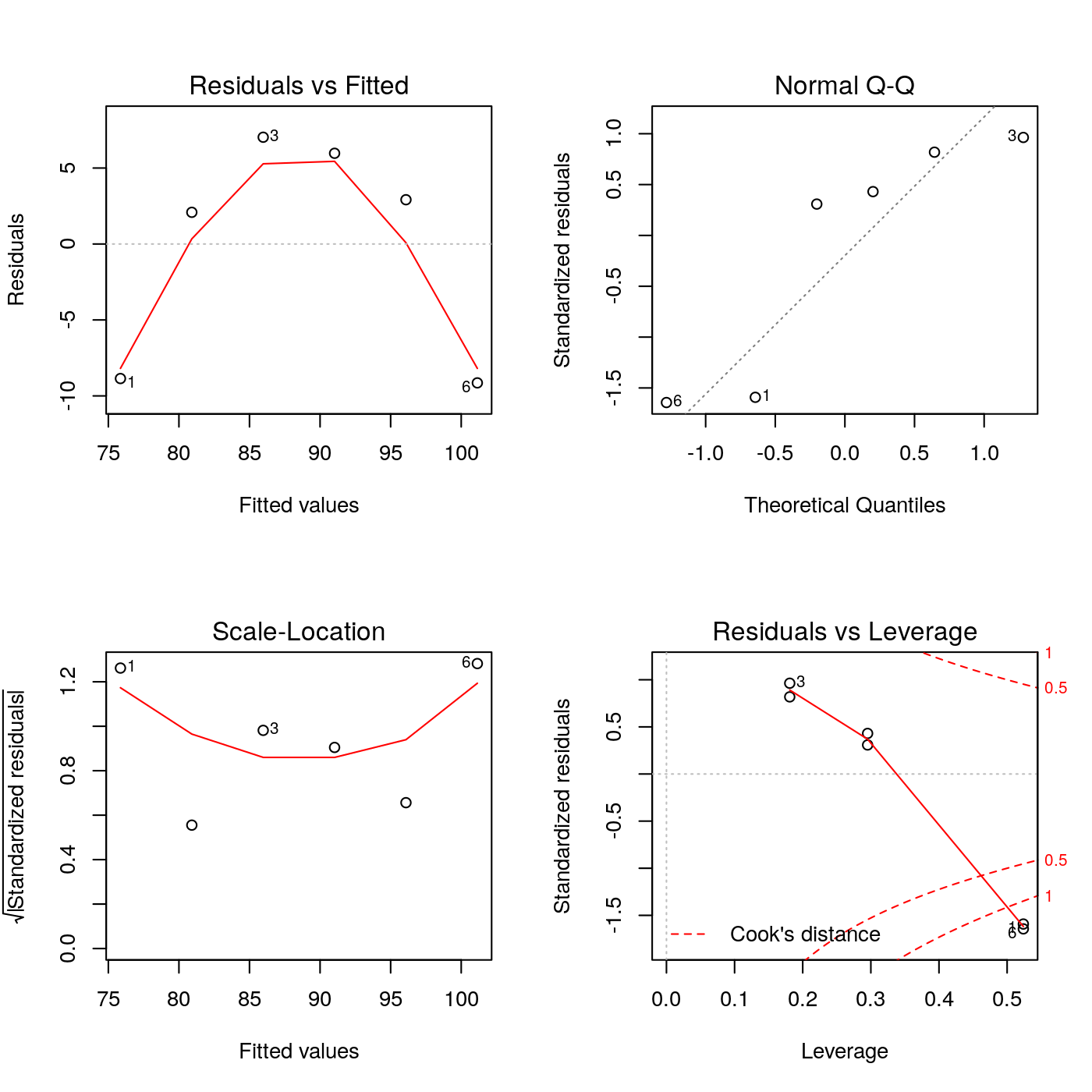
Figura 18.5: Analisi dei residui del modello lineare semplice conversione Vs. temperatura

Entrambi i grafici suggeriscono che potrebbe esistere un effetto di curvatura.
Un atro grafico per verificare questa ipotesi, è il grafico dei residui Vs. la variabile indiependente:

df <- data.frame(temperature = polyester$temperature, mod_residuals =residuals(fm0))

ggp <- ggplot(data = df, mapping = aes(x=temperature, y=mod_residuals)) +
  geom_point(color="darkblue") + geom_hline(yintercept = 0, colour="darkgreen")

print(ggp)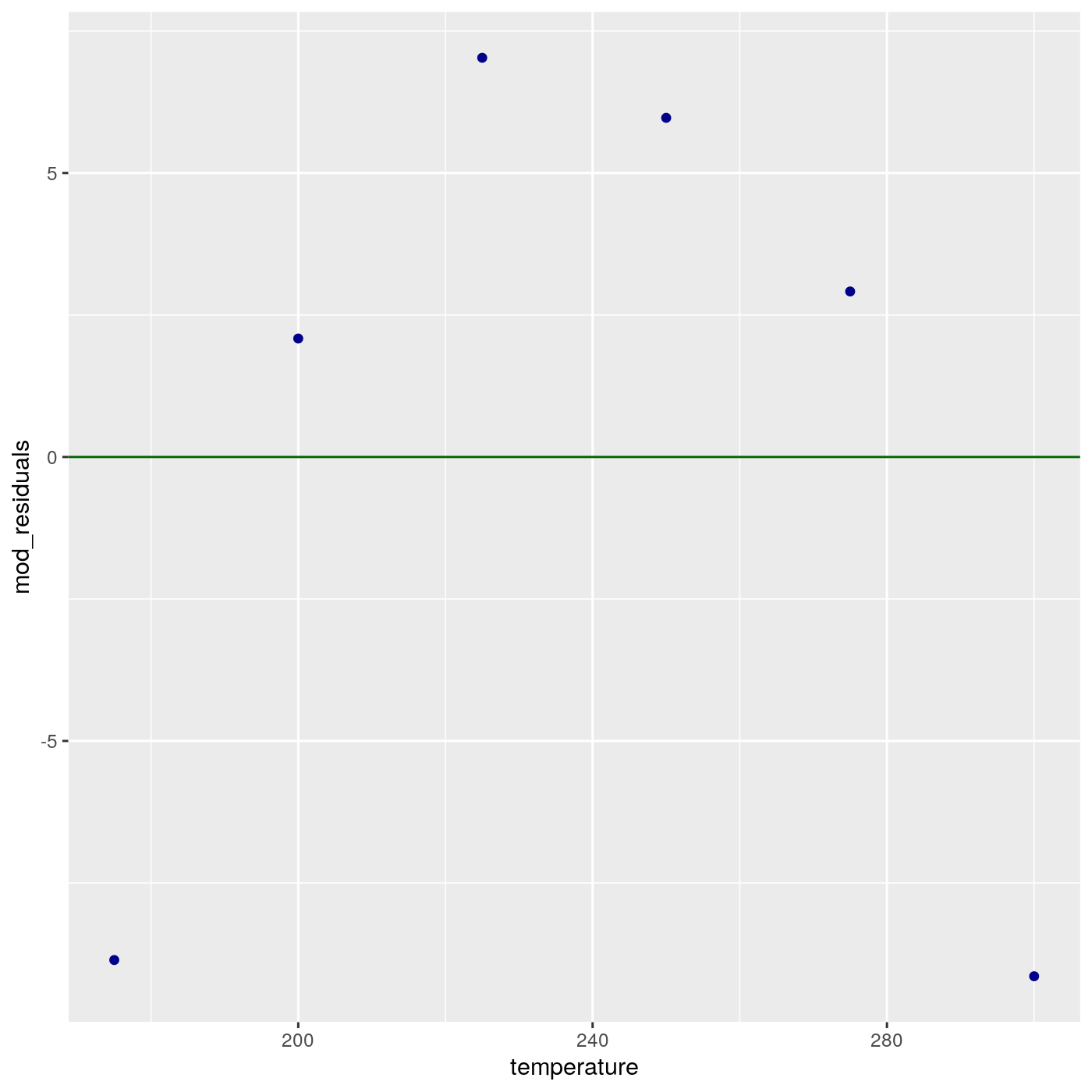

Figura 18.6: Scatterplot dei residui Vs. temperatura

Si nota una chiara curvatura.

A questo punto quindi possiamo provare un modello quadratico:

fm <- lm(conversion ~ poly(temperature, 2, raw = TRUE), data = polyester)

o, alternativamente:

fm <- update(fm0,.~. + I(temperature^2))

Oa guardiamo il riepilogo del modello

summary(fm)

## 
## Call:
## lm(formula = conversion ~ temperature + I(temperature^2), data = polyester)
## 
## Residuals:
##        1        2        3        4        5        6 
## -0.10714  0.33571  0.02857 -1.02857  1.16429 -0.39286 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      -1.888e+02  1.372e+01  -13.76 0.000830 ***
## temperature       2.197e+00  1.182e-01   18.59 0.000340 ***
## I(temperature^2) -4.200e-03  2.481e-04  -16.93 0.000449 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9474 on 3 degrees of freedom
## Multiple R-squared:  0.9962, Adjusted R-squared:  0.9937 
## F-statistic: 392.6 on 2 and 3 DF,  p-value: 0.0002348

Tutti i parametri sono significativi, e questo conferma l’osservazione iniziale di una relazione lineare.

18.2.5 Analisi dei residui

op <- par(mfrow=c(2,2))
plot(fm)
par(op)

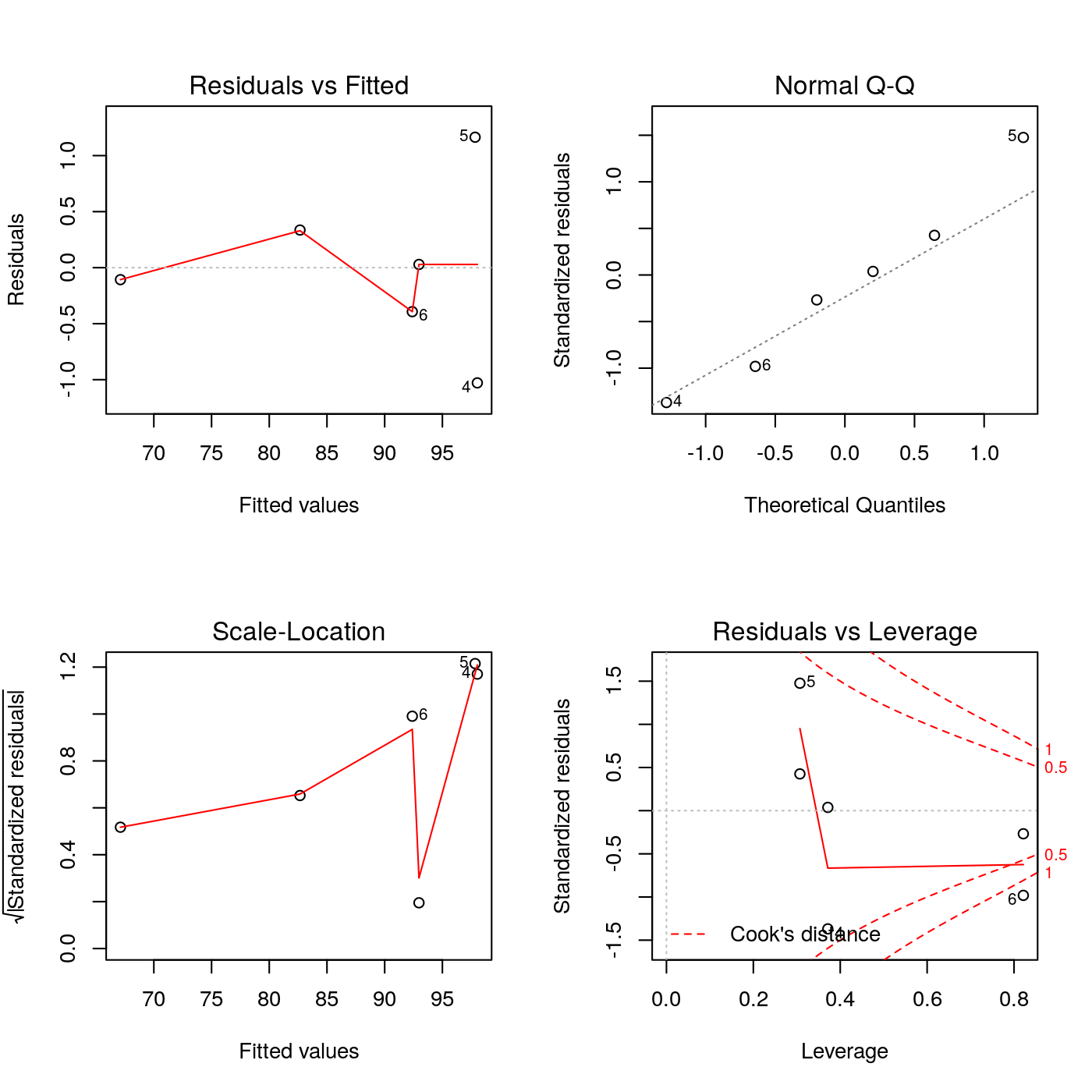
Figura 18.7: Grafico dei residui del modello finale

Il grafico dei residui sembra piuttosto “regolare”.

Come verifica aggiuntiva, possiamo provare anche l’agigunta di un termine cubico della temperatura.

(fm1 <- update(fm,.~. + I(temperature^3)))

## 
## Call:
## lm(formula = conversion ~ temperature + I(temperature^2) + I(temperature^3), 
##     data = polyester)
## 
## Coefficients:
##      (Intercept)       temperature  I(temperature^2)  I(temperature^3)  
##       -1.663e+02         1.902e+00        -2.933e-03        -1.778e-06

summary(fm1)

## 
## Call:
## lm(formula = conversion ~ temperature + I(temperature^2) + I(temperature^3), 
##     data = polyester)
## 
## Residuals:
##        1        2        3        4        5        6 
## -0.19048  0.45238  0.09524 -1.09524  1.04762 -0.30952 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)
## (Intercept)      -1.663e+02  1.168e+02  -1.424    0.290
## temperature       1.902e+00  1.524e+00   1.248    0.338
## I(temperature^2) -2.933e-03  6.519e-03  -0.450    0.697
## I(temperature^3) -1.778e-06  9.139e-06  -0.195    0.864
## 
## Residual standard error: 1.15 on 2 degrees of freedom
## Multiple R-squared:  0.9963, Adjusted R-squared:  0.9907 
## F-statistic: 177.8 on 3 and 2 DF,  p-value: 0.005598

anova(fm1,fm)

## Analysis of Variance Table
## 
## Model 1: conversion ~ temperature + I(temperature^2) + I(temperature^3)
## Model 2: conversion ~ temperature + I(temperature^2)
##   Res.Df    RSS Df Sum of Sq      F Pr(>F)
## 1      2 2.6429                           
## 2      3 2.6929 -1     -0.05 0.0378 0.8637

Questo modello cubico non aggiunge informazione utile rispetto al modello quadratico.
Ora, usiamo il modello quadratico per producce un grafico dei valori previsti:

newdata <- data.frame(temperature = seq(min(polyester$temperature), 
  max(max(polyester$temperature)), length = 100))
newdata$predict <- predict(fm, newdata = newdata)

ggp <- ggplot(data=polyester, mapping = aes(x=temperature, y=conversion)) +
  geom_point(colour="darkblue", size=3) + 
  geom_line(data=newdata, mapping=aes(x=temperature, y=predict), colour="mediumvioletred") + 
  xlab("temperatura (°C)") + ylab("conversione percentuale (%)")

print(ggp)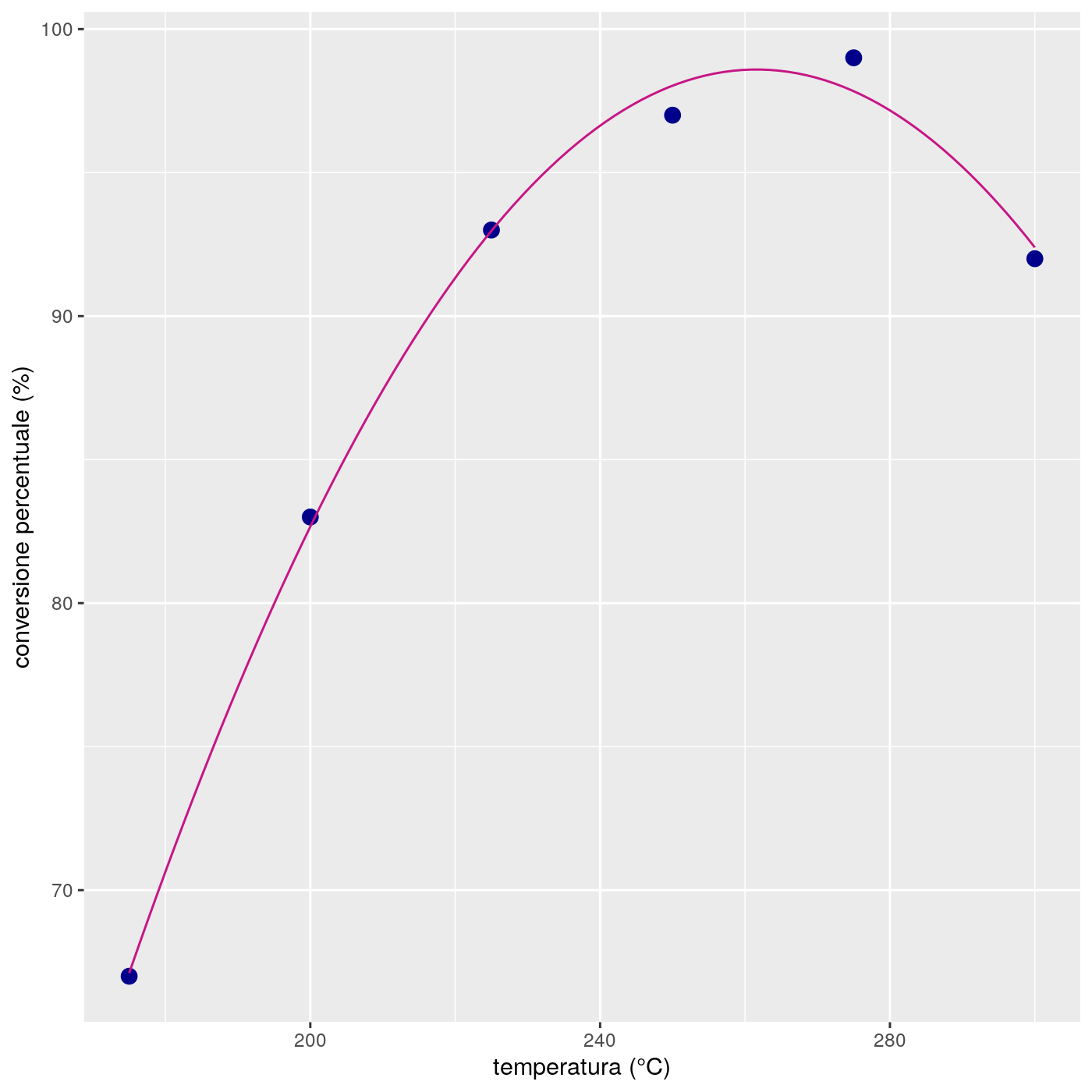

Figura 18.8: Gafico della previsione col modello quadratico