Capitolo 17 Reti Neurali (Neural Networks: NN)
17.1 Introduzione
La letteratura statistica sulle tecniche di previsione/modellazione sta crescendo in maniera molto rapida. Ogni giorno compaiono nuove tecniche applicare a progetti di data-mining a di business intelligence, e i nuovi sviluppi permettono al ricercatore di ottenere previsioni sempre più precise.
In questo capitolo vorremo introdurre molto brevemente le basi dell’analisi delle reti neurali per problemi di classificazione.
17.2 Esempio: Dati del Titanic
Qusto esempio usa i veri dati sulla sopravvivenza dei passeggeri del Titanic al suo affondamento.
L’obiettivo dello studio è trovare un modello predittivo per stabilire la probabilità di decesso per ciascun passeggero sulla base della sua età (Age), del suo sesso (Gender), e della classe (Class) di viaggio.
Vediamo prima alcuni riepiloghi del dataset:
## Class Gender Age Status
## 1 Coach Female 20 Survived
## 2 Coach Female 21 Survived
## 3 Coach Female 26 Survived
## 4 Coach Female 26 Died
## 5 Coach Female 36 Survived
## 6 Coach Female 41 Survived## Class Gender Age Status
## Coach:1876 Female: 470 Min. : 1.00 Died :1490
## First: 325 Male :1731 1st Qu.:31.00 Survived: 711
## Median :48.00
## Mean :47.12
## 3rd Qu.:64.00
## Max. :80.00E quindi caricahiamo il package usato per le analisi
Possiamo poi costruire alcune tabelle per aiutare a descrivere la relazione tra la probabilità di decesso e le variabili esplicative
##
## Coach First
## Died 1368 122
## Survived 508 203##
## Coach First
## Died 72.92 37.54
## Survived 27.08 62.46##
## Female Male
## Died 126 1364
## Survived 344 367##
## Female Male
## Died 26.81 78.80
## Survived 73.19 21.20## , , = Female
##
##
## Coach First
## Died 122 4
## Survived 203 141
##
## , , = Male
##
##
## Coach First
## Died 1246 118
## Survived 305 62## , , = Female
##
##
## Coach First
## Died 37.54 2.76
## Survived 62.46 97.24
##
## , , = Male
##
##
## Coach First
## Died 80.34 65.56
## Survived 19.66 34.44Le tabelle qui sopra mostrano i conteggi e le percentuali dei passeggeri deceduti e sopravvissuti per ciascuna combinazione dei fattori Sex e Class. Appaiono in maniera evidente alcune relazioni, ma la loro interpretazione generale non è sempre molto semplice. Potremmo quindi pensare che la relazione tra le variabili indipendenti e la variabile dipendente sia complessa e, forse, anche non lineare.
Il grafico che segue mostra se esistono relazioni tra Status e Age:
library(ggplot2)
ggp <- ggplot(data=titanic, mapping = aes(y=Age, x=Status)) +
geom_boxplot() +
ggtitle("Boxplot di Age Vs. Status")
print(ggp)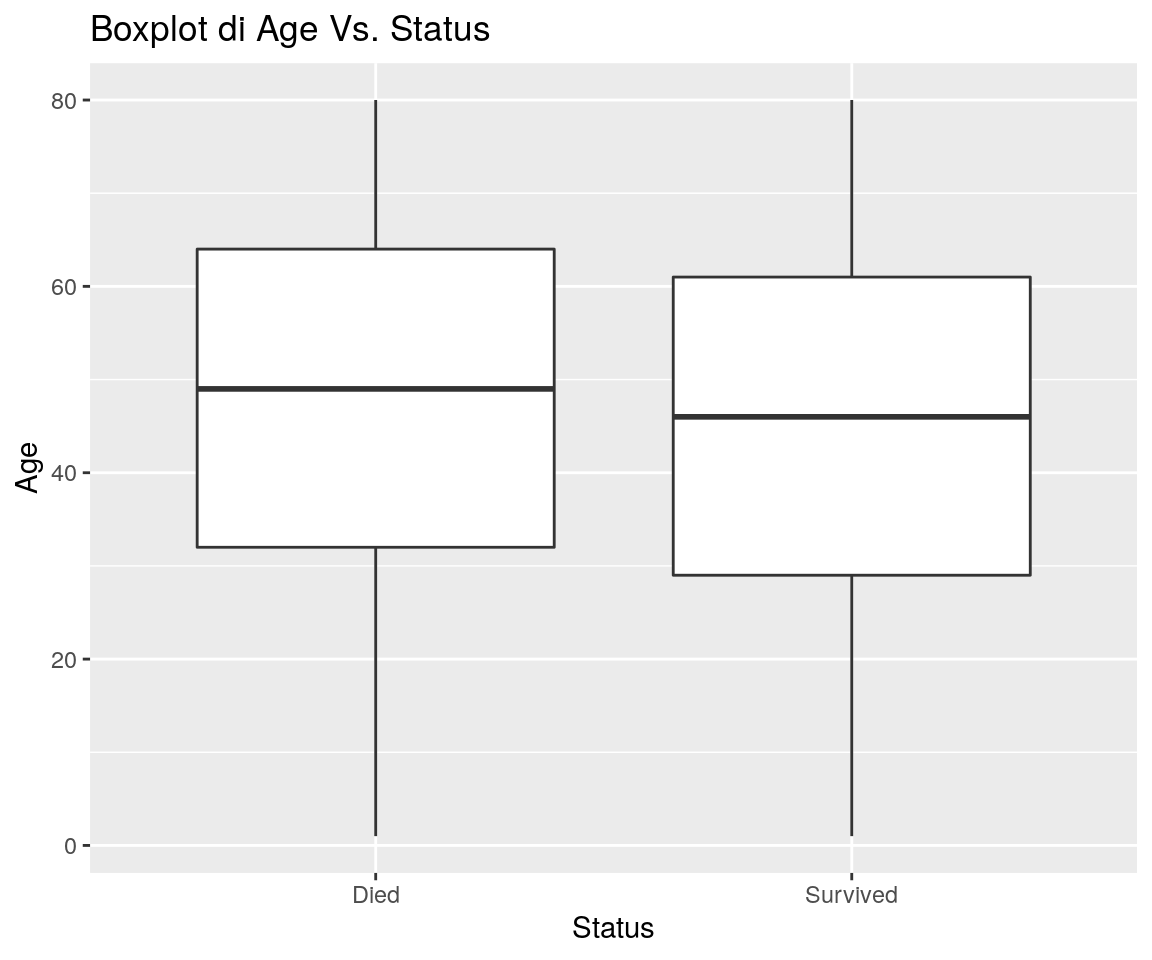
Figura 17.1: Box-plot of Age within levels of Status
Sembra che i passaggeri sopravvissuti abbiamo un’età leggermente inferiore.
Ora possiamo provare un modello per prevedere la probabilità di morte Vs. le variabili indipendenti.
Il package R nnet fornisce una funzione nnet() per adattare ai dati una rete neurale a singolo strato nascosto (single-hidden-layer). nnet() produce in output un oggetto di classe nnet.formula e nnet.
La instassi usata per costruire un oggetto nnet è molto simile a quella usata per i modelli lineari (generalized):
## # weights: 16
## initial value 1500.344084
## iter 10 value 1371.984175
## iter 20 value 1203.212858
## iter 30 value 1146.752674
## iter 40 value 1118.436406
## final value 1117.513762
## convergedIl parametro size della chiamata nnet() qui sopra specifica il numero di unità (neuroni) nello strato nascosto.
La tabella che segue mostra la matrice di confusione per il modello adattatto
titanic$pred <- as.vector(predict(nn0, type="raw"))
titanic$pred_class <- factor(ifelse(titanic$pred < 0.5, "Died", "Survived"))
library(caret)## Loading required package: lattice## Confusion Matrix and Statistics
##
## Reference
## Prediction Died Survived
## Died 1364 367
## Survived 126 344
##
## Accuracy : 0.776
## 95% CI : (0.758, 0.7933)
## No Information Rate : 0.677
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.4381
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Sensitivity : 0.9154
## Specificity : 0.4838
## Pos Pred Value : 0.7880
## Neg Pred Value : 0.7319
## Prevalence : 0.6770
## Detection Rate : 0.6197
## Detection Prevalence : 0.7865
## Balanced Accuracy : 0.6996
##
## 'Positive' Class : Died
## Se vogliamo ottenere una previsione della probabilità di decesso per diversi livelli delle variabili indipendenti, possiamo calcolare una tabella dei valori delle variabili indipendenti e quindi prevedere le probabilità.
Nell’esempio che segue, sono prodotti i valori medi di probabilità per ogni combinazione dei livelli dei fattori Class e Gender, insieme all’età media:
##
## Attaching package: 'dplyr'## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, unionds_pred <- titanic %>%
group_by(Class, Gender) %>%
summarise(Age = mean(Age, na.rm=TRUE))
ds_pred$prob <- predict(nn0, newdata = ds_pred, type="raw")
ds_pred## # A tibble: 4 x 4
## # Groups: Class [2]
## Class Gender Age prob[,1]
## <fct> <fct> <dbl> <dbl>
## 1 Coach Female 43.8 0.626
## 2 Coach Male 47.5 0.196
## 3 First Female 50.2 0.976
## 4 First Male 47.7 0.34317.3 Esempio: dati MNIST (deep learning)
In questo esempio vediamo una applicazione di rete neurale profonda usando il package Keras.
Si vuole trovare un modo per “riconoscere” il carattere scritto a mano da personw.
I dati sono raccolte di immagini in scala di grigio di dimensioni 28x28, contenenti “foto” di
cifre numeriche scritte a mano.
Queste foto sono in sostanza array numerici con valori di gradazioni di grigio (valori compresi tra 0 e 255) per
ciascun pixel.
# da https://tensorflow.rstudio.com/tensorflow/articles/tutorial_mnist_beginners.html
knitr::include_graphics("images/MNIST-Matrix.png")
Cominciamo caricando i dati da internet, separati in dati di training e dati di test:
library(keras)
mnist <- dataset_mnist()
x_train <- mnist$train$x
y_train <- mnist$train$y
x_test <- mnist$test$x
y_test_input <- mnist$test$yOra prepariamo i dati per la rete. In questo caso “stendiamo” i valori dei
pixel su un vettore unico con 784 elementi per ciascuna immagine e convertiamo i valori originali in
frazioni comprese tra 0 e 1.
I valori delle variabili dipendenti sono convertiti in categoriali, poiché indicano il carattere tra “0” e “9”.
# reshape
x_train <- array_reshape(x_train, c(nrow(x_train), 784))
x_test <- array_reshape(x_test, c(nrow(x_test), 784))
# rescale
x_train <- x_train / 255
x_test <- x_test / 255
y_train <- to_categorical(y_train, 10)
y_test <- to_categorical(y_test_input, 10)Per questo esempio usiamo una rete neurale relativamente semplice, fatta di 1 strato di input,
uno strato di 256 neuroni, uno strato (layer_dropout(rate = 0.4)) che “stabilizza”
la struttura dei parametri, uno strato con 128 neuroni, un’ulteriore strato che stabilizza la
rete, ed uno strato di output con 10 neuroni che possono assumere valori compresi tra 0 e 1 (“softmax”).
Questi 10 valori possono essere visti come “probabilità stimate” che la singola immagine rappresenti
ciascuna delle 10 cifre. Ovviamente la cifra “scelta” dalla rete sarà quella con la probabilità più alta.
Vediamo quindi il riepilogo del modello della rete con il conteggio dei parametri: un totale di 235146.
model <- keras_model_sequential()
model %>%
layer_dense(units = 256, activation = 'relu', input_shape = c(784)) %>%
layer_dropout(rate = 0.4) %>%
layer_dense(units = 128, activation = 'relu') %>%
layer_dropout(rate = 0.3) %>%
layer_dense(units = 10, activation = 'softmax')
summary(model)## Model: "sequential"
## __________________________________________________________________________________
## Layer (type) Output Shape Param #
## ==================================================================================
## dense (Dense) (None, 256) 200960
## __________________________________________________________________________________
## dropout (Dropout) (None, 256) 0
## __________________________________________________________________________________
## dense_1 (Dense) (None, 128) 32896
## __________________________________________________________________________________
## dropout_1 (Dropout) (None, 128) 0
## __________________________________________________________________________________
## dense_2 (Dense) (None, 10) 1290
## ==================================================================================
## Total params: 235,146
## Trainable params: 235,146
## Non-trainable params: 0
## __________________________________________________________________________________Le prossime istruzioni definiscono come la procedura dovrà determinare, attraverso
un processo di minimizzazione di una distanza tra le immagini osservate e quanto “interpretato”
dalla rete neurale (categorical_crossentropy), i valori dei parametri per permettere il riconoscimento
delle cifre scritte stesse.
Il grafico successivo (plot(history)) mostra il percorso fatto dal processo di ottimizzazione, in cui
si vede quanto la rete riconosce “bene” le cifre, in termini di funzione di perdita
(loss) e di percentuale di cifre correttamente riconosciute (accuracy), per le osservazioni di training e per
le osservazioni di “validazione” (“validation”: dati estratti dai dati di
training, in questo caso per una frazione di 0.2 del totale, per vedere come la rete riconosce bene le cifre durante il training).
Infine, vengono generate le previsioni per i dati di test e calcolata la matrice di confusione.
model %>% compile(
loss = 'categorical_crossentropy',
optimizer = optimizer_rmsprop(),
metrics = c('accuracy')
)
history <- model %>% fit(
x_train, y_train,
epochs = 30, batch_size = 128,
validation_split = 0.2
)
plot(history)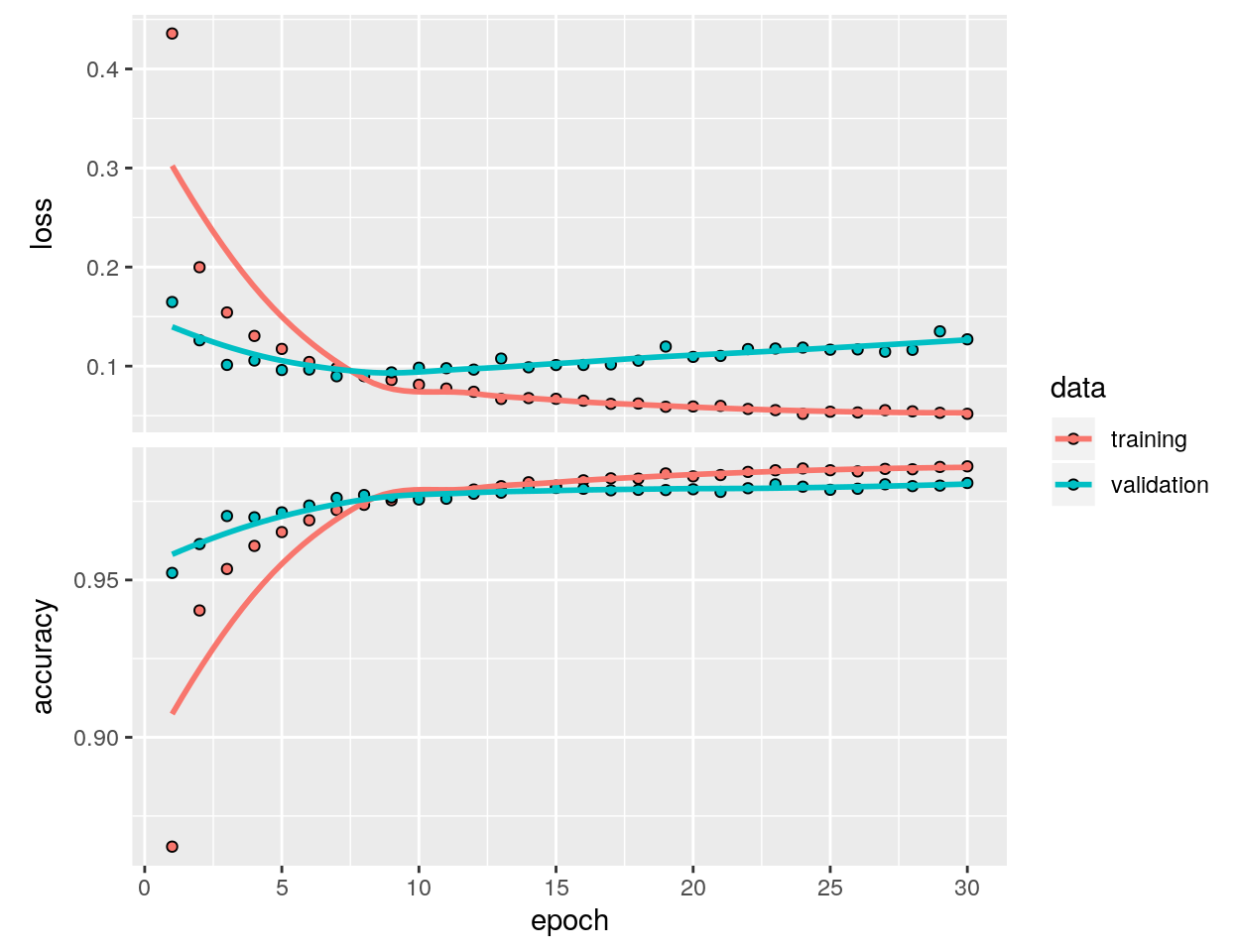
y_test_fit <- model %>% predict_classes(x_test)
confusionMatrix(factor(y_test_fit), reference = factor(y_test_input))## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1 2 3 4 5 6 7 8 9
## 0 971 0 3 0 2 3 3 1 3 4
## 1 1 1125 0 0 0 0 3 4 2 3
## 2 1 3 1016 2 3 0 0 11 3 0
## 3 1 0 2 996 0 11 1 1 3 3
## 4 0 0 1 0 961 1 3 0 2 6
## 5 1 2 0 3 0 866 3 0 6 4
## 6 3 2 1 0 4 7 942 0 3 0
## 7 1 1 6 6 3 1 0 1006 4 7
## 8 1 2 3 2 1 2 3 1 942 3
## 9 0 0 0 1 8 1 0 4 6 979
##
## Overall Statistics
##
## Accuracy : 0.9804
## 95% CI : (0.9775, 0.983)
## No Information Rate : 0.1135
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.9782
##
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: 0 Class: 1 Class: 2 Class: 3 Class: 4 Class: 5
## Sensitivity 0.9908 0.9912 0.9845 0.9861 0.9786 0.9709
## Specificity 0.9979 0.9985 0.9974 0.9976 0.9986 0.9979
## Pos Pred Value 0.9808 0.9886 0.9779 0.9784 0.9867 0.9785
## Neg Pred Value 0.9990 0.9989 0.9982 0.9984 0.9977 0.9971
## Prevalence 0.0980 0.1135 0.1032 0.1010 0.0982 0.0892
## Detection Rate 0.0971 0.1125 0.1016 0.0996 0.0961 0.0866
## Detection Prevalence 0.0990 0.1138 0.1039 0.1018 0.0974 0.0885
## Balanced Accuracy 0.9944 0.9949 0.9910 0.9918 0.9886 0.9844
## Class: 6 Class: 7 Class: 8 Class: 9
## Sensitivity 0.9833 0.9786 0.9671 0.9703
## Specificity 0.9978 0.9968 0.9980 0.9978
## Pos Pred Value 0.9792 0.9720 0.9813 0.9800
## Neg Pred Value 0.9982 0.9975 0.9965 0.9967
## Prevalence 0.0958 0.1028 0.0974 0.1009
## Detection Rate 0.0942 0.1006 0.0942 0.0979
## Detection Prevalence 0.0962 0.1035 0.0960 0.0999
## Balanced Accuracy 0.9905 0.9877 0.9826 0.9840Abbiamo un’accuratezza che si attesta intorno a 0.98. Un bel risultato direi!
Probabilmente, proseguendo oltre le 30 epoche (cicli) di ottimizzazione si potevano
migliorare ulteriormente le performance. Sono disponibili anche altre
per ottenere risultati probabilmente ancora migliori, ma avremmo bisogno di un sito
solo per questo.
17.4 Alcuni cenni di teoria sulle Reti Neurali
Le reti neurali possono essere considerate un tipo di regressione non linerare che prende un insieme di input (variabili esplicative), le trasforma e pesa con un insieme di unità nascoste e strati nascosti per produrre poi un insieme di output o previsioni (a loro volta trasformate).
La fgura che segue è un esempio di una rete neurale feed forward composta di quattro input, uno strato intermedio nascosto che contiene tre unità, e uno strato di output che contiene due output.

Gli output dei nodi in uno strato sono gli input dello strato successivo. Gli input di ciascun nodo sono combinati usando una combinazione lineare pesata. Il risultato è quindi usualmente modificata tramite una funnzione non lineare prima di essere passata in output. Per esempio, gli input nel neurone nascosto \(j\) nella figura precedente sono combinati per dare
\(z_j=b_j+\sum_{i=1}^4 w_{i,j} x_i\).
Nello strato nascosto, questo è quindi modificato usando una funzione non lineare quale la sigmoide,
\(\phi(z)=\dfrac{1}{1+e^{-z}}\),
per produrre l’input dello strato successivo. Questo permette alla formula di ridurre l’effetto dei valori di input estremi, e quindi rendere la rete più robusta alla presenza di outlier. Inoltre, le funzioni di attivazione aggiungono una componente non lineare alla rete, che altrimenti risulterebbe in una semplice funzione lineare, per quanto complicata.
I valori dei parametri \(b_1\),\(b_2\),\(b_3\) e \(w_{1,1}, \cdots ,w_{4,3}\) sono “appresi” a partire dai dati.
I pesi usualmente assumono inizialmente valori casuali, e sono quindi aggiornati usando i dati osservati. Di conseguenza, si ha un elemento di casualità nelle previsioni prodotte da una rete neurale; e pertanto la rete è usualmente addestrata diverse volte usando punti di partenza differenti, e producendo quindi una media dei diversi risultati.
Il numero di strati nascosti, nonché il numero di nodi in ogni strato nascosto, deve essere specificato prima dell’analisi.