Capitolo 3 Multidimensional Scaling (MDS)
3.1 Introduzione
Il Multidimensional Scaling (MDS) è un insieme di tecniche per proiettare i punti provenienti da uno spazio multidimensionale in uno spazio di dimensionalità inferiore, meglio se con 2 o 3 sole dimensioni. L’obiettivo è cercare di riprodurre quanto possibile le distanze tra i punti originari ma in uno spazio di dimensionalità ridotta. L’input per l’MDS sono “dati di prossimità”, cioè le similarità o dissimilarità osservate tra tutte le coppie di osservazioni. La matrice di prossimità è usualmente visualizzata come una matrice triangolare inferiore di valori non negativi, con l’idea implicita che i valori sulla diagonale siano tutti zero e che la parte triangolare superiore della matrice sia un’immagine speculare della parte triangolare inferiore (cioè, la matrice è simmetrica).
Il problema generale dell’MDS può essere specificato, nella sua essenza, come segue: data una matrice di prossimità tra oggetti (cioè, osservazioni o variabili), si vuole ricostruire la mappa originaria quanto più precisamente quanto possibile. Un altro aspetto nel problema è che non si conosce a priori il numero di dimensioni in cui le entità fornite dovranno essere proiettate. Di conseguenza, la determinazione del numero di dimensioni è un altro problema da risolvere.
Nella sua versione più elementare, MDS è principalmente usato per visualizzare e identificare “gruppi” di punti, ma sono state sviluppate molte varianti per affrontare obiettivi più specifici quali l’individuazone di dimensioni latenti.
3.2 MDS metrico
La funzione R che implementa il cosiddetto MDS classico (o metrico) cmdscale().
3.2.1 Esempio: mds su dati costruiti ad-hoc
Come primo esempio, considereremo il dataset mds composto di dati artificiali.
Possiamo vederne alcune caratteristiche tramite:
## V1 V2 V3 V4 V5
## 1 3 4 4 6 1
## 2 5 1 1 7 3
## 3 6 2 0 2 6
## 4 1 1 1 0 3
## 5 4 7 3 6 2
## 6 2 2 5 1 0
## 7 0 4 1 1 1
## 8 0 6 4 3 5
## 9 7 6 5 1 4
## 10 2 1 4 3 1
o anche:
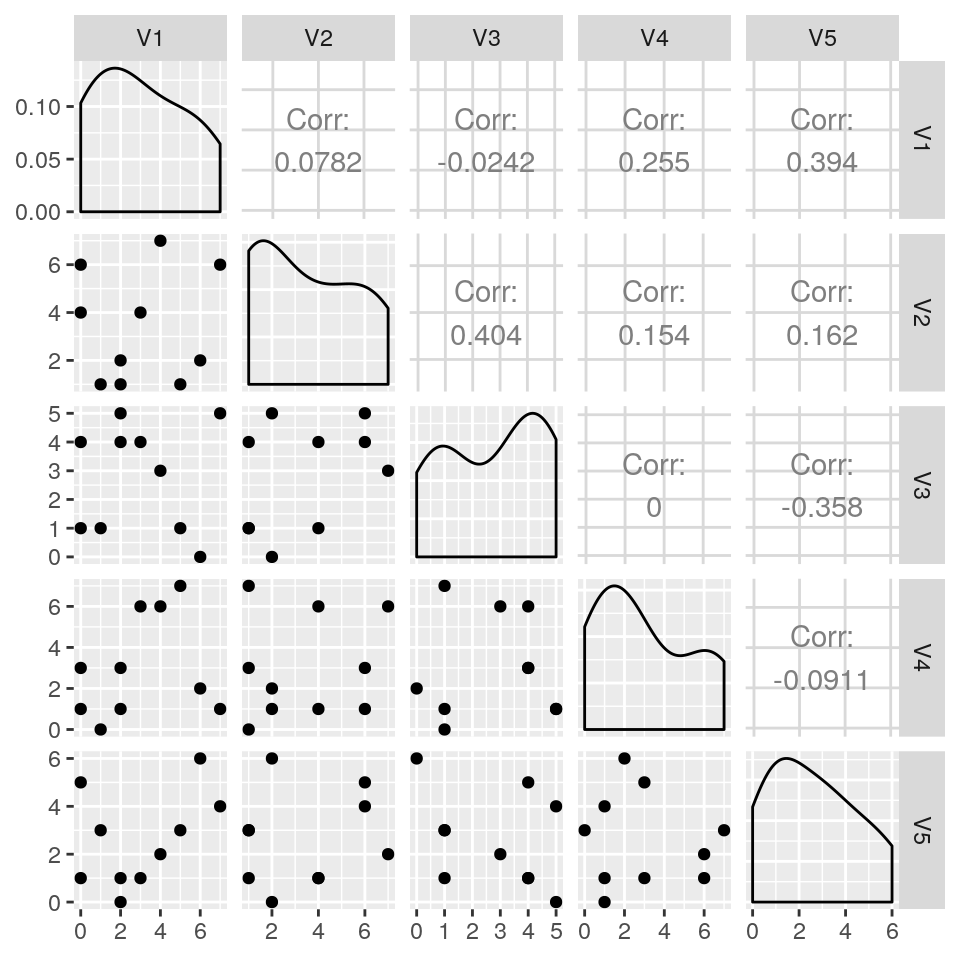
Come si vede, i valori delle singole entità (righe) del dataset hanno una distribuzione che risulta poco informativa anche per un osservatore attento. Obiettivo dell’MDS, è cercare di riprodurre le distanze relative tra gli oggetti su uno spazio di dimensioni ridotte. In tal modo si spera di riuscire ad ottenere una maggiore interpretabilità della configurazione o delle differenze nelle distanze.
Ora creiamo la matrice di prossimità calcolando le corrispondenti distanze Euclidee
tramite la funzione dist() (altre misure di distanza disponibili tramite l’argomento
method sono "maximum", "manhattan", "canberra", "binary" o
"minkowski"; si veda la pagina di help della funzione dist() per dettagli).
Applichiamo quindi lo scaling classico su questa matrice usando la funzione cmdscale(), usando
k=9 dimensioni e chiedendo anche che ne vengano salvati gli autovalori:
## Warning in cmdscale(D, k = 9, eig = TRUE): only 7 of the first 9 eigenvalues are >
## 0Alcune note:
- Quando le dissimilarità sono definite come distanze euclidee tra punti, questo tipo di MDS classico è equivalente alla PCA (si veda il capitolo su PCA e EFA), poiché le coordinate MDS sono identiche agli score (punteggi) delle corrispondenti componenti principali;
- Se alcuni autovalori risultano negativi, è possibile aggiungere una costante alle dissimilarità, oppure si suggerisce anche di ignorare gli autovalori negativi.
Un modo per determinare la dimensionalità della configrazione finale è tramite l’ooservazione degli autovalori.
La strategia usuale è quella di tracciare gli autovalori (asse delle y) Vs. il numero di dimensioni (asse delle x) e quindi identificare la dimensione
oltre la quale gli autovalori diventano “stabili” (cioè, non cambiano in maniera evidente). A quella dimensione
si potrà osservare un “gomito” che mostra dove si presenta la stabilità. La speranza è che la dimensione cui si raggiunge la stabilità sia
piccola, usualmente dell’ordine di 2 o 3, così da rendere più semplice la lettura dei valori nello spazio ridotto.
Il grafico degli autovalori per il nostro esempio è ottenuto come:
eig <- X_mds$eig
dims <- 1:attr(D, "Size")
eig <- data.frame(Dimensioni = dims, Autovalore = eig)
ggp <- ggplot(eig, aes(x = Dimensioni, y = Autovalore)) +
geom_point() +
geom_line() +
scale_x_continuous("Dimensioni", breaks = dims) +
geom_hline(yintercept = 0, linetype = "dashed")
print(ggp)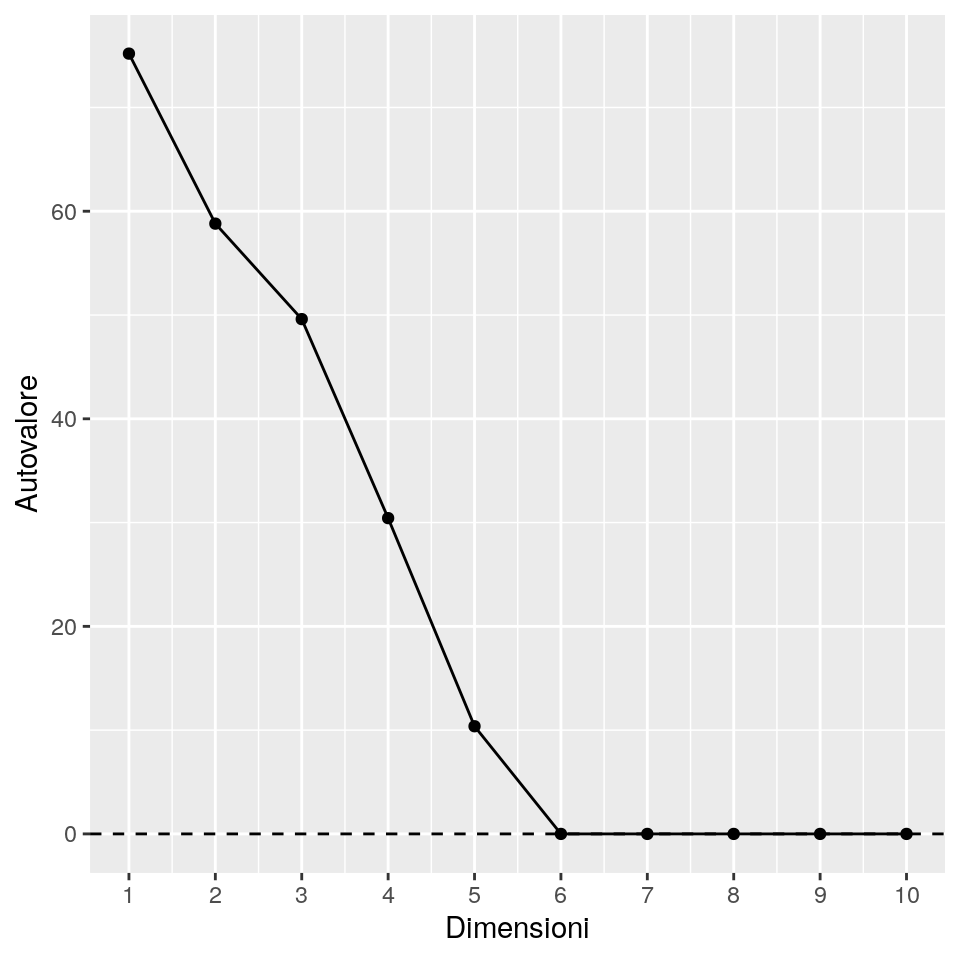
Si noti come nel dataset originario vi siano 5 variabili, e (in maniera non sorprendente) gli autovalori oltre al quinto siano essenzialmente nulli e quindi solo le prime cinque colonne di punti riprodotti rappresentino le distanze euclidee. Inoltre, la soluzione con 5 dimensioni ottiene la riproduzione completa delle distanze osservate. Si può verificare questo risultato confrontando le distanze originali con quelle calcolate con le cooordinate della soluzione di scaling a cinque dimensioni, usando il seguente codice:
ggp <- ggplot(data = data.frame(x = as.numeric(D),
y = as.numeric(dist(cmdscale(D, k = 5)))),
mapping = aes(x = x, y = y)) +
geom_point() +
geom_abline(intercept = 0, slope = 1) +
xlab("Distanze originarie") +
ylab("Distanze fitted (riprodotte)")
print(ggp)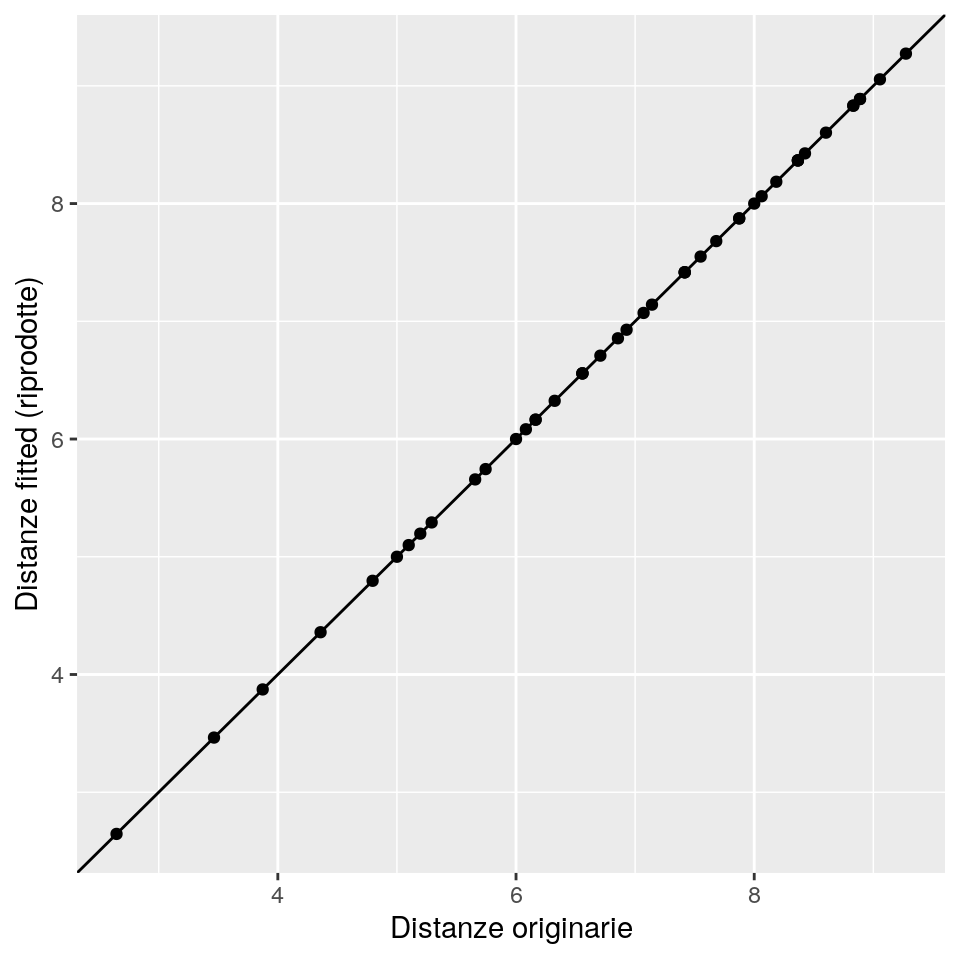
# Distanza massima tra distanze originarie e riprodotte
max(abs(dist(mds) - dist(cmdscale(D, k = 5))))## [1] 1.065814e-14Si possono anche calcolare alcuni criteri per la valutazione del’adattamento. I più popolari sono quelli introdotti da Mardia:
X_eig <- X_mds$eig
P1 <- cumsum(abs(X_eig))/sum(abs(X_eig))
P2 <- cumsum(X_eig^2)/sum(X_eig^2)
mardia <- data.frame(Dimensioni = rep(dims,2), P = c(P1, P2),
Criterio = rep(c("P1", "P2"),each=attr(D, "Size")))
ggp <- ggplot(data = mardia, aes(x = Dimensioni, y = P, colour=Criterio)) +
geom_point() +
geom_line() +
scale_x_continuous("Dimensioni", breaks = dims) +
scale_y_continuous("Valore", breaks = seq(0, 1, by = .1)) +
geom_hline(yintercept = .8, linetype = "dashed", color = "darkgray")
print(ggp)
I valori/criterio calcolati sono le somme percentuali cumulate degli autovalori (P1) e
le somme percentuali cumulate degli autovalori al quadrato (P2), al crescere del numero
di dimensioni selezionate. Valori superiori a 0.8 dovrebbero essere indicazione di una buona
riproduzione delle distanze. In questo esempio, entrambi i criteri suggeriscono che
una soluzione con 3 dimensioni sia una buona scelta. Questo sembra confermarsi
usando il grafico seguente, che confronta le distanze osservate con quelle ritornate
dalla soluzione con 3 dimensioni:
X_final <- X_mds$points[, 1:3]
D_hat <- dist(X_final, method = "euclidean")
D_all <- data.frame(Osservata = as.numeric(D), Riprodotta = as.numeric(D_hat))
ggplot(data = D_all, mapping = aes(x = Osservata, y = Riprodotta)) +
geom_point() +
scale_y_continuous(limits = c(0, 10)) +
scale_x_continuous(limits = c(0, 10)) +
geom_abline(linetype = "dashed", color = "gray")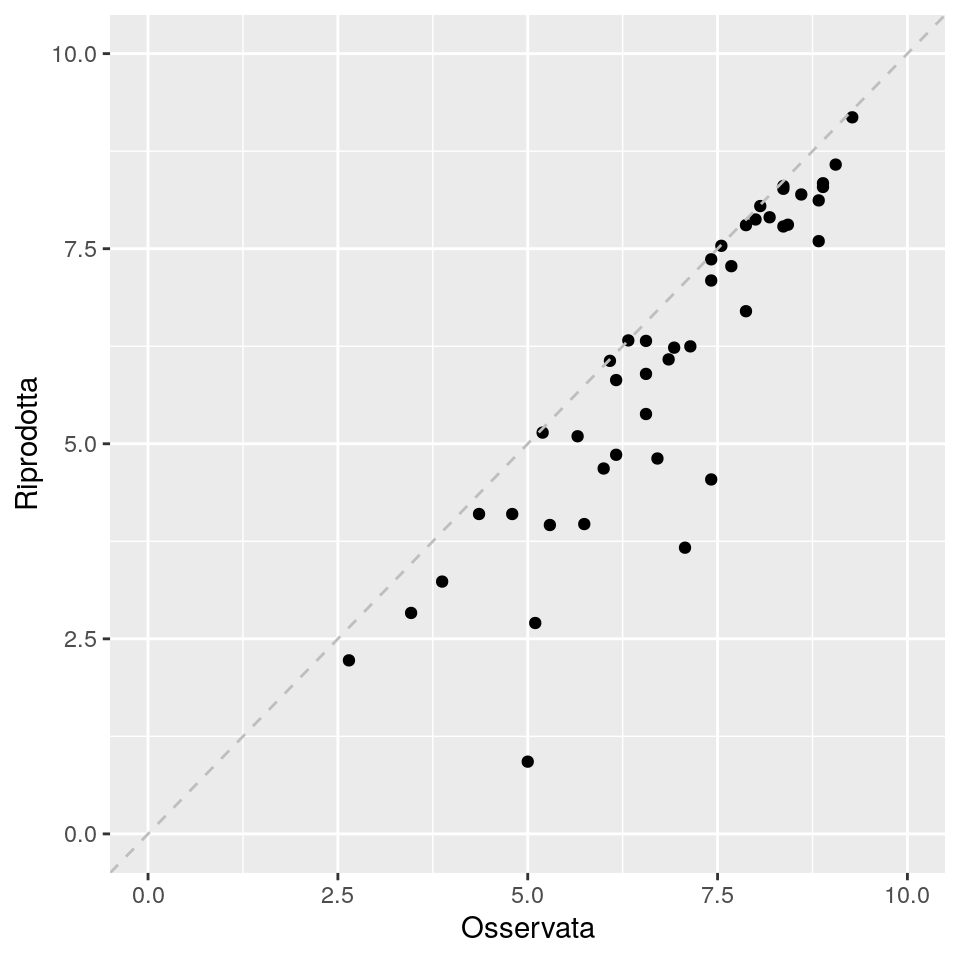
Infine, possiamo provare a tracciare le coordinate MDS per la soluzione tridimensionale:
o, alternativamente: (questo è un grafico 3D: provatelo nel “vostro” R)
library(rgl)
open3d()
with(data.frame(X_final),
plot3d(x = X1, y = X2, z = X3,
xlab = "X1", ylab = "X2", zlab = "X3", type = "p")
)Notate che MDS è finalizzato a preservare solo le distanze; di conseguenza le coordinate “fitted” (riprodotte) assolute possono risultare molto diverse dalle originali. In particolare, la distanza euclidea è invariante a trasformazini rigide (translazioni, rotazioni e riflessioni); pertanto, per interpretare in pratica le coordinate è anche meglio (usualmente) post-elaborare la soluzione applicando alcune trasformazioni.
3.2.2 Esempio: Illustrazione grafica su dati artificiali
Per illustrare meglio il comportamento dell’MDS metrico, produrremo un insieme di dati simulati:
x <- 1:10
y <- 1:10
comb <- expand.grid(x,y)
names(comb) <-c("x","y")
comb$z= 2 + 3 * comb$x - 2 * comb$y + runif(n = 100,min = -2, max = 2)Se provate a usare il codice che segue per rappresentare i dati su uno spazio tridimensionale, vedrete che i punti delle 3 variabili risultano quasi linearmente dipendenti, perché giacciono posizioni estremamente prossime ad un piano:
Questo farebbe pensare che gran parte della variabilità presente nelle distanze tra punti possa essere riprodotta con 2 sole dimensioni, invece delle 3 originarie.
Possiamo quindi produrre l’analisi MDS, chiedendo di “tenere” solo k = 3 dimensioni:
## $points
## [,1] [,2] [,3]
## [1,] -5.2419912 -6.2301983 -0.07849735
## [2,] -0.5990780 -5.6821688 0.31550855
## [3,] 0.5818861 -5.1341393 -0.23055695
## [4,] 3.7320532 -4.5861097 -0.24189723
## [5,] 8.2444479 -4.0380802 0.11666715
## [6,] 12.7025610 -3.4900506 0.46049171
## [7,] 12.9864084 -2.9420211 -0.32918042
## [8,] 18.5159706 -2.3939916 0.30558967
## [9,] 21.3814863 -1.8459620 0.21695402
## [10,] 23.0790139 -1.2979325 -0.18884177
## [11,] -7.6881818 -5.3937394 -0.17487066
## [12,] -4.1905904 -4.8457098 -0.09186997
## [13,] -0.1517441 -4.2976803 0.13810520
## [14,] 0.8590726 -3.7496507 -0.45416279
## [15,] 4.8557258 -3.2016212 -0.23564488
## [16,] 10.2440590 -2.6535917 0.36077532
## [17,] 13.3765686 -2.1055621 0.34464025
## [18,] 15.5779749 -1.5575326 0.07566967
## [19,] 18.3572074 -1.0095030 -0.03639569
## [20,] 19.4040895 -0.4614735 -0.61887032
## [21,] -7.1367315 -4.5572804 0.54274736
## [22,] -5.6535710 -4.0092508 0.07874147
## [23,] -3.0948894 -3.4612213 -0.09321313
## [24,] -0.4513594 -2.9131918 -0.24212767
## [25,] 2.3468012 -2.3651622 -0.34905322
## [26,] 7.5257232 -1.8171327 0.19050265
## [27,] 11.4278329 -1.2691031 0.38334782
## [28,] 13.6771177 -0.7210736 0.12737838
## [29,] 15.8170011 -0.1730441 -0.15829836
## [30,] 19.3800270 0.3749855 -0.05752936
## [31,] -10.7473020 -3.7208214 0.13019373
## [32,] -7.4883195 -3.1727919 0.14840161
## [33,] -5.8035199 -2.6247623 -0.26085042
## [34,] -1.9971330 -2.0767328 -0.09399817
## [35,] 1.2650258 -1.5287032 -0.07492781
## [36,] 6.1482294 -0.9806737 0.38432751
## [37,] 8.3081828 -0.4326442 0.10410067
## [38,] 12.4741717 0.1153854 0.36860065
## [39,] 14.6498480 0.6634149 0.09264325
## [40,] 15.1194929 1.2114445 -0.64657668
## [41,] -14.7473531 -2.8843624 -0.38812102
## [42,] -8.6586991 -2.3363329 0.39846709
## [43,] -8.0471397 -1.7883033 -0.30221681
## [44,] -4.6404801 -1.2402738 -0.24390813
## [45,] 0.4834860 -0.6922443 0.28072478
## [46,] 1.3430557 -0.1442147 -0.35261342
## [47,] 7.2753375 0.4038148 0.39151274
## [48,] 8.1033979 0.9518444 -0.25038159
## [49,] 11.8141106 1.4998739 -0.10950914
## [50,] 16.1395044 2.0479034 0.19827629
## [51,] -16.7992063 -2.0479034 -0.37741435
## [52,] -11.0893075 -1.4998739 0.30632503
## [53,] -9.1636814 -0.9518444 -0.03753198
## [54,] -5.6395629 -0.4038148 0.05267197
## [55,] -3.1969976 0.1442147 -0.15081333
## [56,] -0.9371294 0.6922443 -0.40390891
## [57,] 1.9660700 1.2402738 -0.48231179
## [58,] 6.5861643 1.7883033 -0.09450223
## [59,] 11.3783810 2.3363329 0.34004613
## [60,] 14.4098256 2.8843624 0.29646746
## [61,] -16.9887537 -1.2114445 0.13899018
## [62,] -14.4433659 -0.6634149 -0.03657428
## [63,] -11.4461332 -0.1153854 -0.08944300
## [64,] -9.0855741 0.4326442 -0.31519657
## [65,] -5.4409591 0.9806737 -0.19227252
## [66,] -3.4196939 1.5287032 -0.51015933
## [67,] 2.2088256 2.0767328 0.15148202
## [68,] 4.1503678 2.6247623 -0.18805308
## [69,] 9.1601090 3.1727919 0.30556275
## [70,] 8.9466054 3.7208214 -0.61916203
## [71,] -21.1050439 -0.3749855 -0.41088857
## [72,] -15.9636282 0.1730441 0.11848265
## [73,] -11.9706126 0.7210736 0.33601280
## [74,] -8.8474336 1.2691031 0.31734403
## [75,] -5.3107141 1.8171327 0.41096971
## [76,] -3.5946187 2.3651622 0.01021590
## [77,] 0.1060455 2.9131918 0.14835978
## [78,] 1.0403294 3.4612213 -0.46469024
## [79,] 5.7184917 4.0092508 -0.06111267
## [80,] 9.6377571 4.5572804 0.13639105
## [81,] -19.6843819 0.4614735 0.54275860
## [82,] -18.7618884 1.0095030 -0.07349301
## [83,] -16.4735111 1.5575326 -0.31884711
## [84,] -13.2576114 2.1055621 -0.31233812
## [85,] -7.9097172 2.6535917 0.27310110
## [86,] -6.6415290 3.2016212 -0.24927920
## [87,] -0.8855126 3.7496507 0.44698316
## [88,] 1.2647463 4.2976803 0.16412382
## [89,] 5.3956273 4.8457098 0.41909047
## [90,] 6.8615883 5.3937394 -0.04958583
## [91,] -21.6781831 1.2979325 0.56922892
## [92,] -19.4221617 1.8459620 0.31508878
## [93,] -15.5408653 2.3939916 0.50228222
## [94,] -15.4384517 2.9420211 -0.33665716
## [95,] -11.9575758 3.4900506 -0.25819547
## [96,] -6.7960315 4.0380802 0.27664158
## [97,] -3.9980997 4.5861097 0.16965391
## [98,] -1.1667711 5.1341393 0.07173495
## [99,] 0.8322864 5.6821688 -0.25218221
## [100,] 3.5326993 6.2301983 -0.38565054
##
## $eig
## [1] 1.189076e+04 8.250000e+02 9.053939e+00 7.993961e-13 4.944858e-13
## [6] 4.942374e-13 3.995281e-13 2.799741e-13 2.687761e-13 1.828252e-13
## [11] 1.576329e-13 1.396306e-13 1.382952e-13 1.368571e-13 1.287744e-13
## [16] 1.229743e-13 1.174880e-13 8.794482e-14 8.665997e-14 6.907715e-14
## [21] 6.695500e-14 6.280735e-14 5.862005e-14 5.085285e-14 4.320436e-14
## [26] 3.886484e-14 3.847605e-14 3.544578e-14 3.535093e-14 3.261722e-14
## [31] 3.124494e-14 2.976257e-14 2.928980e-14 2.663070e-14 2.564074e-14
## [36] 2.229550e-14 2.185424e-14 1.984045e-14 1.889922e-14 1.716006e-14
## [41] 1.670791e-14 1.606275e-14 1.457197e-14 1.283396e-14 1.207531e-14
## [46] 1.037615e-14 9.708511e-15 9.418884e-15 7.696303e-15 2.747032e-15
## [51] -3.585061e-16 -4.784240e-16 -1.309556e-15 -3.427064e-15 -4.621032e-15
## [56] -4.760164e-15 -5.126723e-15 -7.374710e-15 -7.883486e-15 -7.926375e-15
## [61] -9.101947e-15 -9.255564e-15 -9.370807e-15 -9.637359e-15 -1.214696e-14
## [66] -1.288914e-14 -1.349569e-14 -1.575656e-14 -1.598363e-14 -2.082552e-14
## [71] -3.019552e-14 -3.582691e-14 -3.808436e-14 -3.847186e-14 -4.066344e-14
## [76] -4.683548e-14 -5.398514e-14 -5.622166e-14 -5.760095e-14 -5.937931e-14
## [81] -6.558168e-14 -7.041615e-14 -7.214025e-14 -7.460161e-14 -8.651525e-14
## [86] -9.213150e-14 -9.854006e-14 -1.108899e-13 -1.181369e-13 -1.289965e-13
## [91] -1.667020e-13 -1.806917e-13 -1.972153e-13 -3.156182e-13 -4.104236e-13
## [96] -5.528532e-13 -8.362698e-13 -1.063905e-12 -1.128478e-12 -4.850565e-12
##
## $x
## NULL
##
## $ac
## [1] 0
##
## $GOF
## [1] 1 1Qui di seguito il grafico dei primi 10 autovalori ed il grafico delle distanze riprodotte sulle prime 3 dimensioni:
eig <- mds_1$eig
dims <- 1:attr(D, "Size")
eig <- data.frame(Dimensioni = dims, Autovalore = eig)
ggp <- ggplot(eig[1:10,], aes(x = Dimensioni, y = Autovalore)) +
geom_point() +
geom_line() +
scale_x_continuous("Dimensioni", breaks = 1:attr(D, "Size")) +
geom_hline(yintercept = 0, linetype = "dashed")
print(ggp)
ggp <- ggplot(data = data.frame(x = as.numeric(D),
y = as.numeric(dist(cmdscale(D, k = 3)))),
mapping = aes(x = x, y = y)) +
geom_point() +
geom_abline(intercept = 0, slope = 1) +
xlab("Distanze osservate") +
ylab("Distanze riprodotte")
print(ggp)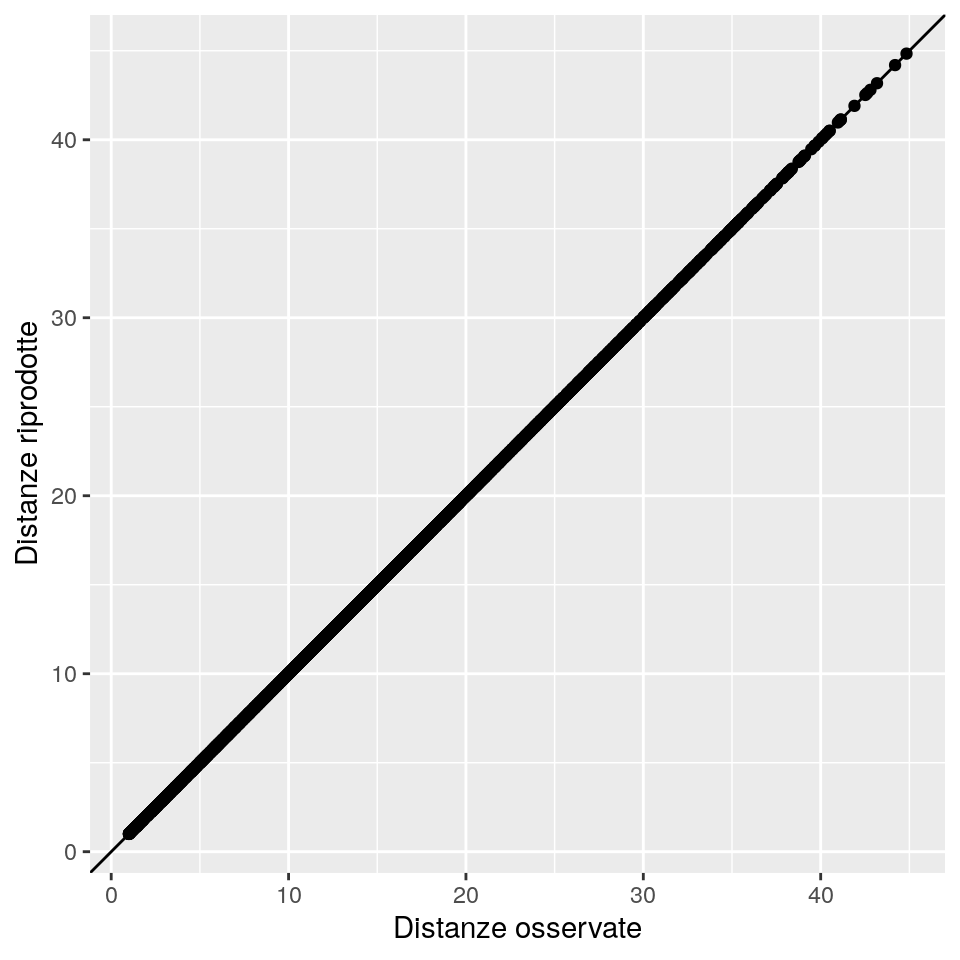
## [1] 2.267075e-13Come atteso, osservando il primo grafico si vede come le prime 3 componenti riproducano praticamente in maniera completa le distanze tra punti nel dataset.
L’ultimo valore numerico generato, invece, mostra il valore di differenza massima in valore assoluto tra le distanze osservate e quelle riprodotte.
Come si può vedere la differenza massima praticamente zero.
Il grafico che segue, invece, può essere solo manipolato usando la console R, e mostra i punti con la superficie che “ci passa attraverso”.
my_surface <- function(f, n=10, ...) {
ranges <- rgl:::.getRanges()
x <- seq(ranges$xlim[1], ranges$xlim[2], length=n)
y <- seq(ranges$ylim[1], ranges$ylim[2], length=n)
z <- outer(x,y,f)
surface3d(x, y, z, ...)
}
f <- function(x, y){
return(2 + 3 * x - 2*y)
}
open3d()
with(comb,
plot3d(x = x, y = y, z = z,
xlab = "x", ylab = "y", zlab = "z", type = "p", col="red")
)
my_surface(f, alpha=.7 )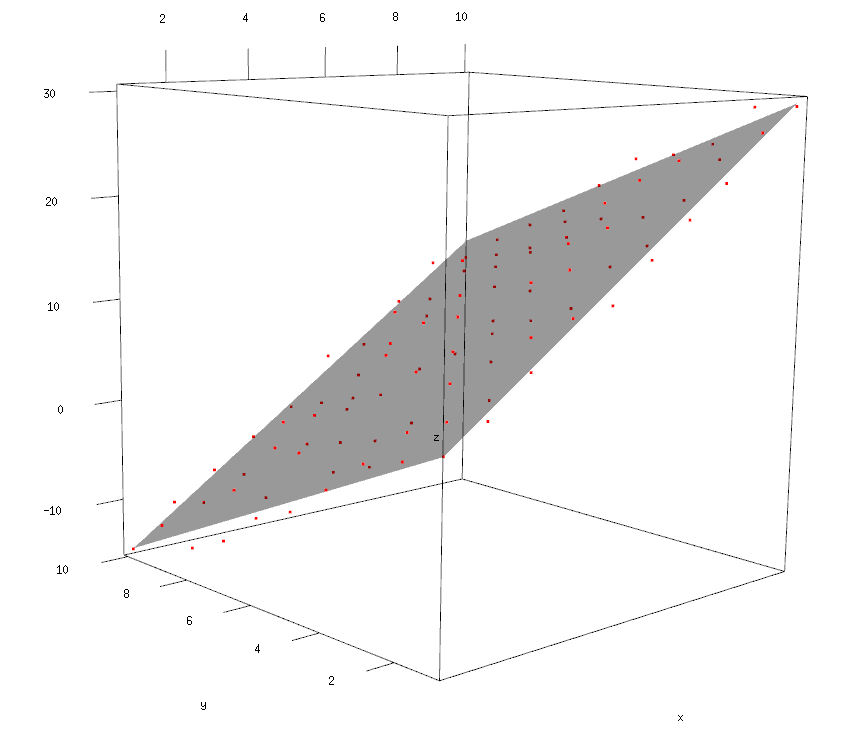
(Nota: il grafico ottenuto da voi può risultare leggermente diverso da quello rappresentato in questo testo, perché i punti sono stati generati con una componente di casualità.)
Il prossimo grafico, mostra i punti sul nuovo sistema di coordinate a 3 dimensioni generato dall’MDS:
open3d()
with(setNames(data.frame(mds_1$points), nm=c("x","y","z")),
plot3d(x = x, y = y, z = z,
xlab = "x", ylab = "y", zlab = "z", type = "p", col="red")
)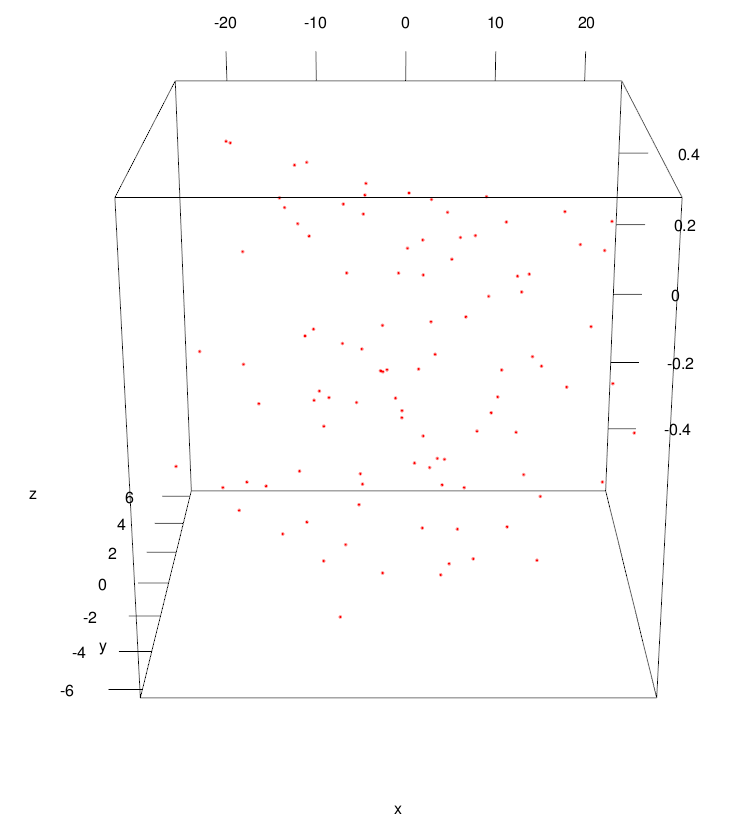
Come si vede, in questo caso le prime due dimensioni (x e y) hanno un range di variazione ampio, mentre la terza dimensione (z) che
“raccoglie” la quota di variabilità residua, ha un range di variabilità che è almeno di un ordine di grandezza inferiore
rispetto alle prime 2.
Se vogliamo analizzare la soluzione nelle prime 2 dimensioni, possiamo semplicamente impostare a 0 (o escludere) la terza componente nella soluzione MDS.
Questa è la proiezione dei punti 2D sulla superficie lineare:
# Soluzione riprodotta su 2 dimensioni
comb_3 <- setNames(data.frame(mds_1$points), c("x","y","z"))
comb_3$z <- 0open3d()
with(comb_3,
plot3d(x = x, y = y, z = z,
xlab = "x", ylab = "y", zlab = "z", type = "p", col="red")
)
(Nota: anche in questo caso il grafico ottenuto potrà variare per effetto della casualità.)
Come possiamo notare, i punti sono proiettati sulla superficie costruita a partire dalle prime due componenti. Qui sotto è mostrato il grafico che confronta le distanze osservate con quelle riprodotte:
ggp <- ggplot(data = data.frame(x = as.numeric(D),
y = as.numeric(dist(cmdscale(D, k = 2)))),
mapping = aes(x = x, y = y)) +
geom_point() +
geom_abline(intercept = 0, slope = 1) +
xlab("Distanze osservate") +
ylab("Distanze riprodotte")
print(ggp)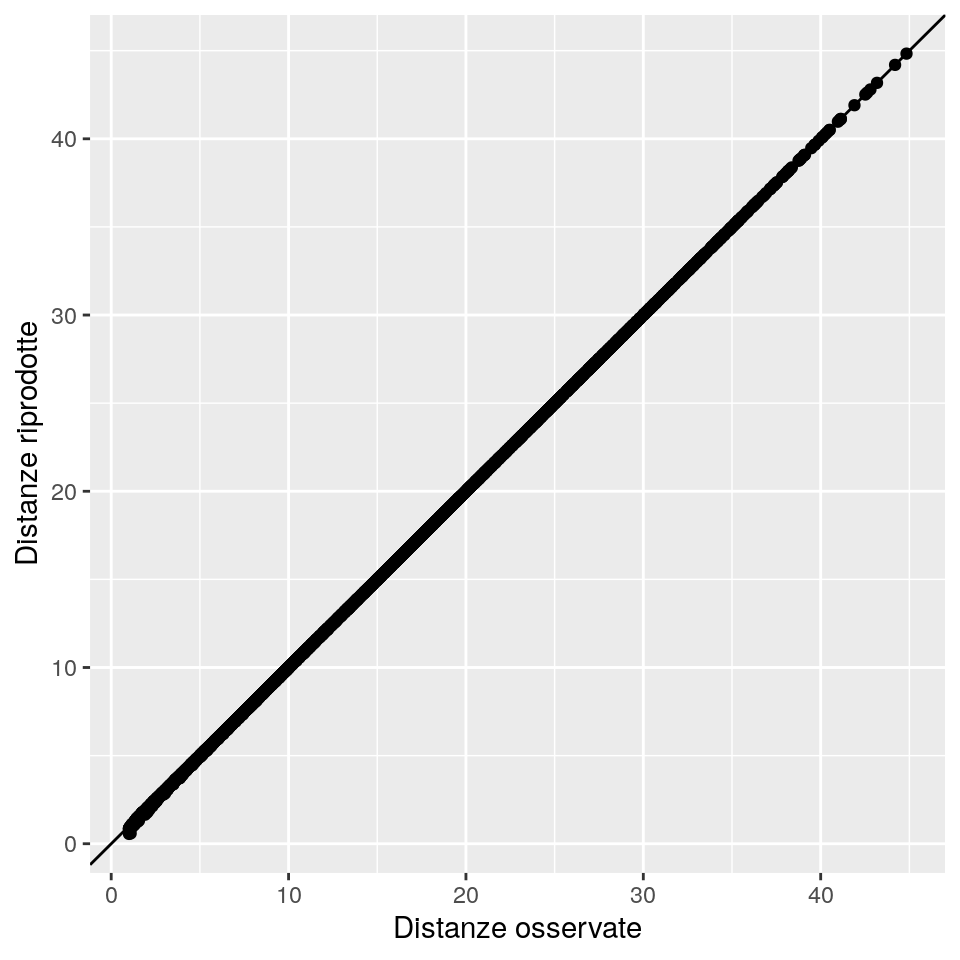
## [1] 0.5077681L’ultmo valore numerico riportato ci informa del fatto che la massima differenza tra le distanze osservate e quelle riprodotte tramite la soluzione MDS con 2 componenti è inferiore all’unità e (in questo caso lo sappiamo per costruzione) è dovuta interamente ad una componente casuale non “gestibile”.
3.2.3 Esempio: Teschi egizi
Come ulteriore esempio, un po’ più complesso, consideriamo i dati contenuti in skulls del package HSAUR2, che contengono le misurazioni su 30 teschi egizi provenienti da cinque epoche diverse (per un totale di 150 teschi). Le misure rilevate sono:
- mb –> ampiezza massima del teschio,
- bh –> altezza del teschio,
- bl –> lunghezza del teschio,
- nh –> altezza del naso del teschio.
La domanda cui si vuole rispondere è se queste misurazioni sono cambiate nel tempo. Valori non costanti delle misure dei teschi nel tempo possono essere indicazione di incroci con popolazioni migranti.
Cominciamo quindi col riassumere i dati, sia per via numerica che grafica:
## skulls$epoch: c4000BC
## mb bh bl nh
## Min. :119.0 Min. :121.0 Min. : 89.00 Min. :44.00
## 1st Qu.:128.0 1st Qu.:131.2 1st Qu.: 95.00 1st Qu.:49.00
## Median :131.0 Median :134.0 Median :100.00 Median :50.00
## Mean :131.4 Mean :133.6 Mean : 99.17 Mean :50.53
## 3rd Qu.:134.8 3rd Qu.:136.0 3rd Qu.:102.75 3rd Qu.:53.00
## Max. :141.0 Max. :143.0 Max. :114.00 Max. :56.00
## -------------------------------------------------------------
## skulls$epoch: c3300BC
## mb bh bl nh
## Min. :123.0 Min. :124.0 Min. : 90.00 Min. :45.00
## 1st Qu.:130.0 1st Qu.:129.2 1st Qu.: 97.00 1st Qu.:48.00
## Median :132.0 Median :133.0 Median : 98.50 Median :50.50
## Mean :132.4 Mean :132.7 Mean : 99.07 Mean :50.23
## 3rd Qu.:134.8 3rd Qu.:136.0 3rd Qu.:101.75 3rd Qu.:52.75
## Max. :148.0 Max. :145.0 Max. :107.00 Max. :56.00
## -------------------------------------------------------------
## skulls$epoch: c1850BC
## mb bh bl nh
## Min. :126.0 Min. :123.0 Min. : 87.00 Min. :45.00
## 1st Qu.:132.2 1st Qu.:131.0 1st Qu.: 92.25 1st Qu.:48.25
## Median :136.0 Median :133.5 Median : 96.00 Median :50.00
## Mean :134.5 Mean :133.8 Mean : 96.03 Mean :50.57
## 3rd Qu.:137.0 3rd Qu.:137.0 3rd Qu.: 99.75 3rd Qu.:52.75
## Max. :140.0 Max. :145.0 Max. :106.00 Max. :60.00
## -------------------------------------------------------------
## skulls$epoch: c200BC
## mb bh bl nh
## Min. :129.0 Min. :120.0 Min. : 86.00 Min. :46.00
## 1st Qu.:132.2 1st Qu.:130.0 1st Qu.: 91.25 1st Qu.:50.25
## Median :135.0 Median :132.0 Median : 94.50 Median :52.00
## Mean :135.5 Mean :132.3 Mean : 94.53 Mean :51.97
## 3rd Qu.:138.8 3rd Qu.:135.8 3rd Qu.: 97.75 3rd Qu.:53.75
## Max. :144.0 Max. :142.0 Max. :107.00 Max. :60.00
## -------------------------------------------------------------
## skulls$epoch: cAD150
## mb bh bl nh
## Min. :126.0 Min. :120.0 Min. : 81.0 Min. :44.00
## 1st Qu.:132.2 1st Qu.:126.0 1st Qu.: 91.0 1st Qu.:48.25
## Median :137.0 Median :130.0 Median : 94.0 Median :52.00
## Mean :136.2 Mean :130.3 Mean : 93.5 Mean :51.37
## 3rd Qu.:139.0 3rd Qu.:135.0 3rd Qu.: 97.0 3rd Qu.:54.00
## Max. :147.0 Max. :138.0 Max. :103.0 Max. :58.00
Per calcolare le distanze tra coppie di epoche useremo la distanza di Mahalanobis: una distanza
multivariata che tiene in considerazione anche le correlazioni esistenti tra le misure.
La funzione per il calcolo di questa distanza è mahalanobis(). Si applicherà quindi l’MDS classico
sulla matrice di distanze così calcolata.
# Calcola la matrice di varianza/covarianza tra le misure per ogni epoca
skulls_var <- tapply(X = 1:nrow(skulls), INDEX = skulls$epoch,
FUN = function(i) var(skulls[i, -1]))
# Calcola la matrice di varianza/covarianza entro-gruppi aggregata
S <- Reduce(`+`, skulls_var)*29/145
# Calcola le medie per ciascuna epoca per tutte le varibili misurate
# sfruttando il package dplyr
# Quindi converte il risultato in matrice
library(dplyr)
skulls_cen <- skulls %>%
group_by(epoch) %>%
summarise(mb = mean(mb), bh = mean(bh), bl = mean(bl), nh = mean(nh)) %>%
select(-epoch) %>%
as.matrix()
# Calcola le distanze di Mahalanobis delle misure medie tra tutte le coppie di epoche
skulls_mah <- as.dist(m = apply(X = skulls_cen, MARGIN = 1,
FUN = function(cen) mahalanobis(skulls_cen, cen, S)))
skulls_mah## 1 2 3 4
## 2 0.09103424
## 3 0.90307383 0.72893770
## 4 1.88112615 1.59401352 0.44311301
## 5 2.69681662 2.17568935 0.91087158 0.21928508La matrice mostrata qui sopra è la matrice delle distanze di Mahalanobis tra i valori medi delle misure delle
4 variabili calcolate nelle cinque epoche.
Ora provvediamo ad applicare il MDS metrico.
## Warning in cmdscale(skulls_mah, k = attr(skulls_mah, "Size") - 1, eig = TRUE):
## only 2 of the first 4 eigenvalues are > 0eig <- data.frame(Dimensioni = 1:attr(skulls_mah, "Size"), Autovalore = eig)
ggp <- ggplot(data = eig, mapping = aes(x = Dimensioni, y = Autovalore)) +
geom_point() +
geom_line() +
geom_hline(yintercept = 0, linetype = "dashed")
print(ggp)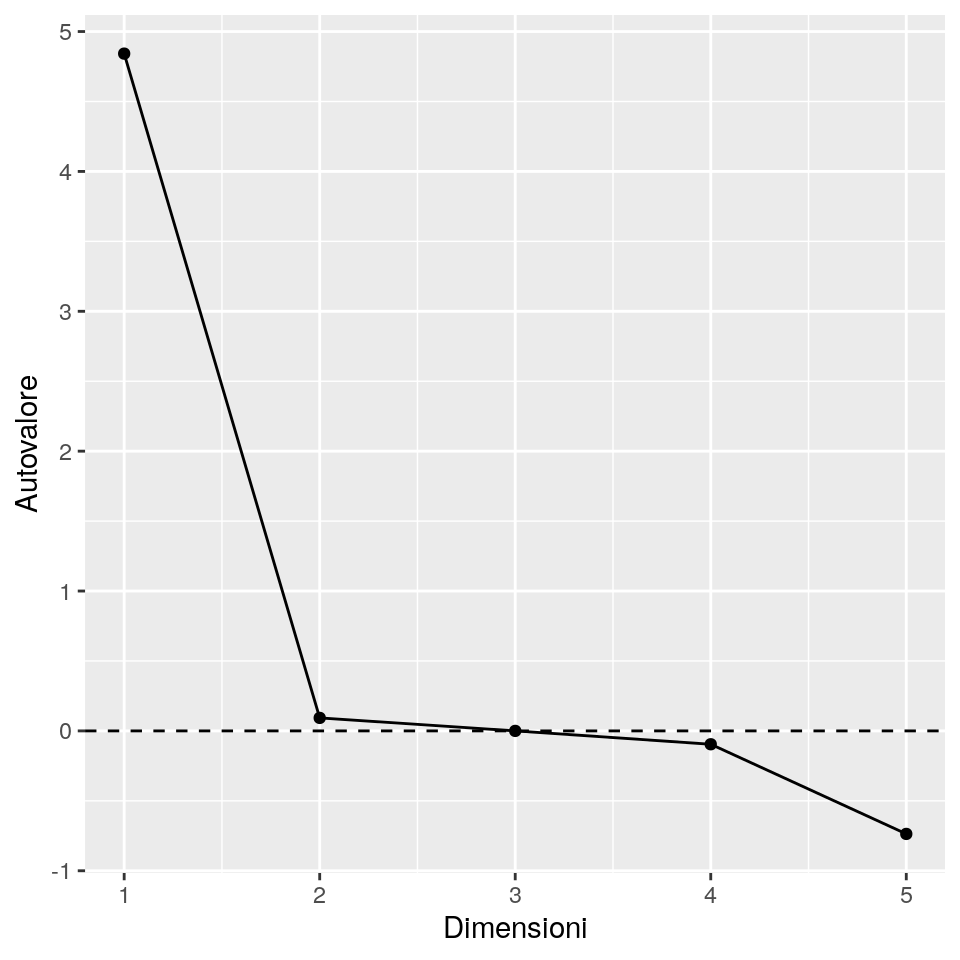
Il grafico degli autovalori MDS mostra che la soluzione ridotta è essenzialmente unidimensionale.
Useremo comunque i valori delle prime due cooordinate ottenute dall’MDS per fornire una mappa dei dati
che mostri se esiste una relazione tra le epoche.
ds <- data.frame(V1=skulls_mds[,1],V2= skulls_mds[,2], label = levels(skulls[, 1]))
ggp <- ggplot(data = ds, mapping = aes(x=V1, y = V2, label=label)) +
geom_point() +
geom_text(hjust = 0.5, vjust = -0.5) +
xlab("Prima dimensione") + ylab("Seconda dimensione") +
coord_fixed(ratio = 1, xlim = c(-2, 2), ylim = c(-2, 2))
print(ggp)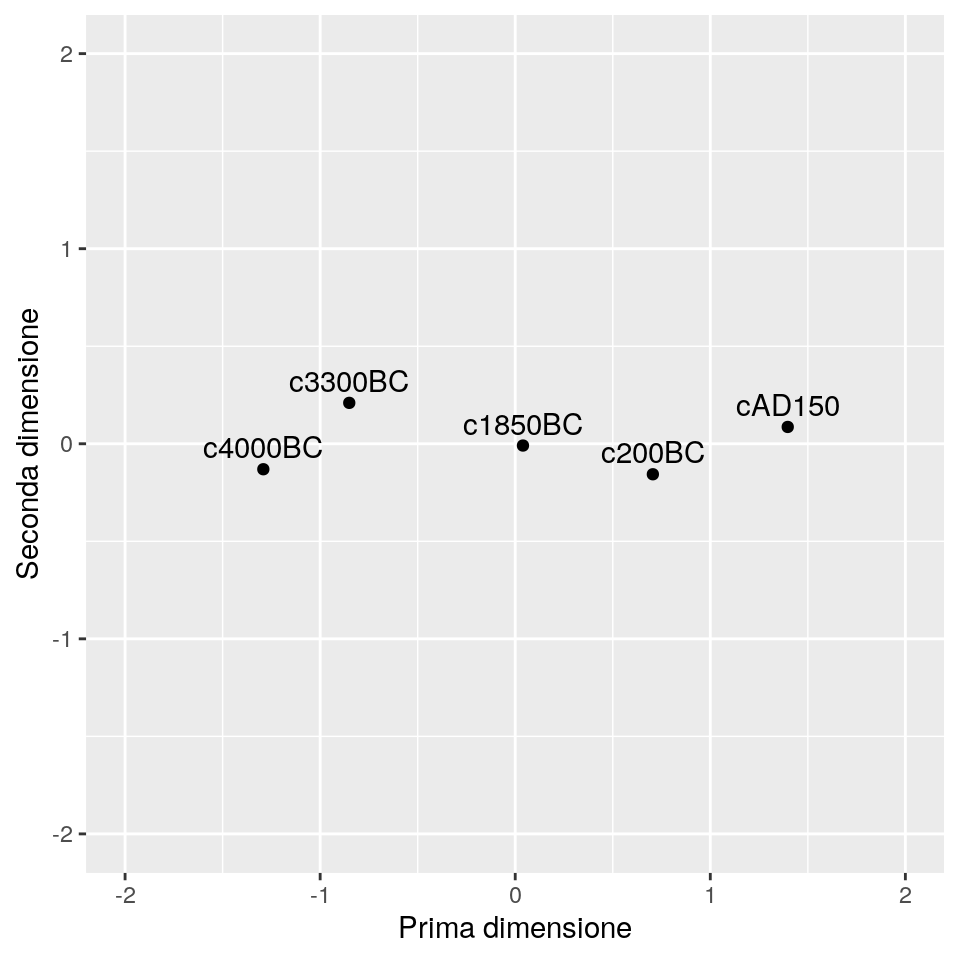
Si vede come la prima dimensione, quella con maggiore variabiità, è legata con l’ordinamento temporale delle cinque eopche analizzate, mostrando come i cambiamenti medi registrati nei tratti somatici delle popolazioni egizie possano essere dovuti alle interazioni avute nel tempo con le altre popolazioni.
3.3 MDS non metrico
In alcuni casi, quali in studi psicologici o nelle ricerche di mercato, le matrici di prossimità sono calcolate a partire da domande poste a soggetti che devono esporre le loro opinioni sulla somiglianza o dissomiglianza di oggetti. Per loro caratteristica, questi giudizi soggettivi ritornano solo un valore di ordinamento tra oggetti. Questi tipi di dato hanno portato allo sviluppo di metodi di MDS che utilizzano solo i valori di rango d’ordine delle prossimità per produrre una loro rappresentazione spaziale. Uno di questi metodi, chiamato MDS non metrico, usa la regressione monotòna per cercare quantità note come “disparità”, e quindi ricerca le coordinate richieste nella rappresentazione spaziale delle dissimilarità osservate che minimizza un valore-criterio introdotto da Kruskal, chiamato Stress. In parole povere, lo Stress rappresenta il grado di discordanza tra l’ordinamento in ranghi delle distanze adattate e l’ordinamento in ranghi delle dissimilarità osservate.
Per ogni valore del numero di dimensioni (\(m\)) di configurazione dello spazio, si cerca la configurazione con lo Stress più basso, \(S_m\); questa è chiamata la configurazione con miglior adattamento (best-fitting) in \(m\) dimensioni. Ovviamente al crescere di \(m\), \(S_m\) tenderà a decrescere. Una regola di massima per giudicare l’adattamento di un modello di MDS non metrico quindi è:
- \(S_m \ge 20\%\) ==> scarso,
- \(S_m = 10\%\) ==> discreto,
- \(S_m \le 5\%\) ==> buono.
3.3.1 Esempio: Ideologia politica
Prendiamo come esempio di applicazione di MDS non metrico il dataset wwiileaders. Abbiamo una rappresentazione spaziale dei giudizi di dissimilarità ideologica di alcuni leader e politici mondiali rilevanti all’epoca della seconda guerra mondiale. I soggetti intervistati hanno fornito dei giudizi su una scala a nove punti, con i punti estremi della scala , 1 e 9, che significano “molto simile” e “molto dissimile”, rispettivamente.
Una funzione che implementa l’MDS non metrico è isoMDS(), del package MASS.
## initial value 20.504211
## iter 5 value 15.216103
## iter 5 value 15.207237
## iter 5 value 15.207237
## final value 15.207237
## converged## [1] 15.20724L’applicazione qui sopra ha cercato la configurazione di miglior adattamento in un spazio con k = 2 dimensioni (valore predefinito).
Si ottiene così una configurazione il cui valore di Stress è pari a 15.21, che corrisponde ad un adattamento relativamente scarso.
Rappresentando graficamente la soluzione bidimensionale, possiamo vedere che i tre leader di ideologia fascista sono raggruppati tra loro, così come lo sono i tre primi ministri inglesi. Stalin e Mao Tse-Tung sono più isolati, rispetto agli altri leader. Eisenhower sembra più associato al governo inglese che al suo presidente Truman. La cosa più interesante, che è De Gaulle si posiziona al centro della soluzione MDS:
ds <- data.frame(V1=WWII_mds$points[, 1],
V2= WWII_mds$points[, 2],
label = attr(wwiileaders, "Labels"))
ggp <- ggplot(data = ds, mapping = aes(x=V1, y = V2, label=label)) +
geom_point() +
geom_text(hjust = 0.5, vjust = -0.5) +
xlab("Prima dimensione") + ylab("Seconda dimensione") +
coord_fixed(ratio = 1, xlim = c(-6, 6), ylim = c(-6, 6))
print(ggp)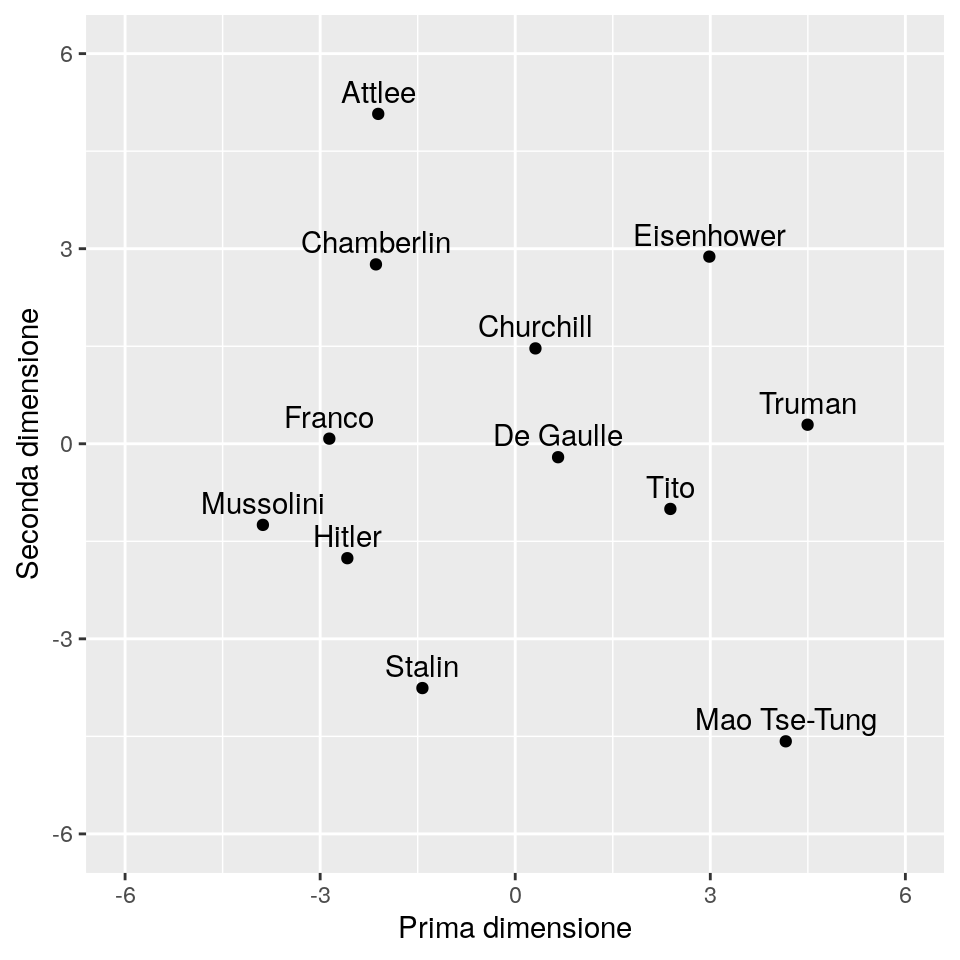
La qualità di un MDS può essere valutata in maniera informale tracciado in uno scatterplot le dissimilarià originali e le distanze ottenute dall’MDS, ottenendo il cosiddetto diagramma di Shepard. In una situazione ideale, i punti dovrebbero ricadere sulla bisettrice del primo quadrante. Nel nostro caso, sono abbastanza evidenti discostamenti:
WWII_shep <- as.data.frame(Shepard(wwiileaders, WWII_mds$points))
ggp <- ggplot(WWII_shep, aes(x = WWII_shep[, 1], y = WWII_shep[, 2])) +
geom_point(size = 1) +
geom_step(aes(y = WWII_shep[, 3])) +
xlab("Osservate") + ylab("Adattate") +
ggtitle("Diagramma di Shepard")
print(ggp)
Per migliorare il modello possiamo provare a calcolare il valore di Stress per diverse soluzioni MDS (\(k\)):
ndim <- 1:7
stress_mds <- sapply(ndim, function(i) isoMDS(wwiileaders, k = i,
trace = FALSE)$stress/100)
WWII_stress <- data.frame(Dimensioni = ndim, Stress = stress_mds)
ggp <- ggplot(WWII_stress, aes(x = Dimensioni, y = Stress)) +
geom_point() +
geom_line() +
scale_y_continuous(limits = c(0, max(stress_mds)),
breaks = seq(0, max(stress_mds), by = .05)) +
scale_x_continuous(limits = c(0, max(ndim)), breaks = ndim)
print(ggp)
Sembra che una soluzione discreta si possa avere con 3 dimensioni. Proviamo a vederne una rappresentazione grafica:
## initial value 14.418825
## iter 5 value 10.271773
## iter 10 value 9.992507
## final value 9.976593
## convergedpanel.txt <- function(x, y, ...) {
points(x, y, ...)
text(x, y, labels = rownames(WWII_final), pos = 1, cex = .8, offset = .5)
}
pairs(x = WWII_final, panel = panel.txt, xlim = c(-5, 5), ylim = c(-5, 5))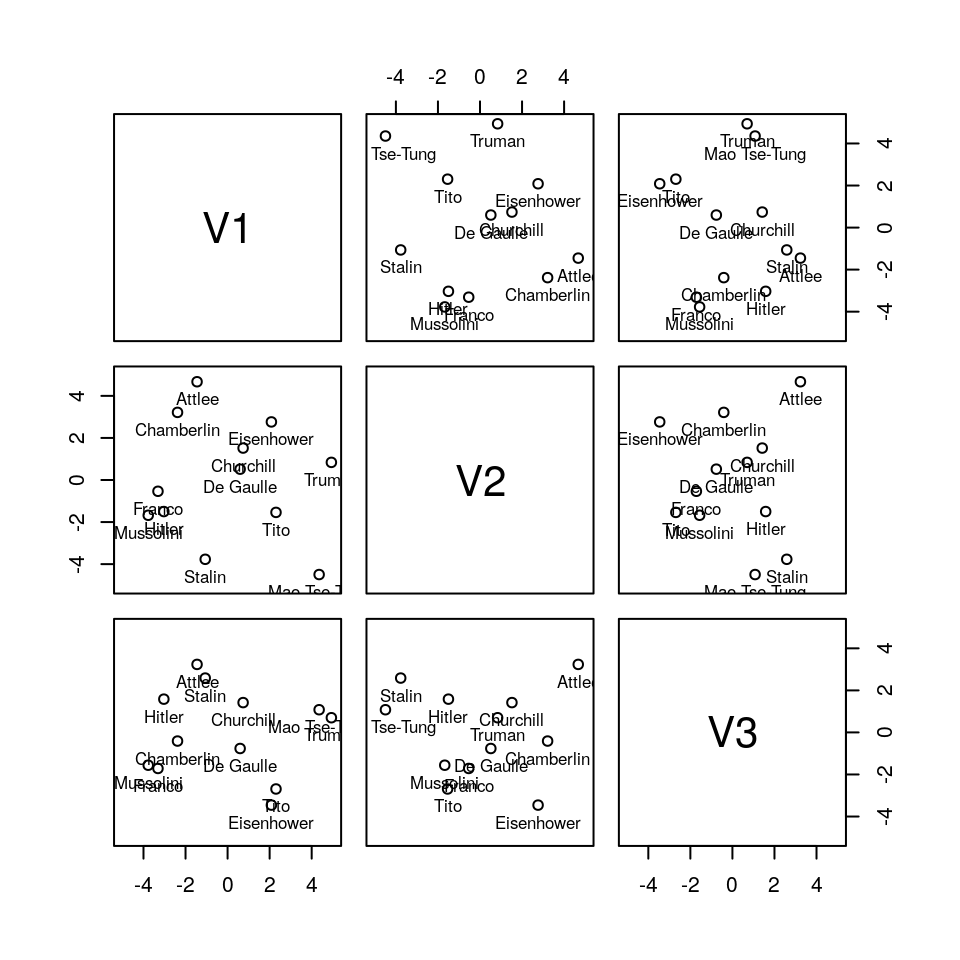
Quallo che segue, invece, è il codice per ottenere un grafico 3D per le tre dimensioni:
3.4 Altri Algoritmi di MDS
3.4.1 Sammon Mapping (mappatura di Sammon)
Un altro approccio popolare, usato principalmente nel machine learning per scopi di pattern recognition, è la mappatura non lineare di Sammon. Questo è considerato un approccio non lineare poiché la mappatura non può essere rappresentata come una combinazione lineare delle variabili originarie, come fatto, per esempio, con l’analisi delle componenti principali (PCA). La mappatura di Sammon è ottenuta pesando le differenze quadratiche tra distance osservate e adattate con l’inverso delle distance osservate. Come conseguenza, il Sammon mapping preserva le distance osservate piccole, dando loro una maggiore importanza rispetto alle distanze più grandi nella procedura di fitting.
Il mapping non lineare di Sammon può essere usato sia per dati metrici che per dati non metrici.
La funzione sammon() disponibile nel package MASS implementa solo la variante non metrica
dell’algoritmo di Sammon.
3.4.2 Il package smacof
Nel package smacof del CRAN (si veda de Leeuw, J. and Mair, P. (2009), Multidimensional Scaling Using
Majorization: SMACOF in R, Journal of Statistical Software, 31, 3, 1-30)
sono disponibili molte altre varianti di MDS
. The package fornisce i seguenti metodi di MDS:
smacofSym(): MDS semplice su una matrice di dissimilarità simmetrica,smacofIndDiff(): MDS per scaling su differenze individuali (MDS 3-way),smacofRect(): modelli di unfolding,smacofConstraint(): MDS confermativo,smacofSphere.primal()esmacofSphere.dual(): MDS sferico.
3.5 Alcuni cenni di teoria
Un algoritmo di MDS è finalizzato a posizionare ogni oggetto in uno spazio \(K\)-dimensionale tale per cui le distanze originarie tra oggetti siano mantenute meglio possibile.
I dati da analizzare sono una raccolta di \(N\) oggetti, su uno spazio \(P\)-dimensionale (una matrice \(X_{N \times P}\)), su cui è definita una funzione di distanza (o dissimilarità):
\(\delta_{i,j}\)= distanza tra l’oggetto \(i\) e l’oggetto \(j\).
Queste distanze (o dissimilarità) sono valori di una matrice di dissimilarità:
\[ \Delta=\begin{bmatrix} \delta_{1,1}& \delta_{1,2} & \cdots & \delta_{1,N} \\ \delta_{2,1}& \delta_{2,2} & \cdots & \delta_{2,N} \\ \cdots & \cdots & \cdots & \cdots \\ \delta_{N,1}& \delta_{N,2} & \cdots & \delta_{N,N} \end{bmatrix} \]
L’obiettivo dell’MDS è, dato \(\Delta\), trovare \(N\) vettori \(\underline{x}_1,\ldots,\underline{x}_N \in \mathbb{R}^K\), con \(K<P\), e usualmente \(K=2\) o \(K=3\), tali che
\(\|\underline{x}_i - \underline{x}_j\| \approx \delta_{i,j}\) per ogni \(i,j\in {1,\dots,N}\), dove \(\|\cdot\|\) è una norma vettoriale. Nell’MDS classico, questa norma è la distanza euclidea ma, in un senso più ampio, può essere una metrica o una distanza arbitraria, o una funziona di similarità (somiglianza).
In altre parole, MDS tenta di trovare “embedding” (un “incorporamento”) degli \(N\) oggetti in \(\mathbb{R}^K\) tali per cui le distanze tra gli oggetti si mantengano. Se la dimensione \(K\) è scelta pari a 2 o 3, possiamo tracciare i vettori \(x_i\) per ottenere una visualizzazione delle similarità degli \(N\) oggetti. Si noti che i vettori \(x_i\) sono generalmente non unici: con la distanza euclidea, possono essere traslati, ruotati o riflessi arbitrariamente, poiché queste trasformazioni non modificano le distanze a coppie \(\|\underline{x}_i - \underline{x}_j\|\).
Ci sono diversi approcci per determinare i vettori \(x_i\). Usualmente, MDS è formulato come un problema di ottimizzazione, dove si trovavano i \((\underline{x}_1,\ldots,\underline{x}_N)\) come vettori che minimizzano una qualche funzione di costo, per esempio:
\(\min_{\underline{x}_1,\ldots,\underline{x}_N} \sum_{i<j} ( \|\underline{x}_i - \underline{x}_j\| - \delta_{i,j} )^2. \,\)
Si può quindi cercare una soluzione usando una qualche tecnica di ottimizzazione numerica.
3.5.1 MDS metrico
Per alcune funzioni di distanza e di costo particolari (per es., quando si usa l’MDS metrico con distanze euclidee), la matrice di distanze quadrata può essere calcolata come: \[ \Delta = D(X) = diag(X X^T) \underline{1}^T + \underline{1} diag(XX^T)^T − 2XX^T \]
e se si applica una centratura dei dati \(X\) tramite \(L \cdot D\), dove \(L=(I − \underline{1} \underline{1}^T )\), si può dimostrare che: \[ D(X)=D(LX) \] In altre parole, le distanze sono invarianti a traslazioni (come già detto). Inoltre, data una matrice di distanze \(\Delta\) derivante da una matrice di dati \(X\), si può dimostrare che: \[ - L \Delta L = 2 L X X^T L \]
In questo caso, i “minimizzatori” della funzione di costo possono essere individuati analiticamente in termini di decomposizioni in autovalori di: \[ -1/2 \cdot L \Delta L = \Gamma \Lambda \Gamma^T \] dove \(\Gamma\) è una matrice ortogonale \((P \times K)\), e \(\Lambda\) è una matrice diagonale \((K \times K)\) dei primi \(K\) autovalori più grandi in ordine decrescente.
I punti (righe) della matrice \(Z\) \((N \times K)\): \[ Z = \Gamma \Lambda^{1/2} \] rappresentano una proiezione delle righe di \(LX\) in un sottospazio di dimensioni inferiori che preserva gran parte delle distanze, e quindi è una soluzione del precedente problema di ottimo.
3.5.2 MDS non metrico
A differenza dell’MDS metrico, MDS non metrico (isoMDS) ricerca sia una relazione monotona non parametrica tra le dissimilarità nella matrice degli item e le distanze euclidee tra item, sia la posizione di ogni item nello spazio di dimensionalità inferiore.
MDS non è più una procedure esatta quanto un modo per “riarrangiare” oggetti in maniera efficiente, tramite un algoritmo iterativo, in modo tale da giungere ad una configurazioneche meglio approssima le distanze osservate.
La procedura in effetti sposta gli oggetti in \(R^K\), dove \(K<P\), e controlla quanto le distanze tra gli oggetti possano essere ben riprodotte con la nuova configurazione. In in termini più tecnici, usa un algoritmo di minimizzazione di funzioni che valuta diverse configurazioni con l’obiettivo di minimizzare la “mancanza di adattamento” (“lack of fit”).
La misura di mancanza di adattamento è chiamata Stress.
Il valore di stress usato in isoMDS() per una configurazione è definito da:
\[ Stress = \dfrac{\sum_{i,j}{\left(d_{i,j} - \delta_{i,j} \right)^2}}{\sum_{i,j} d_{i,j}^2} \]
Nella formula qui sopra, \(d_{i,j}\) indica le distanze riprodotte, dato il rispettivo numero di dimensioni, e \(\delta_{i,j}\) indica le distanze osservate. In ogni modo, le distanze di input possono subire qualunque trasformazione monotòna.